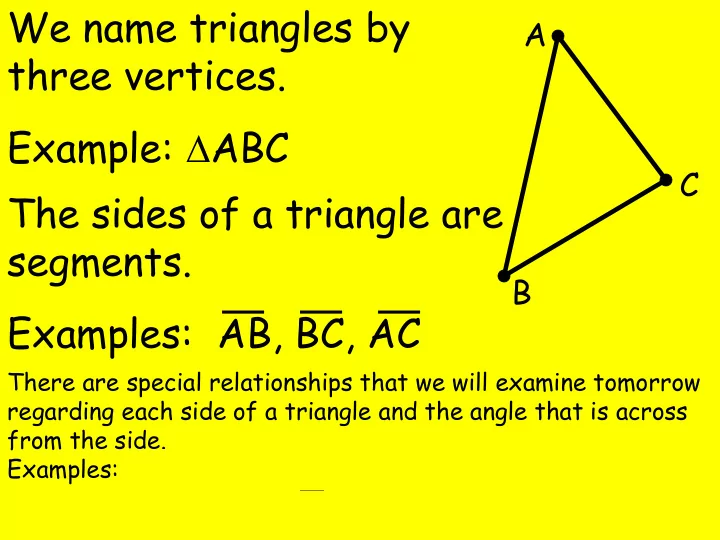
We name triangles by A three vertices. Example: ABC C The sides - PowerPoint PPT Presentation

We name triangles by A three vertices. Example: ∆ ABC C The sides of a triangle are segments. B Examples: AB, BC, AC There are special relationships that we will examine tomorrow regarding each side of a triangle and the angle that is across from the side. Examples: AB is across from  C AC is across from  B BC is across from  A

Classifying Triangles – By Angles Acute Triangle – A Equiangular Triangle – A triangle with three acute triangle with three angles. congruent angles. 70° 60° 50° Obtuse Triangle – A triangle Right Triangle – A triangle with one obtuse angle. with one right angle. 105°

Classifying Triangles – By Sides Scalene Triangle – A triangle with no congruent sides. Isosceles Triangle – A Equilateral Triangle – A triangle with two triangle with three congruent sides. congruent sides.

Theorem – the angle measures in a triangle sum to 180. A B 4 5 2 1 3 D C Given: AB // DC Prove: m  1 + m  2 + m  3 = 180

A B Given: AB // DC 4 5 2 Prove: m  1 + m  2 + m  3 = 180 1 3 D C 1. AB // DC 1. Given 2. If lines are parallel, then 2. m  1 = m  4; alternate interior angles are m  3 = m  5 congruent. 3. Angle Addition Postulate 3. m  ABC = m  4 + m  2 4. Angle Addition Postulate 4. m  ABC + m  5 = 180. 5. m  4 + m  2 + m  5 = 180 5. Substitution 6. m  1 + m  2 + m  3 = 180 6. Substitution

Algebra Connection m  A = 3(7.3) + 15 B m  A = 36.9 9 11 x  10 m  C = 9(7.3) – 2 3x + 15 9x - 2 m  C = 63.7 A C 9 3 x 15 9 x 2 11 x 180       10 9 m  B = 11(7.3) – 23 x 12 . 1 180   10 m  B = 79.4 23 x 167 . 9  Check: x  7 . 3 180 36.9 + 63.7 + 79.4 = ______

Corollary 1 – There can be at most one right angle or one obtuse angle in a given triangle.

Corollary 2 – The acute angles in a right triangle are complementary. 2 3 1 Given:  3 is a right angle. Prove:  1 and  2 are complementary

Given:  3 is a right angle. 2 3 1 Prove:  1 and  2 are complementary 1. Given 1.  3 is a right angle 2. Definition of a right angle 2. m  3 = 90 3. The angle measures in a 3. m  1 + m  2 + m  3 = 180 triangle sum to 180. 4. m  1 + m  2 + 90 = 180 4. Substitution 5. m  1 + m  2 = 90 5. Subtraction 6.  1 and  2 are 6. Definition of complementary complementary angles

m  1 = 135  6 45  m  2 = 5 m  3 = 60  2 3 4 m  4 = 120  1 m  5 = 75  m  6 = 105  1 m  3 + m  5 = m  ______ 6 m  2 + m  3 = m  ______ 4 m  2 + m  5 = m  ______

Theorem – The measure of an exterior angle of a triangle equals the sum of the measures of the two remote interior angles. 6 5 2 3 4 1 1 m  3 + m  5 = m  ______ 6 m  2 + m  3 = m  ______ 4 m  2 + m  5 = m  ______

B Given: D ABC 2 Prove: m  1 + m  2 = m  4 1 3 4 A C 1. Given 1. D ABC. 2. The angle measures in 2. m  1 + m  2 + m  3 = 180. a triangle sum to 180. 3. m  3 + m  4 = 180. 3. Angle Addition Postulate 4. m  1 + m  2 + m  3 = m  3 + m  4 4. Substitution 5. Subtraction 5. m  1 + m  2 = m  4 Property

Algebra Connection 3x - 1 35° 117° 82° 7x - 2 12x - 27 3x – 1 + 7x – 2 = 12x - 27 10x – 3 = 12x - 27 24 = 2x 12 = x

Algebra Connection 2y 130° 4x 2y + 90 = 130 4x + 130 = 180 4x = 50 2y = 40 x = 12.5 y = 20 Homework: p. 97 WE #1, 2, 5-13, 19, 20 draw all diagrams & 3.1-3.3 Quiz Review Part Three