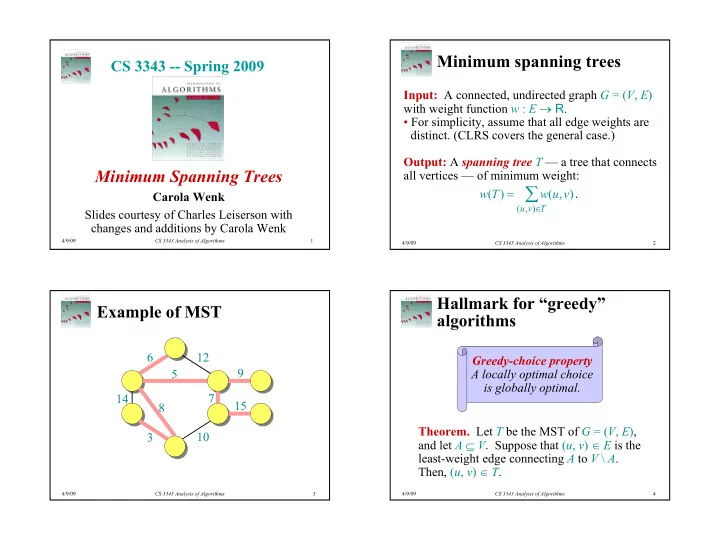

Minimum spanning trees CS 3343 -- Spring 2009 Input: A connected, undirected graph G = ( V , E ) with weight function w : E → R . • For simplicity, assume that all edge weights are distinct. (CLRS covers the general case.) Output: A spanning tree T — a tree that connects Minimum Spanning Trees all vertices — of minimum weight: ∑ = w ( T ) w ( u , v ) . Carola Wenk ∈ ( u , v ) T Slides courtesy of Charles Leiserson with changes and additions by Carola Wenk 4/9/09 CS 3343 Analysis of Algorithms 1 4/9/09 CS 3343 Analysis of Algorithms 2 Hallmark for “greedy” Example of MST algorithms 6 12 Greedy-choice property 9 5 A locally optimal choice is globally optimal. 14 7 15 8 Theorem. Let T be the MST of G = ( V , E ), 10 3 and let A ⊆ V . Suppose that ( u , v ) ∈ E is the least-weight edge connecting A to V \ A . Then, ( u , v ) ∈ T . 4/9/09 CS 3343 Analysis of Algorithms 3 4/9/09 CS 3343 Analysis of Algorithms 4 1
Proof of theorem Proof of theorem Proof. Suppose ( u , v ) ∉ T . Cut and paste. Proof. Suppose ( u , v ) ∉ T . Cut and paste. T : v T : v u u ∈ A ∈ A ( u , v ) = least-weight edge ( u , v ) = least-weight edge ∈ V \ A ∈ V \ A connecting A to V \ A connecting A to V \ A Consider the unique simple path from u to v in T . 4/9/09 CS 3343 Analysis of Algorithms 5 4/9/09 CS 3343 Analysis of Algorithms 6 Proof of theorem Proof of theorem Proof. Suppose ( u , v ) ∉ T . Cut and paste. Proof. Suppose ( u , v ) ∉ T . Cut and paste. T ′ : T : v v u u ∈ A ∈ A ( u , v ) = least-weight edge ( u , v ) = least-weight edge ∈ V \ A ∈ V \ A connecting A to V \ A connecting A to V \ A Consider the unique simple path from u to v in T . Consider the unique simple path from u to v in T . Swap ( u , v ) with the first edge on this path that Swap ( u , v ) with the first edge on this path that connects a vertex in A to a vertex in V \ A . connects a vertex in A to a vertex in V \ A . A lighter-weight spanning tree than T results. 4/9/09 CS 3343 Analysis of Algorithms 7 4/9/09 CS 3343 Analysis of Algorithms 8 2
Prim’s algorithm Example of Prim’s algorithm I DEA : Maintain V \ A as a priority queue Q . Key ∞ each vertex in Q with the weight of the least- ∈ A ∞ 6 12 weight edge connecting it to a vertex in A . ∈ V \ A 9 5 Q ← V ∞ ∞ ∞ ∞ ∞ ∞ key [ v ] ← ∞ for all v ∈ V 7 key [ s ] ← 0 for some arbitrary s ∈ V 14 15 8 while Q ≠ ∅ ∞ ∞ 0 ∞ ∞ 0 do u ← E XTRACT -M IN ( Q ) for each v ∈ Adj [ u ] 3 10 do if v ∈ Q and w ( u , v ) < key [ v ] ∞ ∞ u ← E XTRACT -M IN ( Q ) ⊳ D ECREASE -K EY then key [ v ] ← w ( u , v ) for each v ∈ Adj [ u ] π [ v ] ← u do if v ∈ Q and w ( u , v ) < key [ v ] then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY At the end, {( v , π [ v ])} forms the MST. π [ v ] ← u 4/9/09 CS 3343 Analysis of Algorithms 9 4/9/09 CS 3343 Analysis of Algorithms 10 Example of Prim’s algorithm Example of Prim’s algorithm ∞ ∞ ∈ A ∞ ∈ A ∞ 6 12 6 12 ∈ V \ A ∈ V \ A 9 9 5 5 ∞ ∞ ∞ ∞ 7 ∞ ∞ ∞ ∞ ∞ 7 ∞ 14 7 14 7 15 15 8 8 ∞ ∞ ∞ 15 0 0 ∞ ∞ ∞ 15 0 0 10 10 3 3 ∞ 10 ∞ 10 u ← E XTRACT -M IN ( Q ) u ← E XTRACT -M IN ( Q ) for each v ∈ Adj [ u ] for each v ∈ Adj [ u ] do if v ∈ Q and w ( u , v ) < key [ v ] do if v ∈ Q and w ( u , v ) < key [ v ] then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY π [ v ] ← u π [ v ] ← u 4/9/09 CS 3343 Analysis of Algorithms 11 4/9/09 CS 3343 Analysis of Algorithms 12 3
Example of Prim’s algorithm Example of Prim’s algorithm ∞ 12 ∈ A ∞ ∈ A 12 6 12 6 12 ∈ V \ A ∈ V \ A 9 9 5 5 ∞ 7 ∞ 5 7 9 ∞ 7 ∞ 5 7 9 7 7 14 14 15 15 8 8 ∞ 15 ∞ 15 0 0 ∞ 15 ∞ 15 0 0 3 10 3 10 10 10 10 10 u ← E XTRACT -M IN ( Q ) u ← E XTRACT -M IN ( Q ) for each v ∈ Adj [ u ] for each v ∈ Adj [ u ] do if v ∈ Q and w ( u , v ) < key [ v ] do if v ∈ Q and w ( u , v ) < key [ v ] then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY π [ v ] ← u π [ v ] ← u 4/9/09 CS 3343 Analysis of Algorithms 13 4/9/09 CS 3343 Analysis of Algorithms 14 Example of Prim’s algorithm Example of Prim’s algorithm 12 6 ∈ A 12 ∈ A 6 6 12 6 12 ∈ V \ A ∈ V \ A 9 9 5 5 5 7 9 5 7 9 5 7 9 5 7 9 14 7 14 7 15 15 8 8 ∞ 15 14 15 0 0 ∞ 15 14 15 0 0 10 10 3 3 10 8 10 8 u ← E XTRACT -M IN ( Q ) u ← E XTRACT -M IN ( Q ) for each v ∈ Adj [ u ] for each v ∈ Adj [ u ] do if v ∈ Q and w ( u , v ) < key [ v ] do if v ∈ Q and w ( u , v ) < key [ v ] then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY π [ v ] ← u π [ v ] ← u 4/9/09 CS 3343 Analysis of Algorithms 15 4/9/09 CS 3343 Analysis of Algorithms 16 4
Example of Prim’s algorithm Example of Prim’s algorithm 6 6 ∈ A 6 ∈ A 6 6 12 6 12 ∈ V \ A ∈ V \ A 9 9 5 5 5 7 9 5 7 9 5 7 9 5 7 9 7 7 14 14 15 15 8 8 14 15 14 15 0 0 14 15 14 15 0 0 3 10 3 10 8 8 8 8 u ← E XTRACT -M IN ( Q ) u ← E XTRACT -M IN ( Q ) for each v ∈ Adj [ u ] for each v ∈ Adj [ u ] do if v ∈ Q and w ( u , v ) < key [ v ] do if v ∈ Q and w ( u , v ) < key [ v ] then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY π [ v ] ← u π [ v ] ← u 4/9/09 CS 3343 Analysis of Algorithms 17 4/9/09 CS 3343 Analysis of Algorithms 18 Example of Prim’s algorithm Example of Prim’s algorithm 6 6 ∈ A 6 ∈ A 6 6 12 6 12 ∈ V \ A ∈ V \ A 9 9 5 5 5 7 9 5 7 9 5 7 9 5 7 9 14 7 14 7 15 15 8 8 3 15 3 15 0 0 3 15 3 15 0 0 10 10 3 3 8 8 8 8 u ← E XTRACT -M IN ( Q ) u ← E XTRACT -M IN ( Q ) for each v ∈ Adj [ u ] for each v ∈ Adj [ u ] do if v ∈ Q and w ( u , v ) < key [ v ] do if v ∈ Q and w ( u , v ) < key [ v ] then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY π [ v ] ← u π [ v ] ← u 4/9/09 CS 3343 Analysis of Algorithms 19 4/9/09 CS 3343 Analysis of Algorithms 20 5
Example of Prim’s algorithm Example of Prim’s algorithm 6 6 ∈ A 6 ∈ A 6 6 12 6 12 ∈ V \ A ∈ V \ A 9 9 5 5 5 7 9 5 7 9 5 7 9 5 7 9 7 7 14 14 15 15 8 8 3 15 3 15 0 0 3 15 3 15 0 0 3 10 3 10 8 8 8 8 u ← E XTRACT -M IN ( Q ) u ← E XTRACT -M IN ( Q ) for each v ∈ Adj [ u ] for each v ∈ Adj [ u ] do if v ∈ Q and w ( u , v ) < key [ v ] do if v ∈ Q and w ( u , v ) < key [ v ] then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY then key [ v ] ← w ( u , v ) ⊳ D ECREASE -K EY π [ v ] ← u π [ v ] ← u 4/9/09 CS 3343 Analysis of Algorithms 21 4/9/09 CS 3343 Analysis of Algorithms 22 Analysis of Prim Analysis of Prim (continued) Q ← V Time = Θ (| V| )· T E XTRACT- M IN + Θ (| E| )· T D ECREASE- K EY Θ (| V| ) key [ v ] ← ∞ for all v ∈ V total key [ s ] ← 0 for some arbitrary s ∈ V Q T E XTRACT- M IN T D ECREASE- K EY Total while Q ≠ ∅ do u ← E XTRACT -M IN ( Q ) array O (| V| ) O (1) O (| V| 2 ) for each v ∈ Adj [ u ] | V | degree ( u ) do if v ∈ Q and w ( u , v ) < key [ v ] times binary times then key [ v ] ← w ( u , v ) O (log | V| ) O (log | V| ) O (| E| log | V| ) heap π [ v ] ← u Fibonacci O (log | V| ) O (1) O (| E| + | V| log | V| ) Handshaking Lemma ⇒ Θ (| E| ) implicit D ECREASE -K EY ’s. heap amortized amortized worst case Time = Θ (| V| )· T E XTRACT- M IN + Θ (| E| )· T D ECREASE- K EY 4/9/09 CS 3343 Analysis of Algorithms 23 4/9/09 CS 3343 Analysis of Algorithms 24 6
Kruskal’s algorithm Example of Kruskal’s algorithm I DEA (again greedy) : S={ {a},{b},{c},{d},{e} Repeatedly pick edge with smallest weight as long as it MST edges a a {f},{g},{h} } 6 12 does not form a cycle. a set repr. 9 5 b c d • The algorithm creates a set of trees (a forest ) b c d • During the algorithm the added edges merge the 7 14 15 trees together, such that in the end only one tree 8 e f g e f g remains 3 10 • The correctness of this greedy strategy is not obvious h h and needs to be proven. (Proof skipped here.) Every node is a single tree. 4/9/09 CS 3343 Analysis of Algorithms 25 4/9/09 CS 3343 Analysis of Algorithms 26 Example of Kruskal’s algorithm Example of Kruskal’s algorithm S={ {a},{b},{c},{d},{f} S={ {a},{d},{f}, {g} MST edges a MST edges a a a {g}, {e, h} } {e, h}, {b, c} } 6 12 6 12 a set repr. a set repr. 9 9 5 5 b c d b c d b c d b c d 14 7 14 7 15 15 8 8 e f g e f g e f g e f g 10 10 3 3 h h h h Edge 3 merged two singleton trees. 4/9/09 CS 3343 Analysis of Algorithms 27 4/9/09 CS 3343 Analysis of Algorithms 28 7
Recommend
More recommend