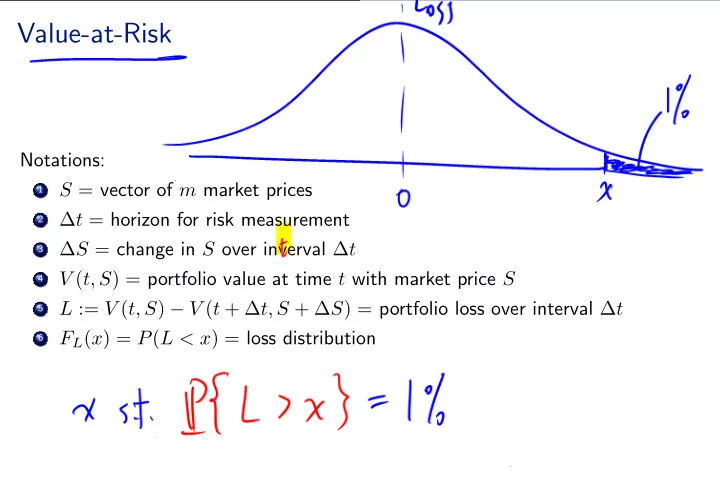
Value-at-Risk Notations: . S = vector of m market prices 1 . t = - PowerPoint PPT Presentation

Value-at-Risk Notations: . S = vector of m market prices 1 . ∆ t = horizon for risk measurement 2 . ∆ S = change in S over inverval ∆ t 3 . V ( t, S ) = portfolio value at time t with market price S 4 . L := V ( t, S ) − V ( t + ∆ t, S + ∆ S ) = portfolio loss over interval ∆ t 5 . F L ( x ) = P ( L < x ) = loss distribution 6 . .

Value-at-Risk A few remarks: VaR is a measure of risk, but also reflects the sufficient capital to sustain large losses. The interval ∆ t is typically quite short, e.g. 2 weeks for banks, as required by regulators. For fund management, the horizon is directly linked to the underlying assets (e.g. long/short term derivatives). For risk management purposes, it’s important to understand the sensitivies of VaR (or other risk measures) w.r.t time and underlying asset prices. . .

Linear Portfolio under Multivariate Normal Distribution The simplest approach to VaR is to consider the change in value ∆ V = δ T ∆ S, for some vector of sensitivies δ . Assume ∆ S ∼ N (0 , Σ S ) for some covariance matrix Σ S . L = δ T Σ S δ (a scalar). Since L = − ∆ V ∼ N (0 , σ 2 L ) , where σ 2 E.g. the 99% VaR is 2 . 33 σ L (note: Φ(2 . 33) = 0 . 99 ). Here, we’re assuming a very small ∆ t . . .

Delta-Gamma Approximation To capture nonlinear dependence of loss on underlying prices, we incorporate a 2nd-order sensitivity term. By Taylor expansion, we derive the delta-gamma (quadratic) approximation: ∆ V ≈ ∂V ∂t ∆ t + δ T ∆ S + 1 2∆ S T Γ∆ S, where ∂ 2 V δ i = ∂V , Γ ij = ∂S i ∂S i ∂S j are the 1st and 2nd derivatives of V . Again, we’re assuming a small ∆ t . E.g. if V is the value of a European call on a stock S , then δ is the Delta and Γ is the Gamma of the option. . .

MC Simulation of Loss Probabilities In its simplest form, the MC simulation algorithm consists for the main steps: . Generate a vector of market moves ∆ S (via Z ) 1 . Compute portfolio loss − ∆ V . 2 . Estimate loss probability using 3 n 1 ∑ 1 { L i >x } n i =1 where L i is the i th sample loss. The computation of portfolio value and thus its loss may be complicated and computationally expensive. The delta-gamma approximation can help accelerate the simulation. It also provides insights for variance reduction. . .

Approximating Loss Distribution We suppose that ∆ S ∼ N (0 , Σ S ) , and express it in terms of indep. normals ∆ S = CZ, with Z ∼ N (0 , I ) . For this to hold, we need to choose CC T = Σ S . The delta-gamma approximation of loss L = − ∆ V is L ≈ a − ( C T δ ) T Z − 1 a = − ∆ t∂V 2 Z T ( C T Γ C ) Z, ∂t . .

Approximating Loss Distribution To simplify the last term, we choose a C as follows: C T = Σ S . Obtain ˜ C from Cholesky factorization, s.t. ˜ C ˜ C T Γ ˜ 2 ˜ The symmetric matrix − 1 C admits diagonalization: C T Γ ˜ C = U Λ U T , where Λ is a diagonal matrix with filled with the 2 ˜ − 1 eigenvalues λ i , and U is an orthogonal matrix ( UU T = I ) of eigenvectors. CU . Then, CC T = ˜ CUU T ˜ C T = Σ S . Take C = ˜ 2 C T Γ C = 1 2 U T ( ˜ C T Γ ˜ C ) U = U T ( U Λ U T ) U = Λ ← diagonal. Also, − 1 . .

Approximating Loss Distribution As a result, setting b = − C T δ , we have m ∑ L ≈ a + b T Z + Z T Λ Z = a + ( b j Z j + λ j Z 2 j ) ≡ Q. j =1 Since the loss admits the approximation: m ∑ ( b j Z j + λ j Z 2 L ≈ a + j ) ≡ Q, j =1 the delta-gamma approximation yields the loss probability in terms of Q : P ( L > x ) ≈ P ( Q > x ) . . .

Importance Sampling First, we look at the delta-gamma approximaion again: m ∑ ( b j Z j + λ j Z 2 L ≈ a + j ) ≡ Q, j =1 Here, Z ’s are indep. standard normals, representing the sources of randomness. Since ∆ S = CZ , or Z = C − 1 ∆ S → Z is linearly related to ∆ S . Large losses would incur when . for j with b j > 0 , Z j is large and positive; 1 . for j with b j < 0 , Z j is large and negative; 2 . for j with λ j > 0 , Z 2 j is large and positive. 3 What does this mean to importance sampling? . for j with b j > 0 , assign a positive mean to Z j ; 1 . for j with b j < 0 , assign a negative mean to Z j ; 2 . for j with λ j > 0 , increase the variance of Z j . 3 . .

Exponential Twisting Recall Q = a + ∑ m j =1 ( b j Z j + λ j Z 2 j ) , which involves simulating standard normals. For any mean vector µ and covariance matrix Σ , the likelihood ratio relating the density of N ( µ, Σ) to N (0 , I ) is 2 Z T Z ) exp( − 1 dP (0 ,I ) dP ( µ, Σ) = ) . ( | Σ | − 0 . 5 exp 2 ( Z − µ ) T Σ − 1 ( Z − µ ) − 1 Hence, the loss probability can be expressed as   m ∑  = E (0 ,I ) [ ] P (0 ,I ) ( b j Z j + λ j Z 2  a + j ) > x 1 { Q>x } j =1 [ dP (0 ,I ) ] = E ( µ, Σ) dP ( µ, Σ) 1 { Q>x } . . .

Loss Probability for a Portfolio of Options Consider a portfolio of calls and puts on the same underlying S . i (resp. k p Denote k c i ) be the no. of call (reps. put) with strike K i and maturity T i . The portfolio value at time t is n m ∑ ∑ k c k p W t = i C BS ( S t ; K i , T i ) + i P BS ( S t ; K i , T i ) � �� � � �� � i =1 i =1 =: C i ( S t ) =: P i ( S t ) where C BS and P BS are the Black-Scholes price functions for calls and puts. We seek to estimate the loss probability P ( W t − W t +∆ t > x ) . Take t = 0 , the initial wealth is W 0 (constant) from the above equation. . .

Applying Delta-Gamma Approximation √ µ = µ − 0 . 5 σ 2 . For small ∆ t , assume ∆ S ≈ S 0 (ˆ µ ∆ t + σ ∆ tZ ) , with ˆ For each call option, the change in price is approximately ∂ 2 C ∆ C ≈ ∂C ∂t ∆ t + ∂C ∂S ∆ S + 1 ∂S 2 ∆ S 2 2 √ √ ∆ tZ ) + γ c 2 S 2 ∆ tZ ) 2 = θ c ∆ t + δ c S 0 (ˆ µ ∆ t + σ 0 (ˆ µ ∆ t + σ 2 Z 2 , ≈ b c 0 + b c 1 Z + b c where b c 0 = θ c ∆ t + δ c S 0 ˆ µ ∆ t √ b c 1 = δ c S 0 σ ∆ t 2 = γ c b c 2 σ 2 S 2 0 ∆ t The (call) Greeks θ c , δ c , and γ c depend on strike and expiration date. Similar calculations yield the approximation ∆ P ≈ b p 0 + b p 1 Z + b p 2 Z 2 , with appropriate constants b p 0 , b p 1 , b p 2 involving the (put) Greeks θ p , δ p , and γ p . . . 13 / 29

Approximating Change in Portfolio Value The portfolio loss is given by n m ∑ ∑ i ∆ C i − k c k p i ∆ P i W 0 − W ∆ t = − i =1 i =1 n m ∑ ∑ k c i ( b ci 0 + b ci 1 Z + b ci 2 Z 2 ) − k p i ( b pi 0 + b pi 1 Z + b pi 2 Z 2 ) ≈ − i =1 i =1 = h 0 + h 1 Z + h 2 Z 2 , with constant coefficients h 0 , h 1 , h 2 . . .

Exponential Twisting Let f ( z ) be the standard normal pdf. Let κ ( θ ) be the moment generating function of h 0 + h 1 Z + h 2 Z 2 : κ ( θ ) = E [ e θ ( h 0 + h 1 Z + h 2 Z 2 ) ] . Introduce a new function g ( z ) g ( z ) = e θ ( h 0 + h 1 z + h 2 z 2 ) · f ( z ) (1) κ ( θ ) e θh 0 ( θh 1 z + ( θh 2 − 0 . 5) z 2 ) √ = 2 πκ ( θ ) exp . (2) σ 2 = 1 / (1 − 2 θh 2 ) . Define ˆ . .

Exponential Twisting We re-write g by completing the square : e θh 0 ( θh 1 z + ( θh 2 − 0 . 5) z 2 ) g ( z ) = √ 2 πκ ( θ ) exp ( ) e θh 0 − 1 σ 2 ( z 2 − 2 θh 1 ˆ σ 2 z ) = √ 2 πκ ( θ ) exp 2ˆ ( ) = e θh 0 +0 . 5 θ 2 h 2 σ 2 1 ˆ − 1 σ 2 ( z − θh 1 ˆ σ 2 ) 2 √ exp 2ˆ 2 πκ ( θ ) ( ) 1 − 1 σ 2 ( z − θh 1 ˆ σ 2 ) 2 = √ σ exp 2ˆ 2 π ˆ σe θh 0 +0 . 5 θ 2 h 2 σ 2 . σ 2 , ˆ σ 2 ) 1 ˆ ⇒ g ∼ N ( θh 1 ˆ notice κ ( θ ) = ˆ In other words, g is indeed a normal pdf for any choice of θ . . .

Simulation Algorithm σ 2 , ˆ σ 2 ) of g . Generate N samples V i ’s from the distribution N ( θh 1 ˆ Calculate N 1 f ( V i ) ∑ 1 { W 0 − W ∆ t ( V i ) >x } N g ( V i ) i =1 where W ∆ t ( V i ) is computed by the portfolio value based on the i th sample V i . . .

Loss Probability of Credit Portfolios Suppose you have credit risk exposure on m different firms. Let Y i be the default indicator for firm i . Default probability of firm i : P ( Y i = 1) = p i . When firm i default, a constant loss of c i is incurred. Portfolio loss: L = ∑ m i =1 c i Y i . Simulation is a useful way to estimate the loss distribution, or loss probability P ( L > x ) esp. for models with dependent defaults. . .

Independent Defaults Recall (loss) L = ∑ m i =1 c i Y i , and (default prob.) P ( Y i = 1) = p i . If we assume defaults are independent, then loss L is a sum of indep. rv’s. The distribution of L is characterized by the moment generating function: ( ) p i e θc i + (1 − p i ) E [ e θL ] = Π m i =1 E [ e θc i Y i ] = Π m . i =1 For each firm i , we can define a new measure (distribution for Y i ) via exponential twisting: dP θ dP = exp ( θY i − ψ ( θ )) , ( p i e θ + (1 − p i ) ) where ψ i ( θ ) = log E [ e θY i ] = log . We can estimate each loss probability from the distribution P θ : P ( Y i = 1) = E θ [ dP 1 { Y i =1 } ] . dP θ . .

Independent Defaults Recall (loss) L = ∑ m i =1 c i Y i , and (default prob.) P ( Y i = 1) = p i . ( p i e θ + (1 − p i ) ) Differentiation of ψ i ( θ ) = log E [ e θY i ] = log gives p i e θ ψ ′ i ( θ ) = ( p i e θ + (1 − p i )) , but this is in fact the probability of default under the measure P θ because i ( θ ) = E [ e θY i Y i ] ψ ′ = E [ e θY i − ψ ( θ ) Y i ] E [ e θY i ] = E θ [ Y i ] = P θ ( Y i = 1) =: p i ( θ ) . . .