Vacuum$polariza1on$in$QED$ force$between$two$electrons$ + ! - PowerPoint PPT Presentation

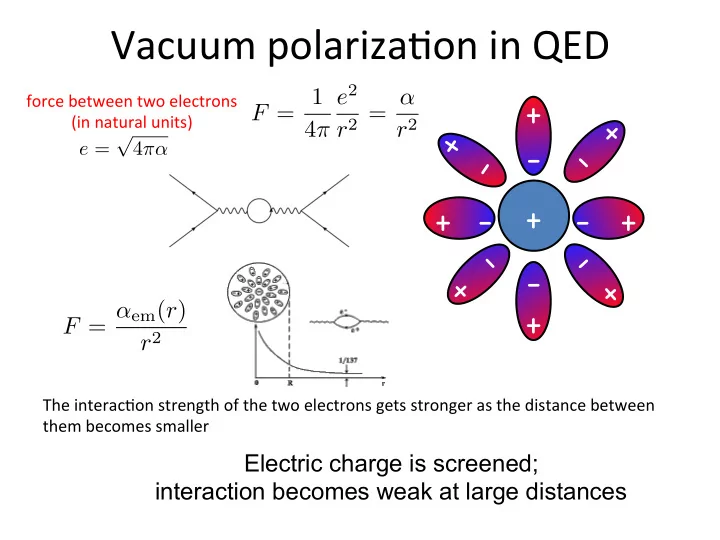
Vacuum$polariza1on$in$QED$ force$between$two$electrons$ + ! (in$natural$units)$ √ - ! e = 4 πα + ! + ! - ! - ! + ! - ! + ! The$interac1on$strength$of$the$two$electrons$gets$stronger$as$the$distance$between$ them$becomes$smaller$ Electric charge is screened; interaction becomes weak at large distances

Vacuum$polariza1on$in$QCD$ The left diagram is shared by QED and QCD which renders the interaction stronger at shorter distance (screening). The second diagram arising from the nonlinear interaction between gluons in QCD has the antiscreening effect, which makes the coupling weaker at short distance. • Color$is$an1Mscreened$ • Color$builds$up$away$from$a$source$ • Interac1on$becomes$strong$at$large$distances$(low$ momenta)$ • Confinement$of$quarks;$quarks$are$not$observed$as$ isolated$par1cles$

α s = g 2 Strong coupling constant 4 π In ¡quantum ¡field ¡theory, ¡the ¡coupling ¡constant ¡is ¡an ¡effec1ve ¡constant, ¡which ¡depends ¡on ¡ four-­‑momentum ¡ Q 2 ¡transferred. ¡For ¡strong ¡interac1ons, ¡the ¡ Q 2 ¡ dependence ¡ is ¡very ¡strong ¡ (gluons ¡-­‑ ¡as ¡the ¡field ¡quanta ¡-­‑ ¡ ¡carry ¡color ¡and ¡they ¡can ¡couple ¡to ¡other ¡gluons). ¡A ¡first-­‑ order ¡perturba1ve ¡QCD ¡calcula1on ¡(valid ¡at ¡very ¡large ¡ Q 2 ) ¡gives: ¡ running coupling 12 π α s Q 2 ( ) = ) ⋅ ln Q 2 / Λ QCD constant! ( ) ( 2 22 − 2 n f n f =6 − number of quark flavors Λ QCD − a parameter in QCD (~0.22 GeV), an infrared cutoff " The ¡spa1al ¡separa1on ¡between ¡quarks ¡goes ¡as ¡ ! = ¡ Q 2 ¡ Therefore, ¡for ¡very ¡small ¡distances ¡and ¡high ¡values ¡of ¡ Q 2 , ¡the ¡inter-­‑quark ¡coupling ¡decreases, ¡ vanishing ¡asympto1cally. ¡In ¡the ¡limit ¡of ¡very ¡large ¡ Q 2 , ¡quarks ¡can ¡be ¡considered ¡to ¡be ¡ “ free ” ¡(asympto1c ¡freedom). ¡On ¡the ¡other ¡hand, ¡at ¡large ¡distances, ¡the ¡inter-­‑quark ¡coupling ¡ increases ¡so ¡it ¡is ¡impossible ¡to ¡detach ¡individual ¡quarks ¡from ¡hadrons ¡(confinement). ¡ ¡ Asympto1c ¡freedom ¡was ¡described ¡in ¡1973 ¡by ¡Gross, ¡Wilczek, ¡and ¡Politzer ¡(Nobel ¡Prize ¡ 2004). ¡

It ¡is ¡customary ¡to ¡quote ¡ α s ¡at ¡the ¡91 ¡GeV ¡energy ¡scale ¡(the ¡mass ¡of ¡the ¡Z ¡boson) ¡

Mesons ¡ quark wave function of the pion Consider ¡ π -­‑ ¡( t =1 ¡and ¡ t 0 =1). ¡The ¡only ¡possible ¡combina1on ¡is ¡ ¡ π − = ud In ¡general, ¡it ¡is ¡possible ¡to ¡find ¡several ¡linearly ¡independent ¡components ¡ corresponding ¡to ¡the ¡same ¡ t ¡and ¡ t 0 . ¡The ¡appropriate ¡combina1on ¡is ¡given ¡by ¡isospin ¡ coupling ¡rules. ¡Furthermore, ¡the ¡wave ¡func1on ¡must ¡be ¡an1symmetric ¡among ¡the ¡ quarks. ¡This ¡problem ¡is ¡similar ¡to ¡that ¡of ¡a ¡two-­‑nucleon ¡wave ¡func1on! ¡ π 0 = 1 τ − π − = 1 ( ) uu − dd 2 2 T =1 triplet: π + = − ud What ¡about ¡the ¡symmetric ¡combina1on? ¡ η 0 = 1 ( ) uu + dd T =0 singlet: 2 To ¡produce ¡heavier ¡mesons ¡we ¡have ¡to ¡introduce ¡excita1ons ¡in ¡the ¡quark-­‑ an1quark ¡system ¡or ¡invoke ¡s -­‑ ¡and ¡other ¡more ¡massive ¡quarks ¡ ¡

The lightest strange mesons are kaons or K-mesons. Since s-quark has zero isospin, kaons come in two doublets with t =1/2: { K + ( us ), K 0 ( ds ) } , { K − ( us ), K 0 ( ds ) } Y = A + S + C + B + T hypercharge Q = − t 0 + 1 2 Y the ¡SU(3) ¡symmetry ¡limit ¡is ¡met ¡for ¡massless ¡u,d,s ¡quarks ¡ π − ( ud ) + p ( uud ) → K 0 ( ds ) + Λ ( uds ) strangeness is conserved! Pseudoscalar mesons ! J total angular momentum ! ! ! ! S = ! s q + ! ! ℓ + ℓ J = S , s q orbital angular momentum ! S total spin S can be either 0 or 1. The mesons with the relative zero orbital angular momentum are lower in energy. For the pion, S =0, hence J =0. Consequently, pions are “ scalar ” particles. But what about their parity? The parity of the pion is a product of intrinsic parities of the quark (+1), antiquark (-1) and the parity of the spatial wave function is 1. Hence, the pion has negative parity: it is a pseudoscalar meson .

With ¡(u,d,s) ¡quarks, ¡one ¡can ¡construct ¡9 ¡pseudoscalar ¡mesons ¡(recall ¡our ¡earlier ¡ discussion ¡about ¡the ¡number ¡of ¡gluons!): ¡ 9 ¡(nonet)=8 ¡(octet)+1 ¡(singlet) ¡ Members ¡of ¡the ¡octet ¡transform ¡into ¡each ¡other ¡under ¡rota1ons ¡in ¡flavor ¡ space ¡(SU(3) ¡group!). ¡The ¡remaining ¡meson, ¡ η 0 , ¡forms ¡a ¡1-­‑dim ¡irrep. ¡ ¡ ( us ) 497.61 ¡ π 0 = 1 ( ds ) ( ) uu − dd 2 493.68 ¡ η 8 = 1 ( ) uu + dd − 2 ss 6 η 0 = 1 547.86 ¡ 134.98 ¡ ( ud ) ( ) uu + dd + ss ( du ) 3 139.57 ¡ In ¡reality, ¡since ¡the ¡SU 3 ¡(flavor) ¡symmetry ¡ 957.78 ¡ is ¡not ¡exact ¡one, ¡the ¡observed ¡mesons ¡are: ¡ ¡ ( su ) ( sd ) η = η 8 cos ϑ + η 0 sin ϑ η ' = − η 8 sin ϑ + η 0 cos ϑ ϑ - Cabibbo angle, ~11 o for pseudoscalar mesons masses ¡are ¡in ¡MeV/c 2 ¡ The ¡eta ¡was ¡discovered ¡in ¡pion-­‑nucleon ¡collisions ¡at ¡the ¡Bevatron ¡(LBNL) ¡in ¡1961 ¡at ¡a ¡ 1me ¡when ¡the ¡proposal ¡of ¡the ¡Eighvold ¡Way ¡was ¡leading ¡to ¡predic1ons ¡and ¡ discoveries ¡of ¡new ¡par1cles. ¡

Vector mesons Here ¡ S =1, ¡hence ¡ J =1. ¡They ¡have ¡nega1ve ¡parity. ¡The ¡vector ¡mesons ¡are ¡more ¡massive ¡than ¡ their ¡pseudoscalar ¡counterparts, ¡reflec1ng ¡the ¡differences ¡in ¡the ¡interac1on ¡between ¡a ¡ quark ¡and ¡an ¡an1quark ¡in ¡the ¡ S =0 ¡and ¡ S =1 ¡states. ¡ π = 1 − J ( us ) 896 ¡ ( ds ) 892 ¡ ρ 0 = 1 ( ) uu − dd 2 775 ¡ ( ud ) ω = 1 783 ¡ ( ) uu + dd ( du ) 2 775 ¡ ϕ = ss 1019 ¡ ( su ) ( sd )

Baryons (qqq) With ¡three ¡flavors, ¡one ¡can ¡construct ¡a ¡total ¡of ¡3×3×3=27 ¡baryons ¡ baryon singlet t = 0 Λ 1 = 1 Completely ¡asymmetric ¡under ¡flavor ¡ { } uds + dsu + sud − dus − usd − sdu rota1ons ¡ 6 The ¡color ¡and ¡flavor ¡wave-­‑func1ons ¡should ¡be ¡an1symmetric ¡and ¡thus ¡zero ¡orbital ¡ angular ¡momentum ¡and ¡spin-­‑1/2 ¡are ¡not ¡possible ¡if ¡the ¡wave-­‑func1ons ¡is ¡to ¡be ¡overall ¡ − J π = 1 Λ (1405) an1symmetric ¡as ¡required ¡by ¡Fermi–Dirac ¡sta1s1cs. ¡Hence, ¡ L =1 ¡ 2

baryon decuplet (ddd) (udd) (uud) (uuu) + π = 3 (dds) (uds) (uus) J 2 (dss) (uss) (sss) The ¡discovery ¡of ¡the ¡omega ¡baryon ¡was ¡a ¡great ¡triumph ¡for ¡the ¡quark ¡model ¡of ¡baryons ¡ since ¡it ¡was ¡found ¡only ¡aber ¡its ¡existence, ¡mass, ¡and ¡decay ¡products ¡had ¡been ¡predicted ¡ by ¡Murray ¡Gell-­‑Mann ¡in ¡1962. ¡It ¡was ¡discovered ¡at ¡Brookhaven ¡in ¡1964. ¡ ¡

baryon octet The ¡remaining ¡16 ¡baryons ¡constructed ¡from ¡ u -­‑, ¡ s -­‑, ¡and ¡ d -­‑quarks ¡have ¡mixed ¡symmetry ¡in ¡ flavor. ¡The ¡lower ¡energy ¡octet ¡contains ¡protons ¡and ¡neutrons ¡as ¡its ¡members. ¡The ¡wave ¡ func1ons ¡for ¡each ¡member ¡in ¡the ¡group ¡is ¡symmetric ¡under ¡the ¡combined ¡exchange ¡of ¡ flavor ¡and ¡intrinsic ¡spin ¡(the ¡quarks ¡are ¡an1symmetric ¡in ¡color!) ¡ 939.6 ¡ 938.3 ¡ (udd) (uud) (ddd) (uds) 1115.7 ¡ 1197.4 ¡ + J π = 1 (dds) (uus) 1189.4 ¡ 1192.5 ¡ 2 1321.3 ¡ 1314.9 ¡ (dss) (uss) 1 { ( ) p = 2 u ↑ u ↑ d ↓ + u ↑ d ↓ u ↑ + d ↓ u ↑ u ↑ 18 example: proton ( ) wave function − u ↑ u ↓ d ↑ + u ↑ d ↑ u ↓ + d ↑ u ↑ u ↓ ( ) } + u ↓ u ↑ d ↑ + u ↓ d ↑ u ↑ + d ↑ u ↓ u ↑

New relatives of the proton hEp://www.fnal.gov/pub/ferminews/ferminews02-­‑06-­‑14/selex.html ¡ ¡ Baryon ¡Supermul1plet ¡using ¡four-­‑quark ¡models ¡and ¡half ¡spin ¡ Two New Particles Enter the Fold http://physics.aps.org/synopsis-for/10.1103/PhysRevLett.114.062004

The Roper resonance [ N (1440)P 11 ] is the proton's first radial excitation. Its lower- than-expected mass owes to a dressed-quark core shielded by a dense cloud of pions and other mesons.