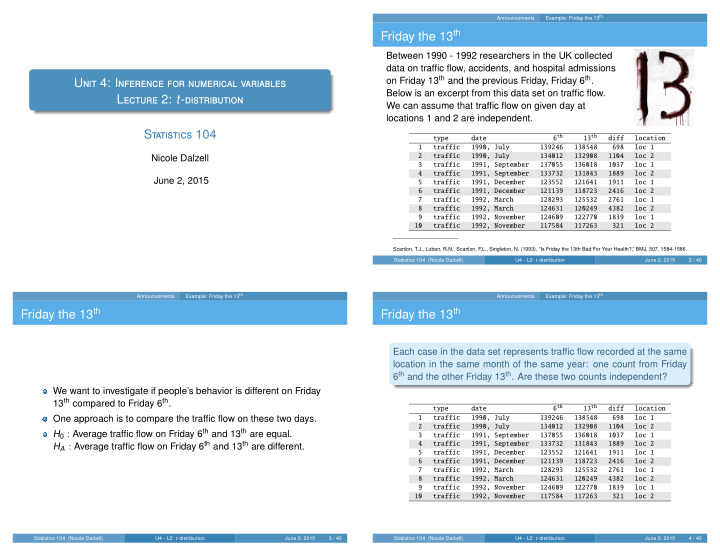



Example: Friday the 13 th Announcements Friday the 13 th Between 1990 - 1992 researchers in the UK collected data on traffic flow, accidents, and hospital admissions on Friday 13 th and the previous Friday, Friday 6 th . U 4: I Below is an excerpt from this data set on traffic flow. L 2: t - We can assume that traffic flow on given day at locations 1 and 2 are independent. S 104 6 th 13 th type date diff location 1 traffic 1990, July 139246 138548 698 loc 1 2 traffic 1990, July 134012 132908 1104 loc 2 Nicole Dalzell 3 traffic 1991, September 137055 136018 1037 loc 1 4 traffic 1991, September 133732 131843 1889 loc 2 June 2, 2015 5 traffic 1991, December 123552 121641 1911 loc 1 6 traffic 1991, December 121139 118723 2416 loc 2 7 traffic 1992, March 128293 125532 2761 loc 1 8 traffic 1992, March 124631 120249 4382 loc 2 9 traffic 1992, November 124609 122770 1839 loc 1 10 traffic 1992, November 117584 117263 321 loc 2 Scanlon, T.J., Luben, R.N., Scanlon, F .L., Singleton, N. (1993), “Is Friday the 13th Bad For Your Health?,” BMJ, 307, 1584-1586. Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 2 / 40 Example: Friday the 13 th Example: Friday the 13 th Announcements Announcements Friday the 13 th Friday the 13 th Each case in the data set represents traffic flow recorded at the same location in the same month of the same year: one count from Friday 6 th and the other Friday 13 th . Are these two counts independent? We want to investigate if people’s behavior is different on Friday 13 th compared to Friday 6 th . 6 th 13 th type date diff location One approach is to compare the traffic flow on these two days. 1 traffic 1990, July 139246 138548 698 loc 1 2 traffic 1990, July 134012 132908 1104 loc 2 H 0 : Average traffic flow on Friday 6 th and 13 th are equal. 3 traffic 1991, September 137055 136018 1037 loc 1 H A : Average traffic flow on Friday 6 th and 13 th are different. 4 traffic 1991, September 133732 131843 1889 loc 2 5 traffic 1991, December 123552 121641 1911 loc 1 6 traffic 1991, December 121139 118723 2416 loc 2 7 traffic 1992, March 128293 125532 2761 loc 1 8 traffic 1992, March 124631 120249 4382 loc 2 9 traffic 1992, November 124609 122770 1839 loc 1 10 traffic 1992, November 117584 117263 321 loc 2 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 3 / 40 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 4 / 40
Example: Friday the 13 th Example: Friday the 13 th Announcements Announcements Hypothesis Test Hypotheses Use these data to evaluate whether there is a difference in the traffic flow between Friday 6 th and 13 th . Participation question 6 th 13 th type date diff location What are the hypotheses for testing for a difference between the aver- 1 traffic 1990, July 139246 138548 698 loc 1 age traffic flow between Friday 6 th and 13 th ? 2 traffic 1990, July 134012 132908 1104 loc 2 3 traffic 1991, September 137055 136018 1037 loc 1 4 traffic 1991, September 133732 131843 1889 loc 2 (a) H 0 : µ 6 th = µ 13 th 5 traffic 1991, December 123552 121641 1911 loc 1 H A : µ 6 th � µ 13 th 6 traffic 1991, December 121139 118723 2416 loc 2 7 traffic 1992, March 128293 125532 2761 loc 1 (b) H 0 : p 6 th = p 13 th 8 traffic 1992, March 124631 120249 4382 loc 2 H A : p 6 th � p 13 th 9 traffic 1992, November 124609 122770 1839 loc 1 10 traffic 1992, November 117584 117263 321 loc 2 (c) H 0 : µ diff = 0 ↓ H A : µ diff � 0 ¯ x diff = 1836 (d) H 0 : ¯ x diff = 0 H A : ¯ x diff = 0 s diff = 1176 n = 10 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 5 / 40 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 6 / 40 Example: Friday the 13 th Announcements Small sample inference for the mean Conditions Review: what purpose does a large sample serve? Independence: We are told to assume that cases (rows) are independent. Sample size / skew: As long as observations are independent, and the population The sample distribution does not appear to be distribution is not extremely skewed, a large sample would ensure extremely skewed, but it’s very difficult to assess 5 that... 4 with such a small sample size. We might want to frequency 3 think about whether we would expect the population 2 the sampling distribution of the mean is nearly normal distribution to be skewed or not – probably not, it 1 s the estimate of the standard error, as √ n , is reliable 0 should be equally likely to have days with lower than 0 1000 2000 3000 4000 5000 Difference in traffic flow average traffic and higher than average traffic. n < 30 ! So what do we do when the sample size is small? We can use simulation, but when working with small sample means we can also use the t distribution. Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 7 / 40 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 8 / 40
Small sample inference for the mean The normality condition Small sample inference for the mean Introducing the t distribution The normality condition The t distribution When n is small, and the population standard deviation( σ ) is unknown (almost always), the uncertainty of the standard error estimate is addressed by using the t distribution . The CLT, which states that sampling distributions will be nearly This distribution also has a bell shape, but its tails are thicker normal, holds true for any sample size as long as the population than the normal model’s. distribution is nearly normal. Therefore observations are more likely to fall beyond two SDs While this is a helpful special case, it’s inherently difficult to verify from the mean than under the normal distribution. normality in small data sets. These extra thick tails are helpful for mitigating the effect of a We should exercise caution when verifying the normality less reliable estimate for the standard error of the sampling condition for small samples. It is important to not only examine distribution (since n is small) the data but also think about where the data come from. For example, ask: would I expect this distribution to be symmetric, normal and am I confident that outliers are rare? t −4 −2 0 2 4 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 9 / 40 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 10 / 40 Small sample inference for the mean Introducing the t distribution Small sample inference for the mean Evaluating hypotheses using the t distribution t test The t distribution (cont.) Use these data to evaluate whether there is a difference in the traffic flow between Friday 6 th and 13 th . Always centered at zero, like the standard normal ( z ) distribution. 6 th 13 th Has a single parameter: degrees of freedom ( df ). type date diff location 1 traffic 1990, July 139246 138548 698 loc 1 2 traffic 1990, July 134012 132908 1104 loc 2 3 traffic 1991, September 137055 136018 1037 loc 1 normal 4 traffic 1991, September 133732 131843 1889 loc 2 t, df=10 5 traffic 1991, December 123552 121641 1911 loc 1 t, df=5 6 traffic 1991, December 121139 118723 2416 loc 2 t, df=2 7 traffic 1992, March 128293 125532 2761 loc 1 t, df=1 8 traffic 1992, March 124631 120249 4382 loc 2 9 traffic 1992, November 124609 122770 1839 loc 1 10 traffic 1992, November 117584 117263 321 loc 2 ↓ −2 0 2 4 6 ¯ x diff = 1836 s diff = 1176 What happens to shape of the t distribution as df increases? n = 10 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 11 / 40 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 12 / 40
Small sample inference for the mean Evaluating hypotheses using the t distribution Small sample inference for the mean Evaluating hypotheses using the t distribution t statistic Degrees of Freedom s When estimating SE as √ n , and s is not a reliable estimate for σ (when n is small) we say that we “lose a degree of freedom”. Hence our calculations are penalized for working with data from a small Test statistic for inference on a small sample mean sample. The test statistic for inference on a small sample ( n < 30) mean is the T statistic with df = n − 1. normal T df = point estimate − null value t, df=10 SE t, df=5 t, df=2 t, df=1 Why is df = n − 1, i.e. what does it mean to lose a degree of freedom? −2 0 2 4 6 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 13 / 40 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 14 / 40 Small sample inference for the mean Evaluating hypotheses using the t distribution Small sample inference for the mean Evaluating hypotheses using the t distribution Using technology to find the p-value The p-value is, once again, calculated as the area tail area under the t distribution. Using R: > 2 * pt(4.94, df = 9, lower.tail = FALSE) [1] 0.0008022394 Using a web applet: http://www.socr.ucla.edu/htmls/SOCR Distributions.html Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 15 / 40 Statistics 104 (Nicole Dalzell) U4 - L2: t -distribution June 2, 2015 16 / 40
Recommend
More recommend