Type-checking on Heterogeneous Sequences in Common Lisp Jim Newton - PowerPoint PPT Presentation

Type-checking on Heterogeneous Sequences in Common Lisp Jim Newton EPITA/LRDE May 9, 2016 Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 1 / 31

Overview Introduction 1 Common Lisp Types Type Sequences 2 Limitations Rational Type Expression Generated Code Example: destructuring-case Overlapping Types Conclusion 3 Difficulties Encountered Summary Questions Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 2 / 31

Introduction Common Lisp Types Common Lisp Types Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 3 / 31

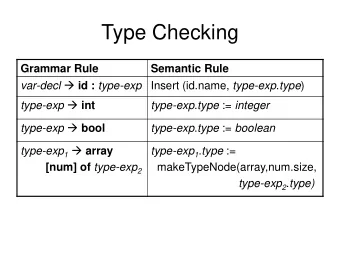
Introduction Common Lisp Types What is a type in Common Lisp? Definition (from CL specification) A (possibly infinite) set of objects. Definition (type specifier) An expression that denotes a type. Atomic examples t , integer , number , asdf:component Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 4 / 31

Introduction Common Lisp Types Type specifiers come in several forms. Compound type specifiers (eql 12) (member :x :y :z) (satisfies oddp) (and (or number string) (not (satisfies MY-FUN))) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 5 / 31

Introduction Common Lisp Types Type specifiers come in several forms. Compound type specifiers (eql 12) (member :x :y :z) (satisfies oddp) (and (or number string) (not (satisfies MY-FUN))) Specifiers for the empty type nil (and number string) (and (satisfies evenp) (satisfies oddp)) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 5 / 31

Introduction Common Lisp Types Using types with sequences Compile time (lambda (x y) (declare (type (vector float) x y)) (list x y)) Run time (typep my-list ’(cons t (cons t (cons string)))) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 6 / 31

Type Sequences Limitations Limitations Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 7 / 31

Type Sequences Limitations Limited capability for specifying heterogeneous sequences. You can’t specify the following. An arbitrary length, non-empty, list of floats: (1.0 2.0 3.0) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 8 / 31

Type Sequences Limitations Limited capability for specifying heterogeneous sequences. You can’t specify the following. An arbitrary length, non-empty, list of floats: (1.0 2.0 3.0) A plist such as: (:x 0 :y 2 :z 3) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 8 / 31

Type Sequences Rational Type Expression The Rational Type Expression Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 9 / 31

Type Sequences Rational Type Expression Introducing the RTE type Rational type expression vs. RTE type specifier number + (RTE (:+ number)) Example: (1.0 2.0 3.0) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 10 / 31

Type Sequences Rational Type Expression Introducing the RTE type Rational type expression vs. RTE type specifier number + (RTE (:+ number)) Example: (1.0 2.0 3.0) ( keyword · integer ) ∗ (RTE (:* (:cat keyword integer))) Example: (:x 0 :y 2 :z 3) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 10 / 31

Type Sequences Rational Type Expression Use RTE anywhere CL expects a type specifier. (typedef plist (type) ‘(and list (RTE (:* keyword ,type)))) (defun foo (A B) (declare (type (RTE (:+ number)) A) (type (plist float) B)) ...) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 11 / 31

Type Sequences Rational Type Expression An RTE can be expressed as a finite state machine. ( symbol · ( number + ∪ string + )) + (:+ symbol (:or (:+ number) (:+ string))) number number 2 symbol symbol 0 1 symbol string 3 string Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 12 / 31

Type Sequences Generated Code Generated Code Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 13 / 31

Type Sequences Generated Code State machine can be expressed in CL code (lambda (seq) (declare (optimize (speed 3) (debug 0) (safety 0))) (typecase seq (list ...) (simple-vector ...) (vector ...) (sequence ...) (t nil))) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 14 / 31

Type Sequences Generated Code Code generating implementing state machine number (tagbody 0 number 2 (unless seq (return nil)) (typecase (pop seq) (symbol (go 1)) symbol symbol 0 1 (t (return nil))) symbol 1 (unless seq (return nil)) string 3 (typecase (pop seq) (number (go 2)) (string (go 3)) string (t (return nil))) 2 3 (unless seq (return t)) (unless seq (return t)) (typecase (pop seq) (typecase (pop seq) (number (go 2)) (string (go 3)) (symbol (go 1)) (symbol (go 1)) (t (return nil))) (t (return nil))))) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 15 / 31

Type Sequences Example: destructuring-case destructuring-case Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 16 / 31

Type Sequences Example: destructuring-case Example of destructuring-case (destructuring-case DATA (typecase DATA ;; Case-1 ;; Case-1 ((a b &optional (c "")) ((rte (:cat integer (declare (type integer a) string (type string b c)) (:? string))) ...) ...destructuring-bind...) ;; Case-2 ;; Case-2 ((a (b c) ((rte ...complicated...) &key (x t) (y "") z ...destructuring-bind... &allow-other-keys) (declare (type fixnum a b c) (type symbol x) (type string y) (type list z)) ...)) ...)) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 17 / 31

Type Sequences Example: destructuring-case Regular type expression denoting Case-2 ( : cat ( : cat fixnum ( : and l i s t ( r t e ( : cat fixnum fixnum ) ) ) ) ( : and (: ∗ keyword t ) ( : cat (: ∗ ( not ( member : x : y : z ) ) t ) ( : or : empty − word ( : cat ( e q l : z ) fixnum (: ∗ ( not ( member : x : y )) t ) ( : ? ( e q l : y ) s t r i n g (: ∗ ( not ( e q l : x )) t ) ( : ? ( e q l : x ) symbol (: ∗ t t ) ) ) ) ( : cat ( e q l : z ) fixnum (: ∗ ( not ( member : x : y )) t ) ( : ? ( e q l : x ) symbol (: ∗ ( not ( e q l : y )) t ) ( : ? ( e q l : y ) s t r i n g (: ∗ t t ) ) ) ) ( : cat ( e q l : y ) s t r i n g (: ∗ ( not ( member : x : z ) ) t ) ( : ? ( e q l : z ) fixnum (: ∗ ( not ( e q l : x )) t ) ( : ? ( e q l : x ) symbol (: ∗ t t ) ) ) ) ( : cat ( e q l : x ) symbol (: ∗ ( not ( member : y : z ) ) t ) ( : ? ( e q l : z ) fixnum (: ∗ ( not ( e q l : y )) t ) ( : ? ( e q l : y ) s t r i n g (: ∗ t t ) ) ) ) ( : cat ( e q l : y ) s t r i n g (: ∗ ( not ( member : x : z )) t ) ( : ? ( e q l : x ) symbol (: ∗ ( not ( e q l : z ) ) t ) ( : ? ( e q l : z ) fixnum (: ∗ t t ) ) ) ) ( : cat ( e q l : x ) symbol (: ∗ ( not ( member : y : z )) t ) ( : ? ( e q l : y ) s t r i n g (: ∗ ( not ( e q l : z ) ) t ) ( : ? ( e q l : z ) fixnum (: ∗ t t ) ) ) ) ) ) ) ) Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 18 / 31

Type Sequences Example: destructuring-case Finite State Machine of Case-2 of destructuring-case T1 19 T20 20 T9 18 T6 T10 T17 8 T4 21 T1 T3 16 T21 T10 T4 7 9 T1 6 17 T8 T8 T3 T7 T3 0 1 2 T9 T6 T16 T19 3 4 23 5 T10 T1 T1 T10 22 25 T9 12 T1 11 T3 T6 T5 24 10 T4 T3 28 T8 T4 T15 T6 13 14 T9 T1 29 26 T8 T1 15 27 T18 Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 19 / 31

Type Sequences Overlapping Types Overlapping Types Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 20 / 31

Type Sequences Overlapping Types Rational type expression with overlapping types (( integer · number ) ∪ ( number · integer )) (:or (:cat integer number) (:cat number integer)) P 3 integer number P 0 P 1 number integer P 2 Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 21 / 31

Type Sequences Overlapping Types Overlapping types must decomposed into disjoint types (( integer · number ) ∪ (( number ∩ integer ) · integer )) (:or (:cat integer number) (:cat (and number (not integer)) integer)) P 3 integer number P 0 P 1 integer number ∩ integer P 2 Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 22 / 31

Type Sequences Overlapping Types Overlapping types considered harmful Disjoint Decomposed Set Expression A { 1 } A ∩ B ∩ C ∩ D ∩ F ∩ H { 2 } B ∩ C ∩ D C B 2 3 { 3 } B ∩ C ∩ D 4 { 4 } C ∩ B ∩ D 5 1 7 6 { 5 } B ∩ C ∩ D { 6 } B ∩ D ∩ C D { 7 } C ∩ D ∩ B F { 8 } D ∩ B ∩ C ∩ H 10 13 E { 9 } E 8 9 { 10 } F H { 11 } G G 12 11 { 12 } H ∩ D { 13 } D ∩ H ∩ E Jim Newton (EPITA/LRDE) Type-checking on Heterogeneous Sequences May 9, 2016 23 / 31