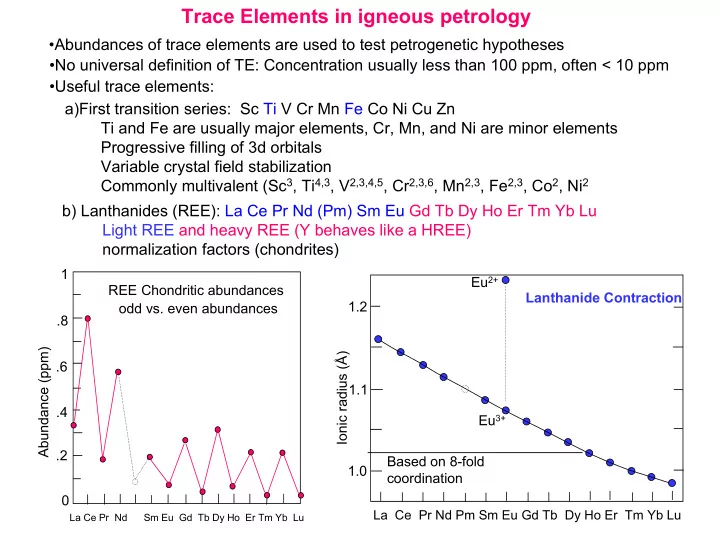
Trace Elements in igneous petrology Abundances of trace elements are - PowerPoint PPT Presentation

Trace Elements in igneous petrology •Abundances of trace elements are used to test petrogenetic hypotheses •No universal definition of TE: Concentration usually less than 100 ppm, often < 10 ppm •Useful trace elements: a)First transition series: Sc Ti V Cr Mn Fe Co Ni Cu Zn Ti and Fe are usually major elements, Cr, Mn, and Ni are minor elements Progressive filling of 3d orbitals Variable crystal field stabilization Commonly multivalent (Sc 3 , Ti 4,3 , V 2,3,4,5 , Cr 2,3,6 , Mn 2,3 , Fe 2,3 , Co 2 , Ni 2 b) Lanthanides (REE): La Ce Pr Nd (Pm) Sm Eu Gd Tb Dy Ho Er Tm Yb Lu Light REE and heavy REE (Y behaves like a HREE) normalization factors (chondrites) 1 Eu 2+ REE Chondritic abundances Lanthanide Contraction 1.2 odd vs. even abundances .8 Abundance (ppm) Ionic radius (Å) .6 1.1 .4 Eu 3+ .2 Based on 8-fold 1.0 coordination 0 La Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu La Ce Pr Nd Sm Eu Gd Tb Dy Ho Er Tm Yb Lu

(c) Large Ion Lithophile Elements (LILE): may also be partitioned into fluid phase Alkalis: K Rb Cs (monovalent) Alkaline earths: Ba Sr (divalent) Actinides: U, Th, Ra, Pa (multiple valency) (d) High field strength elements (HFSE): small, highly-charged ions Zr, Hf (4 valent) Nb, Ta (4 and 5 valent) (e) Chalcophile elements: Cu, Zn, Pb, Ag, Hg, PGE, (Fe, Co, Ni) (f) Siderophile elements: Fe, Ni, Co, Ge, P, Ga, Au (PGE)… • Decoupled from major elements: lack of stoichiometric constraints (not strictly true) • Goldschmidt’s Rules • Generalities: Incompatible elements are elements that tend to be excluded from common minerals (olivines, pyroxenes, garnets, feldspars, oxides…) in equilibrium with a melt, i.e., they have low D values. •Numerous exceptions, e.g., Sr, Eu in plag, Cr, Sc in pyroxene, Ni in olivine, HREE in garnet.. •Empirical (not thermodynamic) definition of D (see relevant definitions and equations posted on class website) C C i C / L D = i L C i C C / L D C where is the weight distribution coefficient, is concentration (ppm) of trace element i in liquid, and i i L C is concentration (ppm) of trace element i in the liquid i

For multiphase crystalline assemblages: = Bulk distribution coefficient of i between crystals and liquid = ∑ C / L D ij W D j i j W where is the weight fraction of mineral j in the solid assemblage j Trace elements are used to model processes of melting (equilibrium and fractional) and crystallization (equilibrium and fractional). To model melting processes, two types of melting are considered (1) modal melting where the minerals melt in the same proportions that they are present in the crystal assemblage and (2) non-modal melting in which the minerals melt in proportions controlled by the stoichiometry of the melting reaction, which usually has to be determined experimentally or from a known phase diagram. The equations for all types of crystallization and melting are listed on the class website under: “Trace element definitions and equations ”. C / L D Distribution coefficients i • Attempts have been made over the past 3 decades to determine the appropriate values of distribution coefficients to be used in modeling. The earliest attempts simply separated phenocrysts from matrix in volcanic rocks and analyzed each to obtain an empirical set of D values. Some of these data are still used today. • More recently experiments have been carried out over a wide range of T, P and X using a variety of methods. As the techniques of microanalysis of trace element abundances improved (SIMS, LA-ICPMS…), this approach has been popular.

D values are functions of T, P and composition of both crystalline and melt phases so the problem becomes one of controlling these variables and trying to establish a theoretical basis that would allow one to predict D values based on a limited number of experiments. Only limited success to date so a wide range of D values exist in the literature. Caveat: Be careful about choice of D values used—make sure they are appropriate. This figure on left shows D values for REE that have been used to model processes in mafic magmas. While the D values may vary as functions of T, P, X L and X xal , the figure clearly show the major differences among common minerals. Note the log scale on the Y-axis. The figure below shows an example of the effect on D values of changing crystal composition Good source of D values: Table 7.5 in the online book by W. M. White “Geochemistry”

Table 9-1 . Partition Coefficients (C S /C L ) for Some Commonly Used Trace Tables such as this one are useful Elements in Basaltic and Andesitic Rocks but they can also be misleading in Olivine Opx Cpx Garnet Plag Amph Magnetite that they imply that D values are Rb 0.010 0.022 0.031 0.042 0.071 0.29 constant for a given element in a Sr 0.014 0.040 0.060 0.012 1.830 0.46 given mineral Ba 0.010 0.013 0.026 0.023 0.23 0.42 14 7 0.01 Ni 5 0.955 6.8 29 30 0.01 Cr 0.70 10 34 1.345 2.00 7.4 Olivine/melt D values La 0.007 0.03 0.056 0.001 0.148 0.544 2 Rare Earth Elements Ce 0.006 0.02 0.092 0.007 0.082 0.843 2 Nd 0.006 0.03 0.230 0.026 0.055 1.340 2 20 Sm 0.007 0.05 0.445 0.102 0.039 1.804 1 D NI Eu 0.007 0.05 0.474 0.243 0.1/1.5* 1.557 1 Dy 0.013 0.15 0.582 1.940 0.023 2.024 1 Er 0.026 0.23 0.583 4.700 0.020 1.740 1.5 10 Yb 0.049 0.34 0.542 6.167 0.023 1.642 1.4 Lu 0.045 0.42 0.506 6.950 0.019 1.563 * Eu 3+ /Eu 2+ Italics are estimated Data from Rollinson (1993). 0 10 20 30 0 D values > 1 compatible element Wt. % MgO in liquid D values < 1 incompatible element This figure shows the range of values measured experimentally for the distribution coefficient of Ni in olivine showing the effect on D value of variable MgO content of the melt. There is also a temperature dependence which is “hidden” in these data. The experiments (>10 sets) were carried out at T ranging from 1600ºC to 1100ºC. Liquid compositions ranged from ultramafic (komatiites) to Table 9-1: from Winter (2001) An introduction to mafic (basalts). Igneous and metamorphic petrology. Prentice Hall

10 “Onuma” diagram for plagioclase In Onuma diagrams, partition coefficients plotted against ionic radius define smooth convex- Sr 2+ upward curves with a different Ca 2+ 1 curve for each valence. The D maximum in the curves predicts the best fit ionic radius. Ba 2+ 0.1 Ce 3+ Sm Mg 2+ Dy Lu Yb 0.01 1.0 1.2 1.6 0.8 1.4 Ionic radius (Å)

Normalization factors, spider diagrams, etc. 1. REE: REE abundances in minerals and rocks are normalized by dividing the abundances by abundances in C1 chondrites (see table below for typical values) Ch (ppm) This figure shows a typical REE La 0.325 normalized plot for basalts. In this Ce 0.798 example, basalts from the CRB flood Nd 0.567 basalt province. A pattern like this is Sm 0.186 said to show a moderate degree of Eu 0.0692 LREE enrichment (La/Yb) N > 1 Gd 0.255 Data from Hooper and Hawkesworth (1993) Tb 0.047 J. Petrol. , 34, 1203-1246. Reproduced in Dy 0.305 Winter (2001) An introduction to Igneous Er 0.209 and metamorphic petrology. Prentice Hall Yb 0.209 Lu 0.0349 2. Spidergrams: abundances of trace elements in minerals and rocks are normalized by dividing by abundances in the mantle (or MORB or…). Plotted in order of decreasing incompatibility Commonly used MORB-normalized spider diagram for normalization factors some representative analyses from for spider diagrams are the CRB flood basalts provided by Sun and McDonough (1989) Data from Hooper and Hawkesworth (1993) J. Petrol. , 34, 1203-1246. Reproduced in Winter (2001). An Introduction to Igneous and Metamorphic Petrology. Prentice Hall

Example of an equilibrium partial modal melting calculation involving Rb and Sr Suppose we are melting a lower crustal granulite containing 50% plagioclase + 25% cpx + 20% opx + 5% garnet and we want to track how the Rb, Sr and Rb/Sr concentrations in the melt vary as the melting progresses. Assuming modal batch melting, equation to use is: L C 1 = i O − + C ( F ( 1 D ) D ) i i i L C / L D First, we need to calculate for the crystalline assemblage using White’s D values i D Sr = (0.5x2.7) + (0.25x0.157) + (0.2x0.0068) + (0.05x.0099) = 1.39 D Rb = (0.5x0.025) + (0.25x0.033) + (0.2x0.022) + (0.05x0.007) = 0.025 L L L o C C Note: (1) dramatic C C 60 F L Rb Rb Rb Sr / decrease in Rb and L o o C C o C C Sr Sr 50 Rb/Sr as melting Rb Sr progresses. 0 .72 40.0 55.6 40 (2) Essentially 0.02 .723 22.5 31.1 0.05 .73 13.6 18.6 constant Sr during 30 L C Rb 0.1 .74 8.2 11.0 progressive melting. o C 0.2 .76 4.6 6.0 Rb 20 (3) Is it justified to L o C C 0.3 .79 3.1 4.0 Rb Rb / assume constant D 0.4 .81 2.4 3.0 L o C C 10 L C Sr Sr Sr values and modal This calculation assumes constant o C Sr melting? D values 0 0.1 0.3 0 0.2 0.4 F L