t
play

T Valve TC Plant TS TS - + Feedback Loop TC Steam - PowerPoint PPT Presentation

Nov 28, 2023 •129 likes •526 views

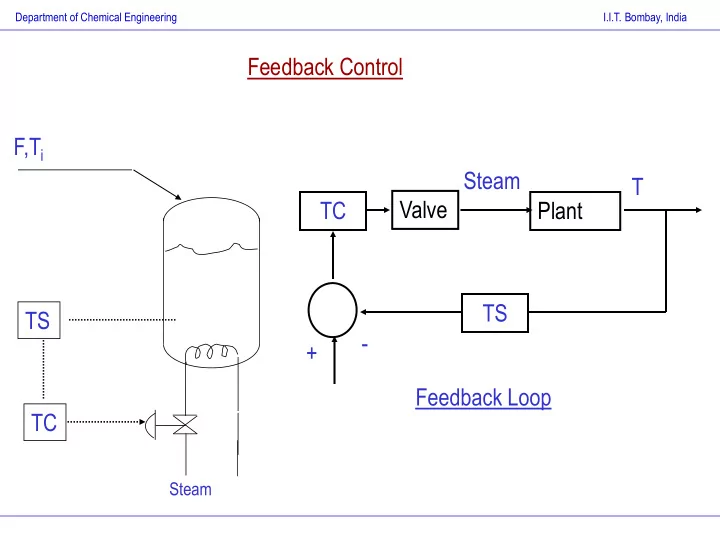
Department of Chemical Engineering I.I.T. Bombay, India Feedback Control F,T i Steam T Valve TC Plant TS TS - + Feedback Loop TC Steam Department of Chemical Engineering I.I.T. Bombay, India Typical Elements of the Feedback Loop

  1. Department of Chemical Engineering I.I.T. Bombay, India Feedback Control F,T i Steam T Valve TC Plant TS TS - + Feedback Loop TC Steam

  2. Department of Chemical Engineering I.I.T. Bombay, India Typical Elements of the Feedback Loop The plant Steam T Controller Signal Valve Plant (4-20 mA/ 1-5V/ 3-15 psi) Sensor T m , mV signal T TS Comparator + Setpoint Error signal, mV - T m

  3. Department of Chemical Engineering I.I.T. Bombay, India Typical Elements of the Feedback Loop Controller TC Error signal Signal to valve Valve / Actuator % valve opening / Controller output TS steam flowrate Typically valve and sensor dynamics are of simple first order type and are lumped into the plant dynamics.

  4. Department of Chemical Engineering I.I.T. Bombay, India Controller types for feedback control Proportional Controller c(t) = p(t) -p s = K c  (t) , where c is the controller output,  (t) is the error and p s is the output at zero error. In the laplace domain, c(s) = K c  (s) => g c (s) = c(s)/  (s) =K c K c is called the proportional gain of the controller and is sometimes represented as proportional band, PB. 100 .( maximum range of controller output) PB  K ( maximum range of measured variable) c

  5. Department of Chemical Engineering I.I.T. Bombay, India Controller types for feedback control Proportional + Integral Controller   t 1          c ( t ) p ( t ) p K ( t ) ( t ) dt  s c   I 0 where c is the controller output,  (t) is the error and p s is the output at zero error.    c ( s ) 1     g ( s ) K 1   c c   ( s ) s I The term  I is called the integral time, reset time and the reciprocal is called the reset time.

  6. Department of Chemical Engineering I.I.T. Bombay, India Integral action p t Integral action is usually used in conjunction with proportional mode. Interpreted as repetition of the proportional action after every integral time. With valve saturation, reset windup occurs

  7. Department of Chemical Engineering I.I.T. Bombay, India Controller types for feedback control Proportional + Integral + Derivative Controller    t 1 d ( t )            c ( t ) p ( t ) p K ( t ) ( t ) dt  s c D  dt  I 0 where c is the controller output,  (t) is the error and p s is the output at zero error.   c ( s ) 1        g ( s ) K 1 s   c c D   ( s ) s I The term  D is called the derivative time constant.

  8. Department of Chemical Engineering I.I.T. Bombay, India Closed Loop Transfer Functions Unlike in the open loop case, the closed loop has two independent inputs, viz. the set point and the disturbance. Assuming that all other elements such as valve and sensors are lumped with the process dynamics, the block diagram can be drawn as, d disturbance + + y d y Plant controller u + -

  9. Department of Chemical Engineering I.I.T. Bombay, India Closed Loop Transfer Functions From the previous block diagram, the following are true:   ( ) ( ) ( ) u s g s s c   y ( s ) g ( s ) u ( s ) g ( s ) d ( s ) p d    g ( s ) g ( s ) ( s ) g ( s ) d ( s ) p c d    ( ) ( ) ( ) s y s y s d Therefore,    y ( s ) g ( s ) g ( s ) y ( s ) g ( s ) g ( s ) y ( s ) g ( s ) d ( s ) p c p c d d g ( s ) g ( s ) g ( s )   p c d or , y ( s ) y ( s ) d ( s )   d 1 g ( s ) g ( s ) 1 g ( s ) g ( s ) p c p c Servo response Regulatory response

  10. Department of Chemical Engineering I.I.T. Bombay, India Closed loop response of first order + proportional (P) control K For g p (s)= and g c (s)=K c, the response to a unit step at the   s 1 set point is given by, KK c   1 KK 1 s 1   c y ( s )   KK s 1 KK   c 1 s 1 c    s 1 1 KK c The system responds like a first order process with a smaller time constant and a gain close to unity. The steady state error between the set point (unit step) and the process output y(t) is called the offset. Most processes under proportional control exhibit offset.

  11. Department of Chemical Engineering I.I.T. Bombay, India Closed loop response of first order + proportional (P) control Existence of off-set which decreases with increasing gain. Large gain can also result in instability and amplification of noise.

  12. Department of Chemical Engineering I.I.T. Bombay, India Closed loop response of first order + (PI) control   t 1  dy     and      u ( t ) K ( y y ) ( y y ) dt y Ku  c d d   dt I 0   t dy 1  Therefore,         y KK ( y y ) ( y y ) dt  c d d dt   I 0 2 d y dy KK      c ( 1 KK ) y y  1 c d 2 dt dt I Therefore the closed loop transfer function is second order with lead,   KK ( s 1 )  c I y ( s ) y ( s )       d 2 ( 1 ) s KK s KK 1 I I c c This could yield oscillatory response with possible overshoot. For a unit step change, it will reach set-point and exhibit zero offset. Integral action therefore increases the effective order of the system but gives zero offset.

  13. Department of Chemical Engineering I.I.T. Bombay, India Closed loop response of first order + (PI) control Integral action causes off-set to be zero High proportional gain causes oscillatory response High integral action leads to sluggish response

  14. Department of Chemical Engineering I.I.T. Bombay, India Closed loop response of first order + (PD) control     d dy    and    u ( t ) K y Ku   c  D  dt dt Therefore the closed loop transfer function is first order with lead term,   KK ( s 1 )  c D y ( s ) y ( s )      d ( ) 1 KK s KK c D c The overall order is therefore actually reduced. Transient response will be that of a lead lag system. It will exhibit steady state offset. Likewise for PID control, the closed loop transfer will have 2 poles and 2 zeros and due to integral mode, it will not exhibit offset.

  15. Department of Chemical Engineering I.I.T. Bombay, India Closed loop response of first order + (PID) control Derivative action leads to stability due the lead term in the transfer function.

  16. Department of Chemical Engineering I.I.T. Bombay, India Derivative mode illustration : on-off control of a heater.

  17. Department of Chemical Engineering I.I.T. Bombay, India Anticipatory action of the derivative mode Period Sign of Type of More or Corrective sign of Effect of error current less action de/dt derivative action necessary action (0,t 1 ) positive heating more decrease negative decrease heat heat (t 1 ,t 2 ) negative cooling less increase negative increase cooling cooling (t 2 ,t 3 ) negative cooling more decrease positive decrease cooling cooling

  18. Department of Chemical Engineering I.I.T. Bombay, India Integral action and offset removal Consider that at steady state, the steam flow rate is 100 kg/hr and the temperature is 200 o C. Suppose that a setpoint change to 205 o C is introduced. Let us now consider how a P and PI controller would behave at steady state in closed loop.  du ( t ) d ( t ) and therefore  c   The equation is K u ( t ) K ( t ) c dt dt  du ( t ) d ( t ) At steady state, rate of change is zero and therefore   0 dt dt This could happen only if  is a zero or a non-zero constant. If  is a zero, the deviation in steam flowrate u will be zero and also error between setpoint and CV is zero. This is not possible physically as you cannot get temperature to rise without supplying additional steam. Therefore,  = 0

  19. Department of Chemical Engineering I.I.T. Bombay, India Integral action and offset removal t K      c For PI control, the equation is u ( t ) K ( t ) ( t ) dt  c I 0  du ( t ) d ( t ) 1    and therefore K ( t )  c dt dt I  du ( t ) d ( t ) At steady state, rate of change is zero and therefore   0 dt dt This means that the error must go to zero at steady state and the extra control effort comes from the integral term. This ensures that a nonzero deviation in the control effort is available through integral action.

  20. Department of Chemical Engineering I.I.T. Bombay, India Anti-reset wind up schemes

  21. Department of Chemical Engineering I.I.T. Bombay, India Lectures 14 : Stability with Feedback and Controller Design

  22. Department of Chemical Engineering I.I.T. Bombay, India Closed Loop Stability   Characteristic Equation 1 g ( s ) g ( s ) 0 c p Analysis of the roots of this equation tells us about the stability of the closed loop system. But this is really a function of the controller parameters through the term g c (s) and therefore design methods need to include stability as a first criterion. The stable region is first determined before the controller design task is taken up.

Recommend

More recommend