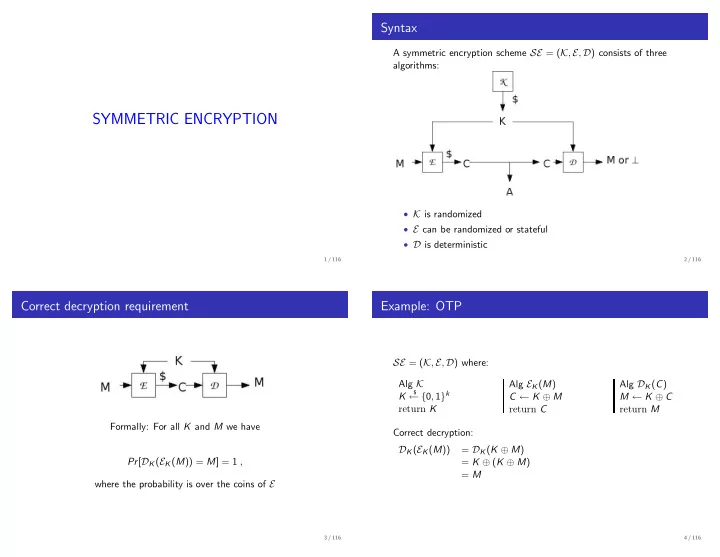

Syntax A symmetric encryption scheme SE = ( K , E , D ) consists of three algorithms: SYMMETRIC ENCRYPTION • K is randomized • E can be randomized or stateful • D is deterministic 1 / 116 2 / 116 Correct decryption requirement Example: OTP SE = ( K , E , D ) where: Alg K Alg E K ( M ) Alg D K ( C ) ← { 0 , 1 } k $ K C ← K ⊕ M M ← K ⊕ C return K return C return M Formally: For all K and M we have Correct decryption: D K ( E K ( M )) = D K ( K ⊕ M ) Pr [ D K ( E K ( M )) = M ] = 1 , = K ⊕ ( K ⊕ M ) = M where the probability is over the coins of E 3 / 116 4 / 116
Block cipher modes of operation Block cipher modes of operation Block cipher provides parties sharing K with E : { 0 , 1 } k × { 0 , 1 } n → { 0 , 1 } n a block cipher M Notation: x [ i ] is the i-th n-bit block of a string x, so that x = x [1] . . . x [ m ] if | x | = nm . Always: E K Alg K ← { 0 , 1 } k $ K C return K which enables them to encrypt a 1-block message. How do we encrypt a long message using a primitive that only applies to n-bit blocks? 5 / 116 6 / 116 ECB: Electronic Codebook Mode Evaluating Security SE = ( K , E , D ) where: Sender encrypts some messages M 1 , ..., M q , namely Alg E K ( M ) Alg D K ( C ) $ $ ← E K ( M 1 ) , ..., C q ← E K ( M q ) C 1 for i = 1 , . . . , m do for i = 1 , . . . , m do and transmits C 1 , ..., C q to receiver. M [ i ] ← E − 1 C [ i ] ← E K ( M [ i ]) K ( C [ i ]) return C return M Adversary • Knows SE = ( K , E , D ) • Knows C 1 , ..., C q • Is not given K ! Possible adversary goals: • Recover K • Recover M 1 Correct decryption relies on E being a block cipher, so that E K is But we will need to look beyond these invertible 7 / 116 8 / 116
Security of ECB Security of ECB Weakness: M 1 = M 2 ⇒ C 1 = C 2 Why is the above true? Because E K is deterministic: M 1 [1] M 1 [ m ] M 2 [1] M 2 [ m ] . . . . . . E K E K E K E K Adversary has ciphertext C = C [1] · · · C [ m ] C 1 [1] C 1 [ m ] C 2 [1] C 2 [ m ] Adversary task Assessment Why? Compute K seems hard E is secure Compute M [1] seems hard E is secure Why does this matter? 9 / 116 10 / 116 Security of ECB Security of ECB Suppose we know that there are only two possible messages, Y = 1 n Votes M 1 , M 2 ∈ { Y , N } are ECB encrypted and adversary sees and N = 0 n , for example representing ciphertexts C 1 = E K ( M 1 ) and C 2 = E K ( M 2 ) • FIRE or DON’T FIRE a missile M 1 M 2 • BUY or SELL a stock • Vote YES or NO Then ECB algorithm will be E K ( M ) = E K ( M ). E K E K M C 1 C 2 Adversary may have cast the first vote and thus knows M 1 ; say E K M 1 = Y . Then adversary can figure out M 2 : • If C 2 = C 1 then M 2 must be Y C • Else M 2 must be N 11 / 116 12 / 116
Is this avoidable? Randomized encryption Let SE = ( K , E , D ) be ANY encryption scheme. For encryption to be secure it must be randomized Suppose M 1 , M 2 ∈ { Y , N } and That is, algorithm E K flips coins. • Sender sends ciphertexts C 1 ← E K ( M 1 ) and C 2 ← E K ( M 2 ) If the same message is encrypted twice, we are likely to get back • Adversary A knows that M 1 = Y different answers. That is, if M 1 = M 2 and we let $ $ ← E K ( M 1 ) and C 2 ← E K ( M 2 ) C 1 Adversary says: If C 2 = C 1 then M 2 must be Y else it must be N. then Does this attack work? Pr [ C 1 = C 2 ] will (should) be small, where the probability is over the coins of E . Yes, if E is deterministic. 13 / 116 14 / 116 Randomized encryption Randomized encryption There are many possible ciphertexts corresponding to each message. If so, how can we decrypt? A fundamental departure from classical and conventional notions of We will see examples soon. encryption. Clasically, encryption (e.g., substitution cipher) is a code, associating to each message a unique ciphertext. C 1 Now, we are saying no such code is secure, and we look to encryption C 2 mechanisms which associate to each message a number of different E K D K M M possible ciphertexts. C s 15 / 116 16 / 116
Stateful encryption More Modes of Operation An alternative to randomization is to allow the encryption algorithm to maintain state. This might be a counter Randomized Stateful • encrypt depending on counter value • then update counter CBC$, CTR$ CBCC,CTRC We will see schemes that use this paradigm to get around the security weaknesses of deterministic encryption without using randomness. 17 / 116 18 / 116 CBC$: Cipher Block Chaining with random IV mode CTRC mode SE = ( K , E , D ) where: Sender maintains a counter ctr that is initially 0 and is updated by E � j � = the n -bit binary representation of integer j (0 ≤ j < 2 n ) Alg E K ( M ) Alg D K ( C ) Alg E K ( M ) $ ← { 0 , 1 } n C [0] Alg D K ( C ) for i = 1 , . . . , m do C [0] ← ctr for i = 1 , . . . , m do M [ i ] ← E − 1 ctr ← C [0] K ( C [ i ]) ⊕ C [ i − 1] for i = 1 , . . . , m do C [ i ] ← E K ( M [ i ] ⊕ C [ i − 1]) for i = 1 , . . . , m do return M P [ i ] ← E K ( � ctr + i � ) return C P [ i ] ← E K ( � ctr + i � ) C [ i ] ← P [ i ] ⊕ M [ i ] M [ i ] ← P [ i ] ⊕ C [ i ] ctr ← ctr + m return M return C Correct decryption relies on E being a block cipher so that E K is invertible 19 / 116 20 / 116 • Decryptor does not maintain a counter − 1 ! • D does not use
Security of CBC$ against key recovery Voting with CBC$ If adversary has a plaintext M and corresponding ciphertext Suppose we encrypt M 1 , M 2 ∈ { Y , N } with CBC$. $ C ← E K ( M ) then it has input-output examples M 1 M 2 ( M [1] ⊕ C [0] , C [1]) , ( M [2] ⊕ C [1] , C [2]) of E K . M [1] M [2] E K E K E K E K $ $ { 0 , 1 } n { 0 , 1 } n → C 1 [0] C 1 [1] → C 2 [0] C 2 [1] C [2] C [0] C [1] Adversary A sees C 1 = C 1 [0] C 1 [1] and C 2 = C 2 [0] C 2 [1]. So chosen-message key recovery attacks on E can be mounted to Suppose A knows that M 1 = Y . recover K . Can A determine whether M 2 = Y or M 2 = N ? Conclusion: Security of CBC$ against key recovery is no better than NO! that of the underlying block cipher. 21 / 116 22 / 116 Voting with CBC$ Assessing security If M 1 = Y we have C 1 [0] ⊕ Y C 2 [0] ⊕ M 2 So CBC$ is better than ECB. But is it secure? E K E K CBC$ is the world’s most widely used encryption scheme (SSL, SSH, TLS, ...) so knowing whether it is secure is important C 1 [1] C 2 [1] To answer this we first need to decide and formalize what we mean by secure. A knows C 1 [0] C 1 [1] and C 2 [0] C 2 [1]. Now • If C 1 [0] = C 2 [0] then A can deduce that • If C 2 [1] = C 1 [1] then M 2 = Y • If C 2 [1] � = C 1 [1] then M 2 = N • But the probability that C 1 [0] = C 2 [0] is very small. 23 / 116 24 / 116
Types of encryption schemes Security requirements Special purpose: Used in a specific setting, to encrypt data of some known format or distribution. Comes with a WARNING! only use under conditions X. A priori information: What the adversary already knows about the data from the context. For example, it is drawn from { Y , N } General purpose: Used to encrypt in many different settings, where the data format and distribution are not known in advance. Data distribution or format: The data may be English or not; may have randomness or not; ... We want general purpose schemes because • They can be standardized and broadly used. Security should not rely on assumptions about these things. • Once a scheme is out there, it gets used for everything anyway. • General purpose schemes are easier to use and less subject to mis-use: it is hard for application designers to know whether condition X is met. 25 / 116 26 / 116 E-mail encryption Security requirements Suppose sender computes E-mail data could be $ $ C 1 ← E K ( M 1 ) ; · · · ; C q ← E K ( M q ) • English text Adversary A has C 1 , . . . , C q • A pdf or executable file • Votes What if A Retrieves K Bad! Want security in all these cases. Retrieves M 1 Bad! But also ... 27 / 116 28 / 116
Security requirements What we seek We want a single “master” property MP of an encryption scheme such that • MP can be easily specified We want to hide all partial information about the data stream. • We can evaluate whether a scheme meets it Examples of partial information: • MP implies ALL the security conditions we want: it guarantees that • Does M 1 = M 2 ? a ciphertext reveals NO partial information about the plaintext. • What is first bit of M 1 ? Thus a scheme having MP means not only that if adversary has • What is XOR of first bits of M 1 , M 2 ? $ $ ← E K ( M 1 ) and C 2 ← E K ( M 2 ) then C 1 Something we won’t hide: the length of the message • It can’t get M 1 • It can’t get 1st bit of M 1 • It can’t get XOR 1st bits of M 1 , M 2 but in fact implies “all” such information about M 1 , M 2 is protected. 29 / 116 30 / 116 Seeking MP Plan • Define IND-CPA So what is the master property MP? • Examples of non-IND-CPA schemes It is a notion we call indistinguishability (IND). We will define • See why IND-CPA is a “master” property, namely why it implies • IND-CPA: Indistinguishability under chosen-plaintext attack that ciphertexts leak no partial information about plaintexts • Examples of IND-CPA schemes • IND-CCA: Indistinguishability under chosen-ciphertext attack • IND-CCA 31 / 116 32 / 116
Recommend
More recommend