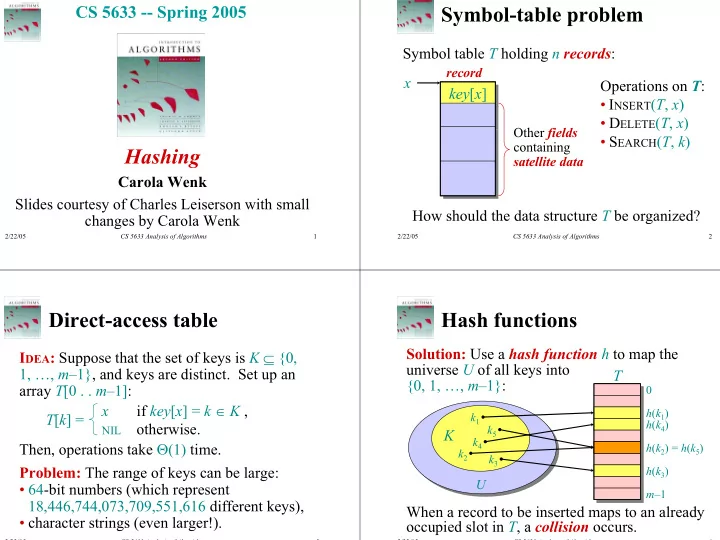

CS 5633 -- Spring 2005 Symbol-table problem Symbol table T holding n records : record x Operations on T : key [ x ] key [ x ] • I NSERT ( T , x ) • D ELETE ( T , x ) Other fields • S EARCH ( T , k ) containing Hashing satellite data Carola Wenk Slides courtesy of Charles Leiserson with small How should the data structure T be organized? changes by Carola Wenk 2/22/05 CS 5633 Analysis of Algorithms 1 2/22/05 CS 5633 Analysis of Algorithms 2 Direct-access table Hash functions Solution: Use a hash function h to map the I DEA : Suppose that the set of keys is K ⊆ {0, universe U of all keys into 1, …, m –1}, and keys are distinct. Set up an T {0, 1, …, m –1}: array T [0 . . m –1]: 0 if key [ x ] = k ∈ K , x h ( k 1 ) k 1 T [ k ] = h ( k 4 ) otherwise. NIL k 5 K k 4 Then, operations take Θ (1) time. h ( k 2 ) = h ( k 5 ) k 2 k 3 Problem: The range of keys can be large: h ( k 3 ) U • 64-bit numbers (which represent m –1 18,446,744,073,709,551,616 different keys), When a record to be inserted maps to an already As each key is inserted, h maps it to a slot of T . • character strings (even larger!). occupied slot in T , a collision occurs. 2/22/05 CS 5633 Analysis of Algorithms 3 2/22/05 CS 5633 Analysis of Algorithms 4
Resolving collisions by Analysis of chaining chaining We make the assumption of simple uniform • Records in the same slot are linked into a list. hashing: • Each key k ∈ K of keys is equally likely to T be hashed to any slot of table T , independent of where other keys are hashed. Let n be the number of keys in the table, and 49 86 52 let m be the number of slots. i 49 86 52 Define the load factor of T to be h (49) = h (86) = h (52) = i α = n / m = average number of keys per slot. 2/22/05 CS 5633 Analysis of Algorithms 5 2/22/05 CS 5633 Analysis of Algorithms 6 Search cost Choosing a hash function The assumption of simple uniform hashing Expected time to search for a record with is hard to guarantee, but several common a given key = Θ (1 + α ). techniques tend to work well in practice as long as their deficiencies can be avoided. apply hash search function and the list Desirata: access slot • A good hash function should distribute the Expected search time = Θ (1) if α = O (1), keys uniformly into the slots of the table. or equivalently, if n = O ( m ). • Regularity in the key distribution should not affect this uniformity. 2/22/05 CS 5633 Analysis of Algorithms 7 2/22/05 CS 5633 Analysis of Algorithms 8
Division method Division method (continued) Assume all keys are integers, and define h ( k ) = k mod m. h ( k ) = k mod m. Pick m to be a prime not too close to a power Deficiency: Don’t pick an m that has a small of 2 or 10 and not otherwise used prominently divisor d . A preponderance of keys that are in the computing environment. congruent modulo d can adversely affect uniformity. Annoyance: • Sometimes, making the table size a prime is Extreme deficiency: If m = 2 r , then the hash inconvenient. doesn’t even depend on all the bits of k : • If k = 1011000111011010 2 and r = 6, then h ( k ) = 011010 2 . h ( k ) 2/22/05 CS 5633 Analysis of Algorithms 9 2/22/05 CS 5633 Analysis of Algorithms 10 Resolving collisions by open Example of open addressing addressing No storage is used outside of the hash table itself. Insert key k = 496: T • Insertion systematically probes the table until an 0 empty slot is found. 0. Probe h (496,0) 586 • The hash function depends on both the key and 133 probe number: collision 204 204 h : U × {0, 1, …, m –1} → {0, 1, …, m –1}. • The probe sequence 〈 h ( k ,0), h ( k ,1), …, h ( k , m –1) 〉 481 should be a permutation of {0, 1, …, m –1}. m –1 • The table may fill up, and deletion is difficult (but not impossible). 2/22/05 CS 5633 Analysis of Algorithms 11 2/22/05 CS 5633 Analysis of Algorithms 12
Example of open addressing Example of open addressing Insert key k = 496: Insert key k = 496: T T 0 0 0. Probe h (496,0) 0. Probe h (496,0) collision 586 586 586 1. Probe h (496,1) 1. Probe h (496,1) 133 133 2. Probe h (496,2) 204 204 insertion 496 481 481 m –1 m –1 2/22/05 CS 5633 Analysis of Algorithms 13 2/22/05 CS 5633 Analysis of Algorithms 14 Example of open addressing Probing strategies Linear probing: Search for key k = 496: T Given an ordinary hash function h ′ ( k ), linear 0 0. Probe h (496,0) probing uses the hash function 586 1. Probe h (496,1) h ( k , i ) = ( h ′ ( k ) + i ) mod m . 133 2. Probe h (496,2) This method, though simple, suffers from primary 204 496 clustering , where long runs of occupied slots build Search uses the same probe 481 up, increasing the average search time. Moreover, sequence, terminating suc- m –1 the long runs of occupied slots tend to get longer. cessfully if it finds the key and unsuccessfully if it encounters an empty slot. 2/22/05 CS 5633 Analysis of Algorithms 15 2/22/05 CS 5633 Analysis of Algorithms 16
Probing strategies Analysis of open addressing Double hashing We make the assumption of uniform hashing: Given two ordinary hash functions h 1 ( k ) and h 2 ( k ), • Each key is equally likely to have any one of double hashing uses the hash function the m ! permutations as its probe sequence. h ( k , i ) = ( h 1 ( k ) + i ⋅ h 2 ( k )) mod m . Theorem. Given an open-addressed hash This method generally produces excellent results, table with load factor α = n / m < 1, the but h 2 ( k ) must be relatively prime to m . One way expected number of probes in an unsuccessful is to make m a power of 2 and design h 2 ( k ) to search is at most 1/(1– α ). produce only odd numbers. 2/22/05 CS 5633 Analysis of Algorithms 17 2/22/05 CS 5633 Analysis of Algorithms 18 Proof of the theorem Proof (continued) Proof. Therefore, the expected number of probes is • At least one probe is always necessary. − − n n 1 n 2 1 + + + + 1 1 1 1 L L • With probability n / m , the first probe hits an − − − + m m 1 m 2 m n 1 occupied slot, and a second probe is necessary. ( ( ( ( ) ) ) ) ≤ + α + α + α + α 1 1 1 1 L L • With probability ( n –1)/( m –1), the second probe hits an occupied slot, and a third probe is 2 3 ≤ + α + α + α + 1 L necessary. ∞ ∑ • With probability ( n –2)/( m –2), the third probe i = α The textbook has a hits an occupied slot, etc. = i 0 more rigorous proof. − n i n 1 < = α Observe that for i = 1, 2, …, n . . = − m i m − α 1 2/22/05 CS 5633 Analysis of Algorithms 19 2/22/05 CS 5633 Analysis of Algorithms 20
Implications of the theorem • If α is constant, then accessing an open- addressed hash table takes constant time. • If the table is half full, then the expected number of probes is 1/(1–0.5) = 2. • If the table is 90% full, then the expected number of probes is 1/(1–0.9) = 10. 2/22/05 CS 5633 Analysis of Algorithms 21
Recommend
More recommend