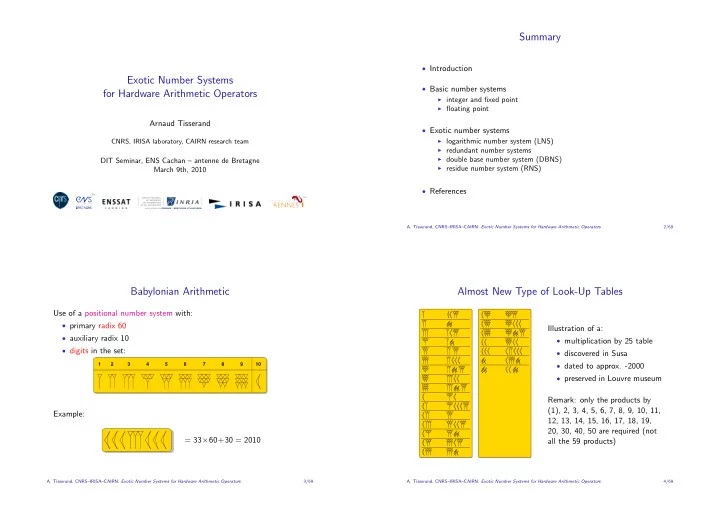

Summary • Introduction Exotic Number Systems • Basic number systems for Hardware Arithmetic Operators ◮ integer and fixed point ◮ floating point Arnaud Tisserand • Exotic number systems ◮ logarithmic number system (LNS) CNRS, IRISA laboratory, CAIRN research team ◮ redundant number systems ◮ double base number system (DBNS) DIT Seminar, ENS Cachan – antenne de Bretagne ◮ residue number system (RNS) March 9th, 2010 • References A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 2/69 Babylonian Arithmetic Almost New Type of Look-Up Tables Use of a positional number system with: • primary radix 60 Illustration of a: • auxiliary radix 10 • multiplication by 25 table • digits in the set: • discovered in Susa 1 2 3 4 5 6 7 8 9 10 • dated to approx. -2000 • preserved in Louvre museum Remark: only the products by (1), 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, Example: 12, 13, 14, 15, 16, 17, 18, 19, 20, 30, 40, 50 are required (not = 33 × 60+30 = 2010 all the 59 products) A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 3/69 A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 4/69
Egyptian Multiplication First Computer with a Floating-Point Unit Z3 designed by Konrad Zuse (1910–1995) in 1941, Berlin M ( n , m , p ) = n × m + p Rewriting rules: M (0 , m , p ) = ⇒ p M (2 n , m , p ) = ⇒ M ( n , 2 m , p ) M (2 n + 1 , m , p ) = ⇒ M ( n , 2 m , p + m ) Example: 12 × 12 = M (12 , 12 , 0) = M (6 , 24 , 0) = M (3 , 48 , 0) = M (1 , 96 , 48) picture of the version rebuilt in 1961 = M (0 , 192 , 144) Source: http://www.epemag.com/zuse/ = 144 A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 5/69 A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 6/69 Z3: Architecture and Characteristics Z3 : Data Format and Floating-Point Unit Floating-point representation: Memory Punched address (lamps) (keyboard) Tape • 1-bit sign 8 Output Input Reader • 7-bit exponent represented using 2’s complement data ◮ exponent = − 64 − 22 Control → 0 Unit ◮ exponent = 63 − → ∞ 5.33 Hertz instr. • 14-bit mantissa + 1 implicit bit data Clock generator Floating−point 22 Unit Floating-point unit: 22 • addition/subtraction 3 cycles (0.6 s/op.) reg 1 reg 2 • multiplication 16 cycles (3.0 s/op.) • division 18 cycles (3.4 s/op.) size 5 m × 2 m × 0.8 m • square root (variable latency) weight ≈ 1000 kg frequency 5.33 Hz technology elect. relays (num.: 600, mem.: 1400) Other instructions: read keyboard, display, load, store... power consumption ≈ 4000 W A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 7/69 A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 8/69
Intel 486 Processor Intel Xeon Core i7 (code name: Bloomfield) • 64-bit processor • 32-bit processor • quad core with 2 threads • embedded arithmetic co-processor • hyper-threading comm. 6.4 GT/s • first commercialization in 1989 • 3 DDR3-1066 links → 25.6 GB/s • frequencies: 50, 33 and 25,MHz • first commercialization in Q4.2008 • transistors number: 1 . 2 × 10 6 • frequencies: 2.66 to 3.33 GHz • technology: CMOS 0.8 or 1.0 µ m • transistors number: 731 × 10 6 • silicon area: 81 mm 2 • technology: CMOS 45 nm • power supply: 5 V • silicon area: 263 mm 2 • package: 168 PGA • power supply: 130 W under 1.375 V • pipeline: 5 stages • socket/package: 1366 LGA • L1 cache: 8 KB (4w SA, WT) • caches: 32 kB I + 32 kB D L1, • 1 ALU 4 × 256 kB L2, 8 MB L3 A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 9/69 A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 10/69 Research in Computer Arithmetic Design of Computer Arithmetic Operators implementations number systems x computer software: integer, redundant, func., lib(m) fixed/floating-point, arithmetic hardware: multiple precision, FPGA, ASIC RNS, LNS, DBNS. . . operator area, delay F p , F 2 m , F 3 m energy number t algorithms implement. arithmetic systems f ( x ) operations algorithms ± , × , ÷ , √ . . . target polynomial approx., cost op. mod, filters, function iterations, speed sin, cos, exp, log. . . tables and operations application area validation DCT, FFT, crypto.. . . digit recurrence. . . good adequacy memory test combinations constraints accuracy energy A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 11/69 A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 12/69
Some Problems in Computer Arithmetic Number Systems • better arithmetic primitives: • set of represented numbers ◮ speed (throughput, latency) ◮ integers: N , Z ◮ silicon area, program size, memory, # intermediate registers ◮ rationals: Q ◮ power consumption, energy per operation ◮ real approximations: subset of R ◮ complex approximations: subset of C ◮ finite fields: F p , F 2 m , F 3 m • limited support in design tools ◮ . . . software: integer, floating-point, libraries for many types • system properties hardware: integer, fixed-point, a few IP blocs ◮ positional or non positional ◮ redundant or non redundant • validation ◮ fixed precision or arbitrary precision (multiple precision) ◮ completeness (in a finite set) accuracy: error bounds, minimal precision, formal proof ◮ . . . behavior: overflows, Not a Number design: (formal) verification of the correctness of a program Number system = (function, library, hardware bloc, circuit) 1. data format and encoding run time: verification of the correctness of an implementation = 2. a set of interpretation rules for the encoding functional test A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 13/69 A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 14/69 Positional Number System(s) Radix-2 Signed Integers n − 1 � • sign and magnitude (absolute value) x i β i = ( x n − 1 x n − 2 · · · x 1 x 0 . x − 1 x − 2 · · · x − m ) X = i = − m n − 2 � A = ( s a a n − 2 . . . a 1 a 0 ) = ( − 1) s a × a i 2 i • radix β (usually a power of 2) i =0 • digits x i ( ∈ N ) in the digit set D • 2’s complement • rank or position i , weight β i • n integer digits, m fractional digits n − 2 � A = ( a n − 1 a n − 2 . . . a 1 a 0 ) = − a n − 1 2 n − 1 + a i 2 i Examples: i =0 • β = 10 , D = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 } • biased (usually B = 2 n − 1 − 1) • β = 2 , D = { 0 , 1 } • carry save: β = 2 , D cs = { 0 , 1 , 2 } A = A math + B • borrow save: β = 2 , D bs = {− 1 , 0 , 1 } • signed digits: β > 2 , D sd ,α,β = {− α, . . . , α } with 2 α + 1 ≥ β • . . . √ • theoretical systems: β = 1+ 5 , β = 1 + i . . . 2 A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 15/69 A. Tisserand, CNRS–IRISA–CAIRN. Exotic Number Systems for Hardware Arithmetic Operators 16/69
Recommend
More recommend