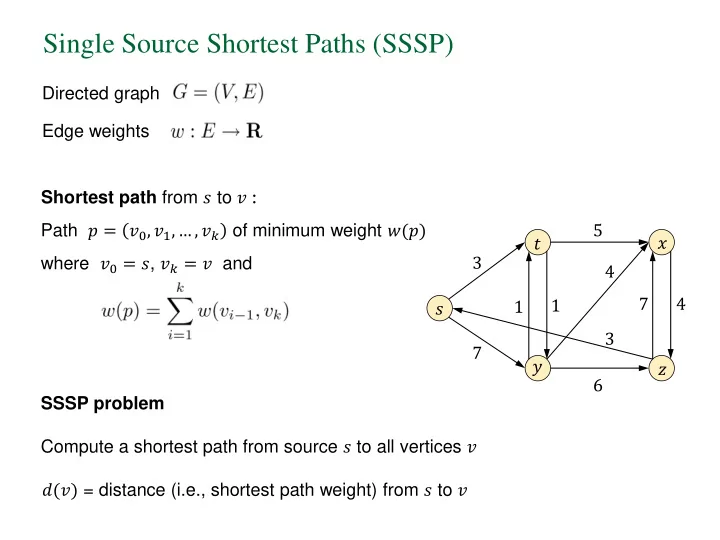
Single Source Shortest Paths (SSSP) Directed graph Edge weights - PowerPoint PPT Presentation

Single Source Shortest Paths (SSSP) Directed graph Edge weights Shortest path from 𝑡 to 𝑤 : Path 𝑞 = 𝑤 0 , 𝑤 1 , … , 𝑤 𝑙 of minimum weight 𝑥(𝑞) 5 𝑦 𝑢 3 where 𝑤 0 = 𝑡 , 𝑤 𝑙 = 𝑤 and 4 7 4 1 1 𝑡 3 7 𝑧 𝑨 6 SSSP problem Compute a shortest path from source 𝑡 to all vertices 𝑤 𝑒(𝑤) = distance (i.e., shortest path weight) from 𝑡 to 𝑤

Single Source Shortest Paths (SSSP) Directed graph Edge weights Shortest path from 𝑡 to 𝑤 : 𝑒(𝑦) = 8 𝑒(𝑢) = 3 Path 𝑞 = 𝑤 0 , 𝑤 1 , … , 𝑤 𝑙 of minimum weight 𝑥(𝑞) 5 𝑦 𝑢 3 where 𝑤 0 = 𝑡 , 𝑤 𝑙 = 𝑤 and 4 7 4 1 1 𝑡 3 7 𝑧 𝑨 6 𝑒(𝑧) = 4 𝑒(𝑧) = 10 SSSP problem Compute a shortest path from source 𝑡 to all vertices 𝑤 𝑒(𝑤) = distance (i.e., shortest path weight) from 𝑡 to 𝑤

Single Source Shortest Paths (SSSP) Parent of a vertex 𝑞 𝑤 = vertex just before 𝑤 on the shortest path from 𝑡 𝑞(𝑤) 𝑤 𝑡 Shortest paths tree 5 Formed by the edges (𝑞(𝑤), 𝑤) 𝑦 𝑢 3 4 𝑞(𝑡) = - 7 4 1 1 𝑡 𝑞(𝑢) = 𝑡 𝑞(𝑧) = 𝑢 3 7 𝑧 𝑨 𝑞(𝑦) = 𝑢 𝑞(𝑨) = 𝑧 6

Single Source Shortest Paths (SSSP) Temporary distances 𝑒(𝑤) = upper bound for the weight of the shortest path from 𝑡 to 𝑤 𝑞(𝑤) ← null , 𝑒(𝑤) ← ∞ for all 𝑤 ≠ 𝑡 Initialize 𝑞(𝑡) ← null , 𝑒(𝑡) ← 0 Edge relaxation relax (𝑣, 𝑤) 2 2 if if 𝑒(𝑤) > 𝑒(𝑣) + 𝑥(𝑣, 𝑤) 𝑣 𝑤 𝑣 𝑤 then { th 𝑒(𝑤) = 8 𝑒(𝑤) = 6 𝑒(𝑣) = 5 𝑒(𝑣) = 5 𝑒(𝑤) ← 𝑒(𝑣) + 𝑥(𝑣, 𝑤) 𝑞(𝑤) ← 𝑣 } 2 2 𝑤 𝑤 𝑣 𝑣 𝒆(𝒘) = 𝟖 𝑒(𝑤) = 6 𝑒(𝑣) = 5 𝑒(𝑣) = 5

Single Source Shortest Paths (SSSP) Dijkstra’s Algorithm Used when edge weights are non-negative It maintains a set of vertices 𝑇 ⊆ 𝑊 for which a shortest path has been computed, i.e., the value of 𝑒(𝑤) is the exact weight of the shortest path to 𝑤 . Each iteration selects a vertex 𝑣 ∈ 𝑊\S with minimum distance 𝑒(𝑣) . Then we set S ← 𝑇 ∪ 𝑣 and relax all edges (𝑣, 𝑥) To find 𝑣 with min 𝑒(𝑣) : Use a priority queue 𝑅 with keys

Single Source Shortest Paths (SSSP) Dijkstra’s Algorithm Initialization 𝑞(𝑤) ← null , 𝑒(𝑤) ← ∞ for all 𝑤 ≠ 𝑡 𝑞(𝑡) ← null , 𝑒(𝑡) ← 0 set 𝑇 ← ∅ insert all vertices 𝑤 into priority queue 𝑅 with key 𝑒(𝑤) Main Loop while 𝑅 is not empty { 𝑣 ← Q. delMin() 𝑇 ← 𝑇 ∪ 𝑣 for all edges (𝑣, 𝑤) { relax(𝑣, 𝑤) } }

Single Source Shortest Paths (SSSP) Dijkstra’s Algorithm Initialization 𝑞(𝑤) ← null , 𝑒(𝑤) ← ∞ for all 𝑤 ≠ 𝑡 𝑞(𝑡) ← null , 𝑒(𝑡) ← 0 set 𝑇 ← ∅ insert all vertices 𝑤 into priority queue 𝑅 with key 𝑒(𝑤) Main Loop priority queue 𝑅 running time while 𝑅 is not empty { O(𝑜 2 ) array 𝑣 ← Q. delMin() 𝑇 ← 𝑇 ∪ 𝑣 O(𝑛 log 𝑜) binary heap for all edges (𝑣, 𝑤) { O(𝑛 + 𝑜 log 𝑜) Fibonacci heap relax(𝑣, 𝑤) } }

Single Source Shortest Paths (SSSP) in Map-Reduce ➢ Not easy to parallelize Dijkstra’s algorithm ➢ Use an iterative approach instead • The distance 𝑒(𝑤) from 𝑡 to 𝑤 is updated by the distances of all 𝑣 with 𝑣, 𝑤 ∈ 𝐹 . 𝑦 𝑧 𝑥(𝑦, 𝑤) 𝑥(𝑧, 𝑤) 𝑒(𝑤) ← min 𝑒 𝑣 + 𝑥 𝑣, 𝑤 | (𝑣, 𝑤) ∈ 𝐹 𝑤 𝑨 𝑥(𝑨, 𝑤) • Need to communicate both distances and adjacency lists.

Single Source Shortest Paths (SSSP) in Map-Reduce Mapper: emits distances and graph structure 𝑒 𝑤 + 𝑥(𝑤, 𝑏) 𝑏 𝑤 𝑐 𝑒 𝑤 + 𝑥(𝑤, 𝑐) 𝑑 𝑒 𝑤 + 𝑥(𝑤, 𝑑) Reducer: updates distances and emits graph structure 𝑦 𝑧 𝑥(𝑦, 𝑤) 𝑥(𝑧, 𝑤) 𝑒(𝑤) ← min 𝑒 𝑣 + 𝑥 𝑣, 𝑤 | (𝑣, 𝑤) ∈ 𝐹 𝑤 𝑨 𝑥(𝑨, 𝑤)

Single Source Shortest Paths (SSSP) in Map-Reduce ➢ Not easy to parallelize Dijkstra’s algorithm ➢ Use an iterative approach instead • The distance 𝑒(𝑤) from 𝑡 to 𝑤 is updated by the distances of all 𝑣 with 𝑣, 𝑤 ∈ 𝐹 . • Need to communicate both distances and adjacency lists. • Repeat round until all distances are fixed. • Number of rounds = 𝑜 − 1 in the worst case. • If all weights are equal then we compute the Breadth-First Search (BFS) tree. Number of rounds = graph diameter.

BFS in Map-Reduce

Single Source Shortest Paths (SSSP) in Map-Reduce Remarks on Map-Reduce SSSP algorithm • Essentially a brute -force algorithm. • Performs many unnecessary computations. • No global data structure.

PageRank in Map-Reduce Recall the formula for the PageRank 𝑆(𝑣) of a webpage 𝑣 𝑆(𝑤) 𝑆 𝑣 = 𝑑 ෍ + (1 − 𝑑)𝐹 𝑣 𝑂 𝑤 𝑤∈𝐶 𝑣 𝐶 𝑣 = set of pages that point to 𝑣 𝐺 𝑣 = set of pages that 𝑣 points to 𝐺 𝑣 = 𝑂 𝑣 = number of links from 𝑣 𝐹 𝑣 = probabilities over web pages 𝐹 𝑣 and 𝑑 are user designed parameters

PageRank in Map-Reduce Iterative computation start with seed values 𝑆 0 (𝑤) for each page 𝑤 each page 𝑤 receives credit each page 𝑤 distributes credit from the pages in 𝐶 𝑤 to the pages in 𝐺 𝑤 and computes 𝑆 𝑗+1 (𝑤)

PageRank in Map-Reduce

Algorithms and Complexity in MapReduce (and related models) Sorting, Searching, and Simulation in the MapReduce Framework M. T. Goodrich, N. Sitchinava, and Q. Zhang ISAAC 2011 Fast Greedy Algorithms in MapReduce and Streaming R. Kumar, B. Moseley, S. Vassilvitskii, and A. Vattani SPAA 2013 On the Computational Complexity of MapReduce B. Fish, J. Kun, A. D. Lelkes, L. Reyzin, and G. Turan DISC 2015

BSP model L. G. Valiant, A Bridging Model for Parallel Computation, Communications of the ACM, 1990 Computational model of parallel computation BSP is a parallel programming model based on Synchronizer Automata. The model consists of: • Set of processor-memory pairs. • Communications network that delivers messages in a point-to-point manner. • Mechanism for the efficient barrier synchronization for all or a subset of the processes. • No special combining, replicating, or broadcasting facilities.

BSP model • Vertical Structure Virtual Processors Supersteps: Local – Local computation Computation – Process Communication – Barrier Synchronization • Horizontal Structure – Concurrency among a fixed Global number of virtual processors. Communication – Processes do not have a particular order. – Locality plays no role in the placement of processes on Barrier Synchronization processors. Implementation: BSPlib

MapReduce simulation of a BSP program Simulation on MapReduce: 1. Create a tuple for each memory cell and processor. 2. Map each message to the destination processor label. 3. Reduce by performing one step of a processor, outputting the messages for next round. Theorem [Goodrich et al.]: Given a BSP algorithm 𝐵 that runs in 𝑈 supersteps with a total memory size 𝑂 using 𝑄 ≤ 𝑂 processors, we can simulate 𝐵 using O(𝑈) rounds and message complexity O(𝑈𝑂) in the memory-bound MapReduce framework with reducer memory size bounded by 𝑂/𝑄 .

MapReduce simulation of a BSP program Simulation on MapReduce: 1. Create a tuple for each memory cell and processor. 2. Map each message to the destination processor label. 3. Reduce by performing one step of a processor, outputting the messages for next round. Theorem [Goodrich et al.]: Given a BSP algorithm 𝐵 that runs in 𝑈 supersteps with a total memory size 𝑂 using 𝑄 ≤ 𝑂 processors, we can simulate 𝐵 using O(𝑈) rounds and message complexity O(𝑈𝑂) in the memory-bound MapReduce framework with reducer memory size bounded by 𝑂/𝑄 . A corollary of the above: Given the optimal BSP algorithm of [Goodrich, 99], we can sort 𝑂 values in the MapReduce framework in 𝑃(𝑙) rounds and 𝑃(𝑙𝑂) message complexity.

Algorithms and Complexity in MapReduce (and related models) Theorem [Fish et al.] : Any problem requiring sublogarithmic space, 𝑝(log 𝑜 ) , can be solved in MapReduce in two rounds. The proof is constructive : Given a problem that classically takes less than logarithmic space, there is an automatic algorithm to implement it in MapReduce