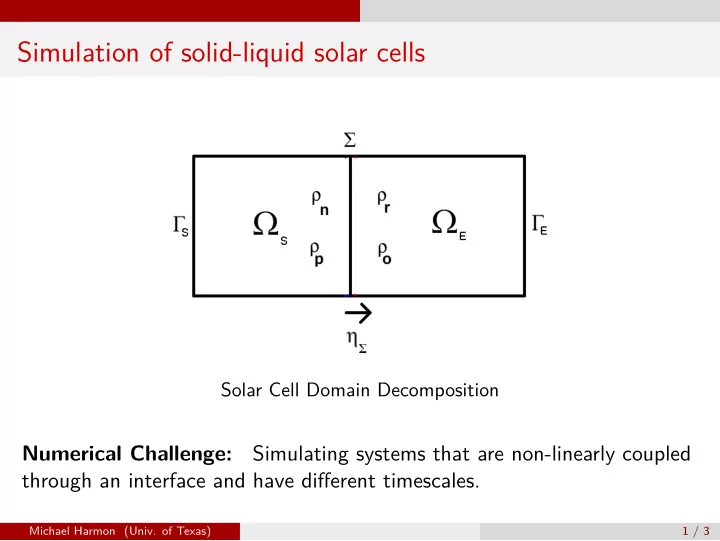
Simulation of solid-liquid solar cells Solar Cell Domain - PowerPoint PPT Presentation

Simulation of solid-liquid solar cells Solar Cell Domain Decomposition Simulating systems that are non-linearly coupled Numerical Challenge: through an interface and have different timescales. Michael Harmon (Univ. of Texas) 1 / 3

Flow-transport with a non-linear reactive interface Transport in subdomains: � ∂ t ρ n + J n ∇ · ( ∇ Φ ρ n − ∇ ρ n ) = − R ( ρ n , ρ p ) + G ( x ) Ω S ∂ t ρ p + J p ∇ · ( − ∇ Φ ρ p − ∇ ρ p ) = − R ( ρ n , ρ p ) + G ( x ) � ∂ t ρ r + J r ∇ · ( ∇ Φ ρ r − ∇ ρ r ) = 0 Ω E ∂ t ρ o + J o ∇ · ( − ∇ Φ ρ o − ∇ ρ p ) = 0  J n ( ∇ Φ ρ n − ∇ ρ n ) · η = k et ( ρ n − ρ e n ) ρ o   J p ( ∇ Φ ρ p − ∇ ρ p ) · η = k ht ( ρ p − ρ e  p ) ρ r  Σ J r ( ∇ Φ ρ r − ∇ ρ r ) · η = k ht ( ρ p − ρ e p ) ρ r − k et ( ρ n − ρ e n ) ρ o    J o ( ∇ Φ ρ o − ∇ ρ o ) · η = − k ht ( ρ p − ρ e p ) ρ r + k et ( ρ n − ρ e  n ) ρ o Flow in entire domain: � C ( x ) − ( ρ n − ρ p ) in Ω S − ∇ · ( λ ( x ) ∇ Φ) = − ( ρ r − ρ o ) in Ω E Michael Harmon (Univ. of Texas) 2 / 3

Numerical methods and problems Have : Flow-transport code that uses a mixed finite element method (MFEM) for flow equation and local discontinuous Galerkin (LDG) method for transport equations. Have: Code that solves diffusion equations which are non-linearly coupled through interface using LDG in space and time lagging (forward Euler) for linearization. Problem: Slow convergence to steady state solutions because linearization imposes severe constraint on time step. Need: Use big time steps. Need: Non-linear solver which is fast and easy to implement in deal.ii. (Newton-type method?) Need: Advice on best way to set up data structures. Michael Harmon (Univ. of Texas) 3 / 3