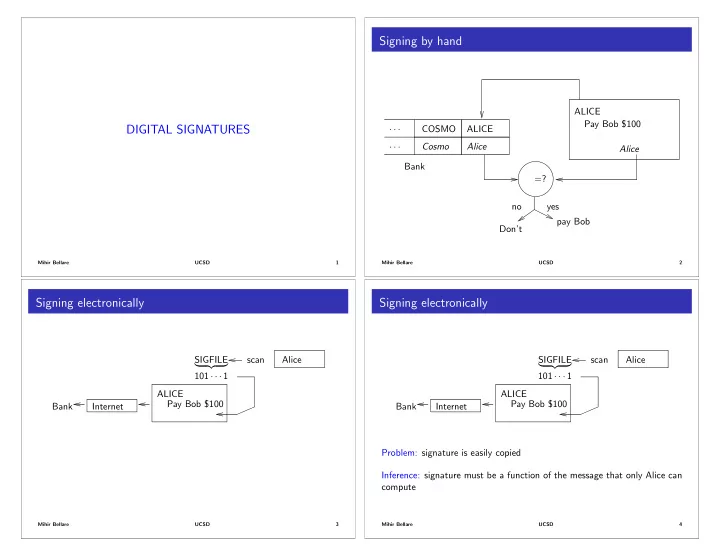

Signing by hand ALICE Pay Bob $100 DIGITAL SIGNATURES · · · COSMO ALICE · · · Cosmo Alice Alice Bank =? no yes pay Bob Don’t Mihir Bellare UCSD 1 Mihir Bellare UCSD 2 Signing electronically Signing electronically SIGFILE scan Alice SIGFILE scan Alice | {z } | {z } 101 · · · 1 101 · · · 1 ALICE ALICE Pay Bob $100 Pay Bob $100 Bank Internet Bank Internet Problem: signature is easily copied Inference: signature must be a function of the message that only Alice can compute Mihir Bellare UCSD 3 Mihir Bellare UCSD 4
What about a MAC? Digital signatures A digital signature scheme DS = ( K , S , V ) is a triple of algorithms where Let Bank and Alice share a key K K pk Internet ALICE MAC K Pay Bob $100 Bank sk T V σ 0 S σ A M M 0 A digital signature will have additional attributes: • Even the bank cannot forge 0/1 • Verifier does not need to share a key with signer or, indeed, have any secrets Correctness: V ( pk , M , S ( sk , M )) = 1 with probability one for all M . Mihir Bellare UCSD 5 Mihir Bellare UCSD 6 Usage Step 2: Dissemination of public keys Step 1: key generation $ Alice lets ( pk , sk ) K and stores sk (securely). The public key does not have to be kept secret but a verifier needs to know it is authentic, meaning really Alice’s public key and not someone else’s. Step 2: pk dissemination Alice enables any potential verifier to get pk . Alice could put her public key pk on her webpage, her Facebook, a key server or include it as an email attachment. Step 3: sign Alice can generate a signature σ of a document M using sk . Common method of dissemination is via certificates as discussed later. Step 4: verify Anyone holding pk can verify that σ is Alice’s signature on M . Mihir Bellare UCSD 7 Mihir Bellare UCSD 8
UF-CMA Security of a DS scheme UF-CMA Security of a DS scheme Let DS = ( K , S , V ) be a signature scheme and A an adversary. Game UF-CMA DS Intent: adversary cannot get a verifier to accept σ as Alice’s signature of procedure Initialize M unless Alice has really previously signed M , even if adversary can obtain procedure Sign ( M ) $ ( pk , sk ) K ; S ; Alice’s signatures on messages of the adversary’s choice. $ S ( sk , M ) σ return pk S S [ { M } procedure Finalize ( M , σ ) return σ As with MA schemes, the definition does not require security against d V ( pk , M , σ ) replay. That is handled on top, via counters or time stamps. return ( d = 1 ^ M / 2 S ) The uf-cma advantage of A is Adv uf - cma ⇥ ⇤ UF-CMA A ( A ) = Pr DS ) true DS Mihir Bellare UCSD 9 Mihir Bellare UCSD 10 UF-CMA: Explanations RSA signatures The “return pk ” statement in Initialize means the adversary A gets the public key pk as input. It does not get sk . Fix an RSA generator K rsa and let the key generation algorithm be It can call Sign with any message M of its choice to get back a correct $ signature σ S ( sk , M ) of M under sk . Notation indicates signing Alg K algorithm may be randomized. $ ( N , p , q , e , d ) K rsa To win, it must output a message M and a signature σ that are pk ( N , e ); sk ( N , d ) • Correct: V ( pk , M , σ ) = 1 Return ( pk , sk ) • New: M 62 S , meaning M was not a query to Sign We will use these keys in all our RSA-based schemes and only describe signing and verifying. Interpretation: Sign represents the signer and Finalize represents the verifier. Security means that the adversary can’t get the verifier to accept a message that is not authentic, meaning was not already signed by the sender. Mihir Bellare UCSD 11 Mihir Bellare UCSD 12
Plain RSA signature scheme Security of plain RSA signatures To forge signature of a message y , the adversary, given N , e but not d , Signer pk = ( N , e ) and sk = ( N , d ) must compute y d mod N , meaning invert the RSA function f at y . Alg S N , d ( y ) Alg V N , e ( y , x ) But RSA is 1-way so this task should be hard and the scheme should be x y d mod N If ( x e mod N = y ) then return 1 secure. Return x Else return 0 Correct? Here y 2 Z ⇤ N is the message and x 2 Z ⇤ N is the signature. Mihir Bellare UCSD 13 Mihir Bellare UCSD 14 Security of plain RSA signatures Attacks on plain RSA adversary A ( N , e ) To forge signature of a message y , the adversary, given N , e but not d , Return (1 , 1) must compute y d mod N , meaning invert the RSA function f at y . Adv uf - cma ( A ) = 1 because 1 d ⌘ 1 (mod N ) DS But RSA is 1-way so this task should be hard and the scheme should be secure. adversary A ( N , e ) Pick some distinct y 1 , y 2 2 Z ⇤ N � { 1 } Correct? x 1 Sign ( y 1 ); x 2 Sign ( y 2 ) Return ( y 1 y 2 mod N , x 1 x 2 mod N ) Of course not... Adv uf - cma ( A ) = 1 because ( y 1 y 2 ) d ⌘ y d 1 y d 2 (mod N ) DS Mihir Bellare UCSD 15 Mihir Bellare UCSD 16
DH signatures Other issues When Di ffi e and Hellman introduced public-key cryptography they suggested the DS scheme S ( sk , M ) = D ( sk , M ) V ( pk , M , σ ) = 1 i ff E ( pk , σ ) = M In plain RSA, the message is an element of Z ⇤ N . We really want to be able to sign strings of arbitrary length. where ( E , D ) is a public-key encryption scheme. But • This views public-key encryption as deterministic; they really mean trapdoor permutations in our language • Plain RSA is an example • It doesn’t work! Nonetheless, many textbooks still view digital signatures this way. Mihir Bellare UCSD 17 Mihir Bellare UCSD 18 Throwing in a hash function What we need from H Suppose we have an adversary C that can find a collision for H . Then we Let H : { 0 , 1 } ⇤ ! Z ⇤ N be a public hash function and let pk = ( N , e ) and can break DS via sk = ( N , d ) be the signer’s keys. The hash-then-decrypt scheme is adversary A ( N , e ) Alg S N , d ( M ) Alg V N , e ( M , x ) $ ( M 1 , M 2 ) C σ 1 Sign ( M 1 ) y H ( M ) y H ( M ) x y d mod N If ( x e mod N = y ) then return 1 Return ( M 2 , σ 1 ) Return x Else return 0 This works because H ( M 1 ) = H ( M 2 ) implies M 1 , M 2 have the same signatures: Succinctly, S N , d ( M ) = H ( M ) d mod N σ 1 = S N , d ( M 1 ) = H ( M 1 ) d mod N = H ( M 2 ) d mod N = S N , d ( M 2 ) Di ff erent choices of H give rise to di ff erent schemes. Conclusion : H needs to be collision-resistant Mihir Bellare UCSD 19 Mihir Bellare UCSD 20
RSA PKCS#1 signatures RSA PKCS#1 signatures Signer has pk = ( N , e ) and sk = ( N , d ) where | N | = 1024. Let Signer has pk = ( N , e ) and sk = ( N , d ) where | N | = 1024. Let h : { 0 , 1 } ⇤ ! { 0 , 1 } 160 be a hash function (like SHA1) and let h : { 0 , 1 } ⇤ ! { 0 , 1 } 160 be a hash function (like SHA1) and let n = 1024 / 8 = 128. n = 1024 / 8 = 128. Then Then H PKCS ( M ) = 00 || 01 || FF || . . . || FF || h ( M ) H PKCS ( M ) = 00 || 01 || FF || . . . || FF || h ( M ) | {z } | {z } | {z } | {z } n � 22 20 n � 22 20 And And S N , d ( M ) = H PKCS ( M ) d mod N S N , d ( M ) = H PKCS ( M ) d mod N But first n � 20 = 108 bytes of H PKCS ( M ) are fixed, so H PKCS ( M ) does not look “random.” Mihir Bellare UCSD 21 Mihir Bellare UCSD 22 Full-Domain-Hash (FDH) [BR96] Exercise Let K rsa be a RSA key generator with security parameter k � 2048. Let Signer public key is pk = ( N , e ) and secret key is sk = ( N , d ) the algorithms of signature scheme DS = ( K , S , V ) be defined as follows, with notation explained on the next slide: Alg V N , e ( M , x ) Alg K Alg S N , d ( M ) If ( x e mod N = H ( M )) then return 1 Return H ( M ) d mod N $ ( N , p , q , e , d ) K rsa ; pk ( N , e ); sk ( N , d ) ; Return ( pk , sk ) Else return 0 Alg S N , d ( M ) Alg V N , e ( M , s ) Public hash function H : { 0 , 1 } ⇤ ! Z ⇤ N is defined for example by letting If | M | 6 = 4096 then return ? If | M | 6 = 4096 then return 0 H ( M ) be the first | N | bits of M [1] M [2] M M [1] M [2] M x 1 h 1 i || M [1] ; x 2 h 2 i || M [2] x 1 h 1 i || M [1] ; x 2 h 2 i || M [2] SHA1512(0 8 k M ) k SHA1512(0 7 1 k M ) k · · · y H ( x 1 ) · H ( x 2 ) mod N If s e ⌘ H ( x 1 ) · H ( x 2 ) (mod N ) s y d mod N then return 1 else return 0 . Return s Mihir Bellare UCSD 23 Mihir Bellare UCSD 24
Recommend
More recommend