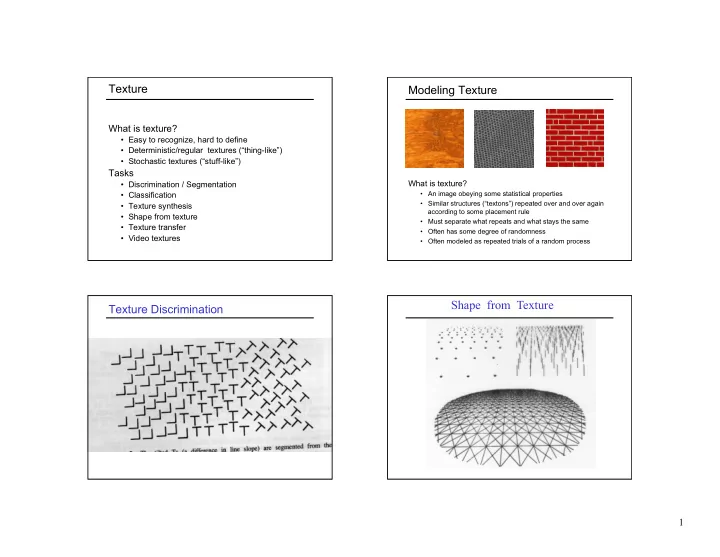

Texture Modeling Texture What is texture? • Easy to recognize, hard to define • Deterministic/regular textures (“thing-like”) • Stochastic textures (“stuff-like”) Tasks What is texture? • Discrimination / Segmentation • An image obeying some statistical properties • Classification • Similar structures (“textons”) repeated over and over again • Texture synthesis according to some placement rule • Shape from texture • Must separate what repeats and what stays the same • Texture transfer • Often has some degree of randomness • Video textures • Often modeled as repeated trials of a random process Shape from Texture Texture Discrimination 1
Texture Texture Synthesis • Goal of texture synthesis: Create new samples of a • Texture is often “stuff” (as opposed to “things”) given texture • Characterized by spatially repeating patterns • Many applications: virtual environments, hole- filling, inpainting, texturing surfaces, image • Texture lacks the full range of complexity of compression photographic imagery, but makes a good starting point for study of image-based techniques radishes rocks yogurt The Challenge Method 1: Copy Blocks of Pixels regular • Need to model the whole spectrum, from regular to Photo stochastic textures stochastic Visual artifacts at block boundaries Pattern Repeated Both? 2
Statistical Modeling of Texture Markov Chain • Assume stochastic model of texture ( Markov • Markov Chain Random Field ) – a sequence of random variables x 1 , x 2 , …, x n • Assume Stationarity : the stochastic model is the – x t is the state of the model at time t same regardless of position in the image x 1 x 2 x 3 x 4 x 5 – Markov assumption : each state is dependent only on the previous one • dependency given by a conditional probability : P ( x t | x t -1 ) – The above is actually a first-order Markov chain – An Nth-order Markov chain: P ( x t | x t -1 , …, x t - n ) stationary texture non-stationary texture Markov Random Field Statistical Modeling of Texture A Markov Random Field (MRF) • Assume stochastic model of texture ( Markov Random Field ) • Generalization of Markov chains to two or more dimensions First-order MRF : • Assume Stationarity : the stochastic model is the • Probability that pixel X takes a certain value given the values same regardless of position of neighbors A , B , C , and D : A • Assume Markov (i.e., local ) property : D X B p(pixel | rest of image) = p(pixel | neighborhood) P ( X | A , B , C , D ) C • Higher-order MRFs have larger neighborhoods, e.g.: ? * * * * * * * * * * * * * X X * * * * * * * 3
Motivation from Language Mark V. Shaney (Bell Labs) • Shannon (1948) proposed a way to generate • Results (using alt.singles corpus): English-looking text using N-grams : – “As I've commented before, really relating to – Assume a Markov model someone involves standing next to impossible.” – Use a large text corpus to compute probability – “One morning I shot an elephant in my arms and distributions of each letter given N –1 previous kissed him.” letters – “I spent an interesting evening recently with a – Starting from a seed, repeatedly sample the grain of salt.” conditional probabilities to generate new letters • Notice how well local structure is preserved! – Can use whole words instead of letters too – Now let’s try this in 2D using pixels Efros & Leung Algorithm Synthesizing One Pixel A. Efros and T. Leung, Texture synthesis by non-parametric sampling, Proc. ICCV , 1999 SAMPLE x sample image Generated image – What is P ( x | neighborhood of pixels around x ) ? – Find all the windows in the image that match the neighborhood • consider only pixels in the neighborhood that are already filled in Idea initially proposed in 1981 (Garber ’81), but dismissed as too – To synthesize pixel x, pick one matching window at random computationally expensive and assign x to be the center pixel of that window 4
Really Synthesizing One Pixel Efros & Leung Algorithm non-parametric sampling SAMPLE x x sample image Input image Generated image Synthesizing a pixel • Assume Markov property, sample from P ( x | Nbr( x )) – An exact neighborhood match might not be present – Building explicit probability tables is infeasible – So we find the best matches using “SSD error” and – Instead, we search the input image for all sufficiently randomly choose between them, preferring better similar neighborhoods and pick one match at random matches with higher probability Computing P ( x | Nbr( x )) Finding Matches • Given output image patch w ( x ) centered • Sum of squared differences (SSD) around pixel x • Find best matching patch in sample image: = ⊂ w arg min d ( w ( x ), w ) I || − || 2 best w sample • Note: normalize d by number of known pixels in w ( x ) • Find all image patches in sample image that are close matches to best patch: or, in Matlab: Ω = < + ε ( x ) { w | d ( w ( x ), w ) ( 1 ) d ( w ( x ), w ) best sum( sum( . − ).^2)) • Compute a histogram of all center pixels in Ω • Histogram = conditional pdf of x 5
Finding Matches Gaussian Filtering • Sum of squared differences (SSD) • The picture shows a smoothing kernel proportional to – Gaussian-weighted to make sure closer neighbors are in better agreement 2 2 + x y − 2 σ 2 e || . * ( .– )|| 2 (which is a reasonable model of a circularly symmetric fuzzy blob) Slide by D.A. Forsyth Details Growing Texture • Random sampling from the set of candidates vs. picking the best candidate • Initialization for blank output image – Start with a “seed” in the middle and grow outward in layers • Hole filling: Growing in “onion skin” order – Starting from the initial configuration, “grow” the texture – Within each “layer”, pixels with the largest number of one pixel at a time known-neighbors are synthesized first – The size of the neighborhood window is a parameter that – Normalize error by the number of known pixels specifies how stochastic the user believes the texture to be – If no close match can be found, the pixel is not – To grow from scratch, we use a random 3 x 3 patch from synthesized until the end input image as seed 6
Varying Window Size Varying Window Size input Increasing window size Synthesis Results Results aluminum wire reptile skin french canvas raffia weave 7
Results Results white bread brick wall wood granite Hole Filling Extrapolation 8
Failure Cases Homage to Shannon Growing “garbage” Verbatim copying Accelerating Texture Synthesis Summary of Efros and Leung Algorithm • Advantages: • For textures with large-scale structure, use a Gaussian – conceptually simple pyramid to reduce required – models a wide range of real-world textures neighborhood size – naturally does hole-filling • Disadvantages: – it’s greedy – it’s slow – it’s heuristic L.-Y. Wei and M. Levoy, "Fast Texture Synthesis using Tree-structured Vector Quantization," SIGGRAPH 2000 9
Another Property of Gaussians Pyramids • Cascading Gaussians : Convolution of a • Useful for representing images at multiple Gaussian with itself is another Gaussian “scales” • Pyramid is built using multiple copies of – So, we can first smooth an image with a small Gaussian image – Then, we convolve that smoothed image with another • Each level in the pyramid is an image with small Gaussian and the result is equivalent to smoothing the original image with a larger Gaussian 1/4 the number of pixels of previous level, – If we smooth an image with a Gaussian having standard i.e., each dimension is 1/2 resolution of 2 σ deviation σ twice, then we get the same result as previous level smoothing the image with a Gaussian having standard deviation √ 2 σ Pyramids 10
Reduce Gaussian Pyramids = ∑ ∑ 2 2 + + g ( u , v ) w ( m , n ) g ( 2 u m , 2 v n ) − l l 1 = − = − m 2 n 2 = g REDUCE [ g ] − l l 1 Expand Gaussian Pyramids − − = ∑ ∑ 2 2 u p v q g ( u , v ) w ( p , q ) g ( , ) − l , n l , n 1 2 2 p = − 2 q = − 2 = g EXPAND [ g ] − l , n l , n 1 11
Convolution Mask Accelerating Texture Synthesis Exploit separability property of Gaussian filtering • For textures with large-scale structure, use a Gaussian − − [ w ( 2 ), w ( 1 ), w ( 0 ), w ( 1 ), w ( 2 )] pyramid to reduce required neighborhood size – Low-resolution image is Commonly used masks: synthesized first – For synthesis at a given pyramid [.05, .25, .4, .25, .4] level, the neighborhood consists of already generated pixels at this level plus all neighboring pixels at or 1/20 [1, 5, 8, 5, 1] the lower-resolution level or 1/16 [1, 4, 6, 4, 1] L.-Y. Wei and M. Levoy, "Fast Texture Synthesis using Tree-structured Vector Quantization," SIGGRAPH 2000 Image Quilting Gaussian Pyramid A. Efros and W. Freeman, Image quilting for texture synthesis and transfer, Proc. SIGGRAPH , 2001 non-parametric sampling High resolution Low resolution p B Input image Synthesizing a block • Observation: neighbor pixels are highly correlated Idea: unit of synthesis = block of pixels • Exactly the same as Efros & Leung but now we want P ( B |Nbr( B )) where B is a block of pixels • Much faster: synthesize all pixels in a block at once 12
Recommend
More recommend