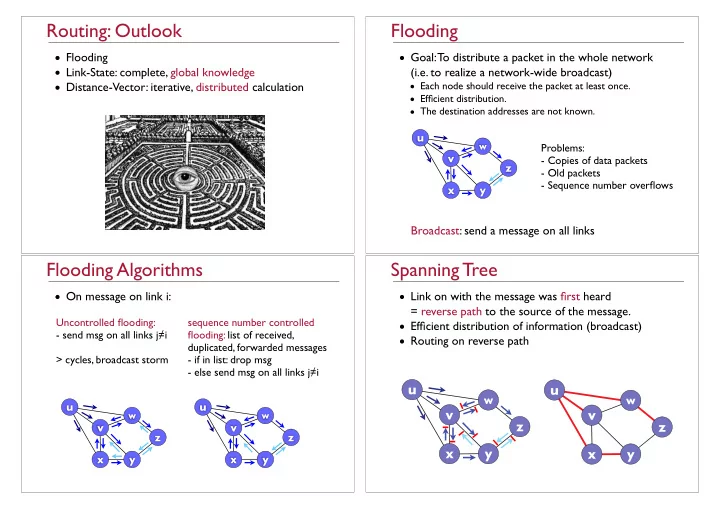
Routing: Outlook Flooding Flooding Goal: To distribute a packet in - PowerPoint PPT Presentation

Routing: Outlook Flooding • Flooding • Goal: To distribute a packet in the whole network • Link-State: complete, global knowledge (i.e. to realize a network-wide broadcast) • Distance-Vector: iterative, distributed calculation • Each node should receive the packet at least once. • Efficient distribution. • The destination addresses are not known. u w Problems: v - Copies of data packets z - Old packets - Sequence number overflows x y Broadcast: send a message on all links Flooding Algorithms Spanning Tree • On message on link i: • Link on with the message was first heard = reverse path to the source of the message. Uncontrolled flooding: sequence number controlled • Efficient distribution of information (broadcast) - send msg on all links j � i flooding: list of received, • Routing on reverse path duplicated, forwarded messages > cycles, broadcast storm - if in list: drop msg - else send msg on all links j � i u u w w u u v v w w z z v v z z x y x y x y x y

Routing Routing: G=(N,E) • Distributed algorithm executed among the routers • Nodes: Routers and u 5 which builds the routing tables Hosts (u,v,w,...) w • Optimization based on routing metric (cost): • Edges: Links between 4 1 2 v delay, hops, congestion, quality, battery, policy, etc. nodes. z 2 • Each edge has a Cost 3 2 • Design and evaluation criteria: associated with it. 3 • Scalability y x - c(u,v) = 1, c(u,x)=2, etc. 1 • Speed of convergence • Stability Main Problem - Calculating the path with the lowest cost from source to destination: D(u,z) = min{path: sum of all edge costs c(.,.) over the path} Link-State Routing Link-State Routing 2 • Assumptions: Each node knows the cost of the link of • Link-State protocols rely on 2 things: - Reliable spreading of link-state information each its directly connected neighbours. (Reliable Flooding) - Calculation of paths from the sum of all the accumulated • Basic Idea: - Every node knows how to reach it’s neighbours. link-state knowledge > e.g., Dijkstra-Algorithm - If this information is spread to every node via flooding, - Notation Dijkstra-Algorithm then every node will have enough information to • D(v): cost of least-cost path from source to v determine the correct path to any node in the network. • p(v): previous node along the current least-cost path In fact, every node will be able to build a complete map of from source to v the network. • N’: subset of nodes; - This means that every node will eventually have access to v is in N’ = least cost from source to v the same information, as every other node. definitively known.

Dijkstra’s Algorithm Dijkstra’s Algorithm Initialisation: Loop: N’ = {u} find m not in N’ such that D(m) is a minimum: for all nodes n add m to N’ if n is a neighbour of u update D(n) for each neighbour n of m and not in N’: then D(n)=c(u,n) D(n) = min(D(n), D(m)+c(m,n)) else D(n)=inf if new D(n): p(n) = m until N’=N step N’ D(v), p(v) D(w), p(w) D(x), p(x) D(y), p(y) D(z), p(z) step N’ D(v), p(v) D(w), p(w) D(x), p(x) D(y), p(y) D(z), p(z) 0 u 1,u 5,u 2,u inf inf Distance-Vector Routing Bellman-Ford Equaltion • Each node knows the cost of the link of each its directly connected neighbours: initial forwarding table. d x ( y ) = min v { c ( x, v ) + d v ( y ) } • Periodically each node transmits their table to all their neighbours. • When a node receives such a table it calculates the v: neighbour of x dx(y): least cost route from x to y as seen from x distance to the nodes on the received table. c(x,v): link cost on link from x to v • If the node discovers a shorter path to a destination node, it’s own table is updated. If the table was updated, the new table is immediately sent to the neighbours, otherwise the node waits for a timeout or a new message.

View of a Node Algorithm • A nodes routing table Routig table for node u: Initialisation (at node s): Notation: consists of triples in the s source for all dest d in N: dest cost nexthop d destination form: <destination, cost, Ds(d) = c(s,d) n neighbour v 1 v for each neighbour n nexthop> Dn(d) = inf for all dest d in N w 3 w send distance vector Ds = [Ds(d): d in N] to n • The messages sent are x 2 x (update)lists containing Loop (at node s): y 3 x tuples in the form: wait (until c(s,n) changes for some neighbour n, or until receive Dn from some neighbour n) z 6 x <destination, cost> for each d in N: Ds(d) = min_n{c(s,n} + Dn(d)} if Ds(d) changed for any destination d send distance vector Ds = [Ds(d): d in N] to all neighbours n Link-Cost Changes Detection of Bad Links • Routers periodically send control packets which have to be acknowledged • Router expects periodic routing updates or Hello messages from its neighbours • Routing oscillations are avoided by k of n rule: a change is only accepted if it persists during at least k 1) y: x=1, z=1 > advertise count-to-infinity problem: 2) z: x=2, y=1 > advertise 1) y: x=6, z=1 LOOP!! of n periods 3) convergence 2) z: x=7, y=1 ... 3) y: x=8, z=1 ... ... 45) z: x=50, y=1 Solution: Poisoned Reverse (partial) z announces Dz(x)=inf if it routes through y to get to x.

Distance-Vector vs. Link-State Different Approaches to Routing • The difference between the two algorithms can be • Proactive vs. reactive routing - proactive: constantly update routing tables for all nodes. summarized: - reactive: find a route on demand (when needed). - D.V.: Each node only talks to its directly connected • Incremental forwarding vs. source routing neighbours, but sends its entire forwarding table. - incremental: routers have a forwarding table specifying the simple to implement, simple to configure, bad convergence, “next hop”. bad scaling. - source routing: the route a packet should take is explicitly - L.S.: Each node talks to all other nodes, but only tells stored in the packet. - loose source routing: only a partial route (subset) is specified. them what it knows for sure (i.e., the state of its directly connected links) fast convergence, generates less traffic, fast reaction on topology changes, bad scaling Summary of Routing Algorithms $ traceroute www.ethz.ch 1 r1.n.it.uu.se (130.238.8.1) 4.772 ms Flooding/Spanning Tree Link-State Distance-Vector 2 l-uu2.uu.se (130.238.6.238) 0.457 ms 3 uu2-fe2.sunet.se (130.242.88.17) 1.364 ms neighbours 4 uppsala2-srp2.sunet.se (130.242.85.162) 2.686 ms “everyone” 5 stockholm2-pos0.sunet.se (130.242.82.33) 4.070 ms 6 se-kth.nordu.net (193.10.252.177) 2.591 ms 7 se-ov.nordu.net (193.10.252.42) 2.916 ms 8 dk-gw2.nordu.net (193.10.68.118) 11.817 ms 9 nordunet.rt1.cop.dk.geant2.net (62.40.124.45) 12.385 ms 10 so-7-3-0.rt1.fra.de.geant2.net (62.40.112.49) 24.939 ms 11 so-6-2-0.rt1.gen.ch.geant2.net (62.40.112.21) 33.028 ms 12 swice2-10ge-1-1.switch.ch (62.40.124.22) 33.212 ms send to: send to: 13 swils2-10ge-1-3.switch.ch (130.59.37.2) 34.002 ms everyone neighbours 14 swiez2-10ge-1-1.switch.ch (130.59.36.206) 37.455 ms • Problem: 15 rou-rz-gw-giga-to-switch.ethz.ch (192.33.92.1) 37.761 ms Does not scale for large networks like the Internet. ... 200 million hosts; network of networks

$ traceroute www.ubs.ch 1 r1.n.it.uu.se (130.238.8.1) 9.989 ms 2 l-uu2.uu.se (130.238.6.238) 0.591 ms 3 uu2-fe2.sunet.se (130.242.88.17) 1.430 ms 4 uppsala2-srp2.sunet.se (130.242.85.162) 1.346 ms 5 stockholm2-pos0.sunet.se (130.242.82.33) 2.607 ms 6 stockholm4-pos0.sunet.se (130.242.82.50) 2.873 ms 7 pos7-7.br1.stk2.alter.net (130.242.94.118) 3.564 ms 8 so-5-0-0.tr2.stk2.alter.net (146.188.6.85) 3.280 ms 9 so-2-0-0.tr2.zur3.alter.net (146.188.3.82) 32.009 ms 10 so-6-0-0.xr2.zur4.alter.net (146.188.5.134) 32.288 ms 11 pos2-0.gw4.zur4.alter.net (146.188.4.194) 31.890 ms 12 ubs-gw.customer.alter.net (146.188.66.170) 33.284 ms ...