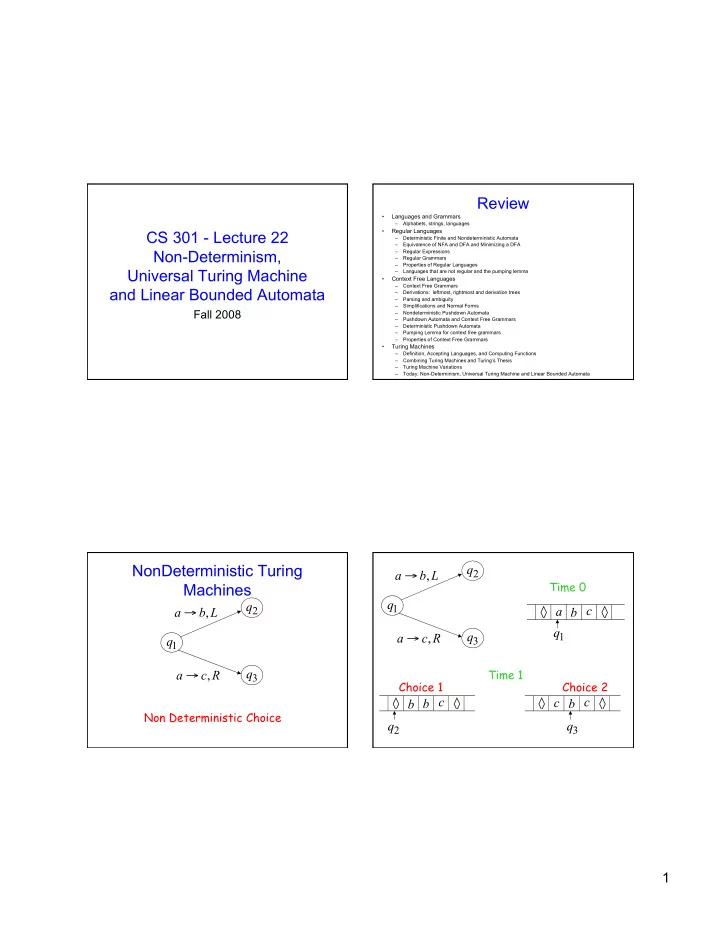
Review Languages and Grammars Alphabets, strings, languages - PDF document

Review • Languages and Grammars – Alphabets, strings, languages • Regular Languages CS 301 - Lecture 22 – Deterministic Finite and Nondeterministic Automata – Equivalence of NFA and DFA and Minimizing a DFA Non-Determinism, – Regular Expressions – Regular Grammars – Properties of Regular Languages Universal Turing Machine – Languages that are not regular and the pumping lemma • Context Free Languages – Context Free Grammars and Linear Bounded Automata – Derivations: leftmost, rightmost and derivation trees – Parsing and ambiguity – Simplifications and Normal Forms Fall 2008 – Nondeterministic Pushdown Automata – Pushdown Automata and Context Free Grammars – Deterministic Pushdown Automata – Pumping Lemma for context free grammars – Properties of Context Free Grammars • Turing Machines – Definition, Accepting Languages, and Computing Functions – Combining Turing Machines and Turing’s Thesis – Turing Machine Variations – Today: Non-Determinism, Universal Turing Machine and Linear Bounded Automata NonDeterministic Turing q a b , L 2 → Time 0 Machines q q 1 a b c 2 a b , L → ◊ ◊ q q 1 a c , R → q 3 1 q Time 1 a c , R → 3 Choice 1 Choice 2 b b c c b c ◊ ◊ ◊ ◊ Non Deterministic Choice q q 2 3 1

w Input string is accepted if NonDeterministic Machines simulate this a possible computation Standard (deterministic) Machines: ∗ q w  x q y 0 f Every deterministic machine is also a nondeterministic machine Initial configuration Final Configuration Final state Deterministic machines simulate NonDeterministic machines: Non-Deterministic Choices q 1 q q 2 3 Deterministic machine: q q Keeps track of all possible computations 4 5 Computation 1 q q 6 7 2

Simulation Non-Deterministic Choices q 1 Deterministic machine: q q 2 3 • Keeps track of all possible computations q q 4 5 • Stores computations in a two-dimensional tape q q 6 7 Computation 2 NonDeterministic machine NonDeterministic machine Time 1 b b c Time 0 Choice 1 ◊ ◊ q q a b , L a b , L → → 2 2 a b c q ◊ ◊ 2 q q 1 1 Choice 2 q c b c ◊ ◊ 1 a c , R a c , R q q → → q 3 3 3 Deterministic machine Deterministic machine # # # # # # # # # # # # a c c # # b b b # # Computation 1 Computation 1 q q # # # # 1 2 # # # # # # # c b c Computation 2 q # # 3 3

Theorem: NonDeterministic Machines have the same power with Repeat Deterministic machines • Execute a step in each computation: • If there are two or more choices in current computation: 1. Replicate configuration 2. Change the state in the replica Remark: The simulation in the Deterministic machine takes time exponential time compared A Universal Turing to the NonDeterministic machine Machine 4

Solution: Universal Turing Machine A limitation of Turing Machines: Turing Machines are “hardwired” Attributes: they execute only one program • Reprogrammable machine • Simulates any other Turing Machine Real Computers are re-programmable Universal Turing Machine Tape 1 Three tapes simulates any other Turing Machine M Description of M Universal Tape 2 Turing Input of Universal Turing Machine: Machine Tape Contents of M Description of transitions of M Tape 3 Initial tape contents of M State of M 5

Tape 1 Alphabet Encoding Description of M … a c b d Symbols: Encoding: 1 11 1111 M 111 We describe Turing machine as a string of symbols: We encode as a string of symbols M State Encoding Transition Encoding … q q q States: q 1 2 3 4 ( q , a ) ( q , b , L ) Transition: δ = 1 2 Encoding: 1 11 1111 111 1 0 1 0 11 0 11 0 1 Encoding: Head Move Encoding Move: L R separator Encoding: 1 11 6

Tape 1 contents of Universal Turing Machine: Machine Encoding M encoding of the simulated machine Transitions: as a binary string of 0’s and 1’s ( q , a ) ( q , b , L ) ( q , b ) ( q , c , R ) δ = δ = 1 2 2 3 Encoding: 1 0 1 0 11 0 11 0 1 00 11 0 1 10 111 0 111 0 11 separator A Turing Machine is described Language of Turing Machines with a binary string of 0’s and 1’s (Turing Machine 1) L = { 010100101, Therefore: (Turing Machine 2) 00100100101111, The set of Turing machines forms a language: …… 111010011110010101, each string of the language is the binary encoding of a Turing Machine …… } 7

How Many Turing Machines Are There? We now have a language L: Each string in L is a Turing Machine! How big is this language? Countable Sets Equivalently… how many Turing machines are there? how many valid Java programs are there? Not finite…. Are there degrees of infinity? Countable set: Infinite sets are either: Countable Any finite set or or Any Countably infinite set: Uncountable There is a one to one correspondence between elements of the set and Natural numbers 8

Example: The set of even integers Example: The set of rational numbers is countable is countable 0 , 2 , 4 , 6 , … Even integers: 1 3 7 , , , … Rational numbers: Correspondence: 2 4 8 1 , 2 , 3 , 4 , … Positive integers: 2 n corresponds to n 1 + Naïve Proof Better Approach 1 1 1 1 1 1 1 , , , … Rational numbers:  1 2 3 1 2 3 4 Correspondence: 2 2 2  1 2 3 Positive integers: 1 , 2 , 3 , … 3 3  Doesn’t work: 1 2 2 2 2 we will never count , , , … 4 numbers with nominator 2:  1 2 3 1 9

1 1 1 1 1 1 1 1   1 2 3 4 1 2 3 4 2 2 2 2 2 2   1 2 3 1 2 3 3 3 3 3   1 2 1 2 4 4   1 1 1 1 1 1 1 1 1 1   1 2 3 4 1 2 3 4 2 2 2 2 2 2   1 2 3 1 2 3 3 3 3 3   1 2 1 2 4 4   1 1 10

1 1 2 1 2 1 1 1 1 , , , , , …  Rational Numbers: 1 2 3 4 1 2 1 3 2 2 2 2  Correspondence: 1 2 3 3 3  1 , 2 , 3 , 4 , 5 , … Positive Integers: 1 2 4  1 We proved: Definition the set of rational numbers is countable S Let be a set of strings by describing an enumeration procedure S An enumeration procedure for is a Turing Machine that generates S all strings of one by one and Each string is generated in finite time 11

s , s , s , … S strings ∈ 1 2 3 Observation: Enumeration output s , s , s , … If for a set there is an 1 2 3 Machine for S (on tape) enumeration procedure, then the set is countable t , t , t , … Finite time: 1 2 3 Naive procedure: Example: Produce the strings in lexicographic order: + { a , b , c } The set of all strings is countable a aa aaa aaaa ...... Proof: Doesn’t work: We will describe an enumeration procedure b strings starting with will never be produced 12

Better procedure: Proper Order a length 1 b c 1. Produce all strings of length 1 aa ab ac 2. Produce all strings of length 2 Produce strings in ba length 2 Proper Order : bb 3. Produce all strings of length 3 bc ca cb 4. Produce all strings of length 4 cc aaa aab length 3 .......... aac ...... Theorem: The set of all Turing Machines Enumeration Procedure: is countable Repeat Proof: Any Turing Machine can be encoded with a binary string of 0’s and 1’s Find an enumeration procedure for the set of Turing Machine strings 13

Linear Bounded Automata (LBAs) are the same as Turing Machines with one difference: Linear Bounded Automata The input string tape space LBAs is the only tape space allowed to use Linear Bounded Automaton (LBA) We define LBA’s as NonDeterministic Input string a b c d e [ ] Working space Open Problem: Left-end Right-end in tape marker marker NonDeterministic LBA’s have same power with Deterministic LBA’s ? All computation is done between end markers 14

Example languages accepted by LBAs: What’s Next n n n • Read L = { a b c } – Linz Chapter 1,2.1, 2.2, 2.3, (skip 2.4), 3, 4, 5, 6.1, 6.2, (skip 6.3), 7.1, 7.2, 7.3, (skip 7.4), 8, 9, 10, 11.1, and 11.2 – JFLAP Chapter 1, 2.1, (skip 2.2), 3, 4, 5, 6, 7, (skip 8), 9, (skip 10), 11.1 • Next Lecture Topics From 11.1 n ! L = { a } – Recursive Languages and Recursively Enumerable Languages • Quiz 3 in Recitation on Wednesday 11/12 – Covers Linz 7.1, 7.2, 7.3, (skip 7.4), 8, and JFLAP 5,6,7 – Closed book, but you may bring one sheet of 8.5 x 11 inch paper with any notes you LBA’s have more power than NPDA’s like. – Quiz will take the full hour • Homework – Homework Due Today LBA’s have also less power – New Homework Available by Friday Morning – New Homework Due Next Thursday than Turing Machines 15