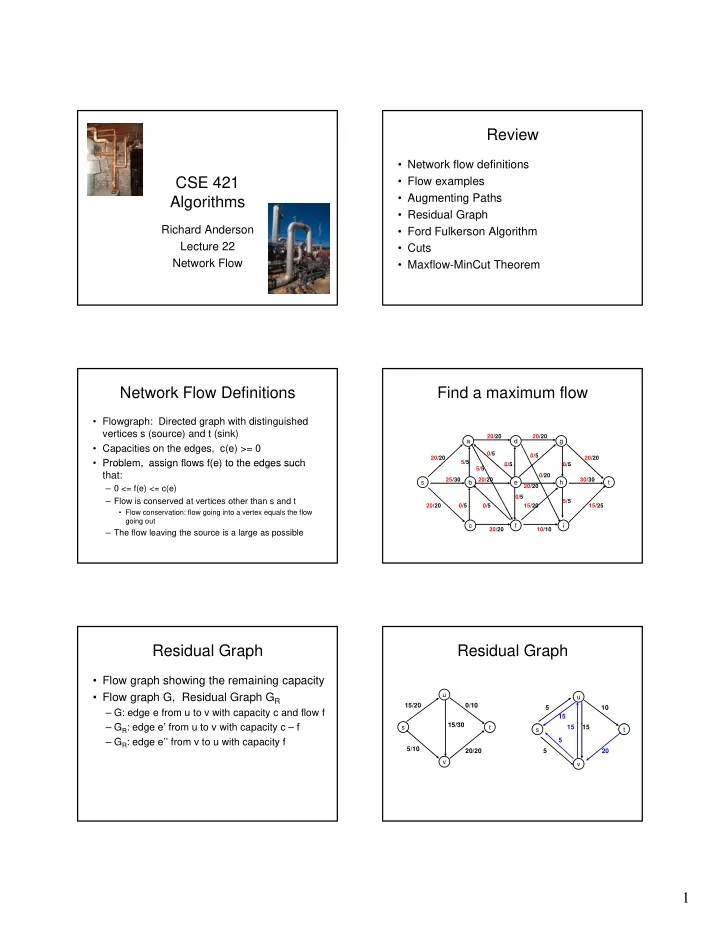
Review Network flow definitions CSE 421 Flow examples - PDF document

Review • Network flow definitions CSE 421 • Flow examples • Augmenting Paths Algorithms g • Residual Graph Richard Anderson • Ford Fulkerson Algorithm Lecture 22 • Cuts Network Flow • Maxflow-MinCut Theorem Network Flow Definitions Find a maximum flow • Flowgraph: Directed graph with distinguished vertices s (source) and t (sink) 20/20 20/20 a d g • Capacities on the edges, c(e) >= 0 0/5 0/5 20/20 20/20 • Problem, assign flows f(e) to the edges such Problem, assign flows f(e) to the edges such 5/5 0/5 0/5 0/5 0/5 5/5 that: 0/20 25/30 20/20 30/30 s b e h t 20/20 – 0 <= f(e) <= c(e) 0/5 – Flow is conserved at vertices other than s and t 5/5 20/20 0/5 0/5 15/20 15/25 • Flow conservation: flow going into a vertex equals the flow going out c f i 20/20 10/10 – The flow leaving the source is a large as possible Residual Graph Residual Graph • Flow graph showing the remaining capacity • Flow graph G, Residual Graph G R u u 15/20 0/10 5 10 – G: edge e from u to v with capacity c and flow f 15 15/30 15/30 – G R : edge e’ from u to v with capacity c – f G d ’ f t ith it f s t 15 15 s t – G R : edge e’’ from v to u with capacity f 5 5/10 20/20 5 20 v v 1

Build the residual graph Augmenting Path Lemma 3/5 • Let P = v 1 , v 2 , …, v k be a path from s to t with d g 2/4 3/3 minimum capacity b in the residual graph. 1/5 1/5 s 1/1 t • b units of flow can be added along the path P in 3/3 the flow graph. g p 2/5 e h 1/1 u u Residual graph: 5 10 15/20 0/10 15 d g 15 15 s t 15/30 s t s t 5 5 20 5/10 20/20 e h v v Proof Ford-Fulkerson Algorithm (1956) • Add b units of flow along the path P while not done • What do we need to verify to show we Construct residual graph G R have a valid flow after we do this? Find an s-t path P in G R with capacity b > 0 – Add b units along in G – If the sum of the capacities of edges leaving S is at most C, then the algorithm takes at most C iterations Cuts in a graph What is Cap(S,T) and Flow(S,T) • Cut: Partition of V into disjoint sets S, T with s in S={s, a, b, e, h}, T = {c, f, i, d, g, t} S and t in T. 20/20 20/20 a d g • Cap(S,T): sum of the capacities of edges from S to T 0/5 0/5 20/20 20/20 5/5 0/5 0/5 • Flow(S,T): net flow out of S Fl (S T) t fl t f S 5/5 0/20 25/30 20/20 30/30 – Sum of flows out of S minus sum of flows into S s b e h t 20/20 0/5 5/5 20/20 0/5 0/10 15/20 15/25 c f i 20/20 10/10 • Flow(S,T) <= Cap(S,T) 2

Minimum value cut Find a minimum value cut u 10 40 6 6 5 8 8 10 s t 10 3 6 t s 2 10 7 40 4 5 v 3 8 5 4 Let S be the set of vertices in G R reachable MaxFlow – MinCut Theorem from s with paths of positive capacity • There exists a flow which has the same value of the minimum cut s u v t • Proof: Consider a flow where the residual graph T S has no s-t path with positive capacity p p p y • Let S be the set of vertices in G R reachable from s with paths of positive capacity s t What can we say about the flows and capacity between u and v? Max Flow - Min Cut Theorem Performance • Ford-Fulkerson algorithm finds a flow • The worst case performance of the Ford- where the residual graph is disconnected, Fulkerson algorithm is horrible hence FF finds a maximum flow. u • If we want to find a minimum cut, we begin 1000 1000 by looking for a maximum flow. 1 s t 1000 1000 v 3

Better methods of finding augmenting paths • Find the maximum capacity augmenting path – O(m 2 log(C)) time algorithm for network flow • Find the shortest augmenting path Find the shortest augmenting path – O(m 2 n) time algorithm for network flow • Find a blocking flow in the residual graph – O(mnlog n) time algorithm for network flow 4