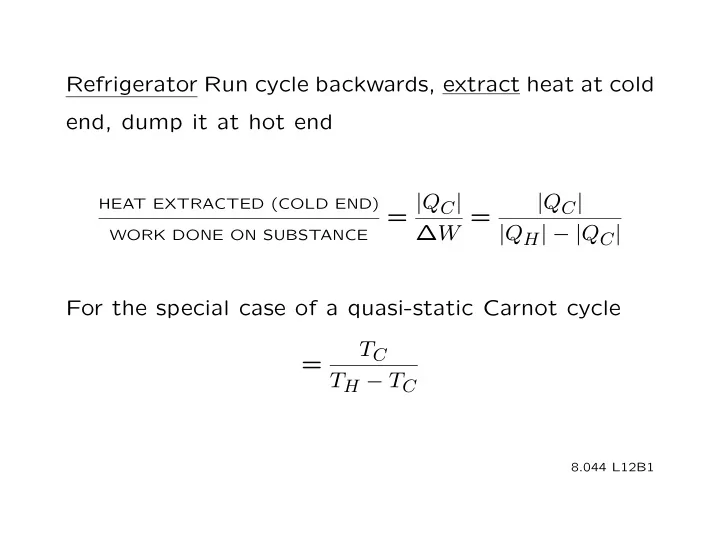
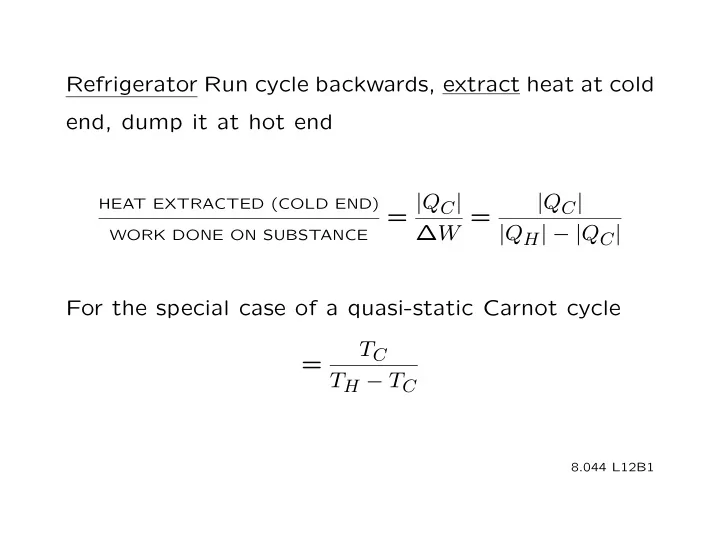
Refrigerator Run cycle backwards, extract heat at cold end, dump it - PowerPoint PPT Presentation

Refrigerator Run cycle backwards, extract heat at cold end, dump it at hot end = | Q C | | Q C | HEAT EXTRACTED (COLD END) ∆ W = | Q H | − | Q C | WORK DONE ON SUBSTANCE For the special case of a quasi-static Carnot cycle T C = T H − T C 8.044 L 12 B1

• As with engine, can show Carnot cycle is optimum. • Practical: increasingly difficult to approach T = 0. • Philosophical: T = 0 is point at which no more heat can be extracted. 8.044 L 12 B2

Heat Pump Run cycle backwards, but use the heat dumped at hot end. WORK DONE ON SUBSTANCE = | Q H | | Q H | HEAT DUMPED (HOT END) ∆ W = | Q H | − | Q C | For the special case of a quasi-static Carnot cycle T H = T H − T C 8.044 L 12 B3

55 o F subsurface temp. at 40 o latitude � T C = 286 K 70 o F room temperature � T H = 294 K 294 | Q H | ∆ W ≤ ∼ 37 8 8.044 L 12 B4

3 rd law lim S = S 0 T � 0 At T = 0 the entropy of a substance approaches a constant value, independent of the other thermody- namic variables. • Originally a hypothesis • Now seen as a result of quantum mechanics Ground state degeneracy g (usually 1) ⇒ S → k ln g (usually 0) 8.044 L 12 B5

∂S Consequences = 0 ∂x T =0 Example: A hydrostatic system 1 1 ∂V ∂S α ≡ = − � 0 as T � 0 V ∂T V ∂P P T V Tα 2 C P − C V = � 0 as T � 0 K T C V ( T → ) T dT → � C V ( T ) � 0 S ( T ) − S (0) = as T � 0 T → T =0 8.044 L 12 B6

Ensembles • Microcanonical: E and N fixed Starting point for all of statistical mechanics Difficult to obtain results for specific systems • Canonical: N fixed, T specified; E varies Workhorse of statistical mechanics • Grand Canonical: T and µ specified; E and N vary Used when the the particle number is not fixed 8.044 L 12 B 7

If the density in phase space depends only on the energy at that point, ρ ( { p , q } ) = ρ ( H{ p , q } ) , carrying out the indicated derivatives shows that ∂ρ = 0 . ∂ t This proves that ρ = ρ ( H{ p , q } ) is a sufficient condition for an equilibrium probability density in phase space. 8.044 L7B2

√   √ p ( p x ) = √ 3 1 − 1 / 2 N e 1 / 2 √ − E/ 2 <E> e e   4 πm 3 N < E > 1 − E/ 2 <E> = √ e 4 πm < E > Now use E = p 2 / 2 m and < E > = < p 2 > / 2 m . x x 1 2 2 − p / 2 <p > p ( p x ) = e x x 2 π < p 2 > x 8.044 L 7 B 17

d) Let Ω ' be the volume in a phase space for N − 1 oscillators of total energy E − t where 2 + ( mω 2 / 2) q i 2 . Since the oscillators are all similar, < t > = E/N = kT . t = (1 / 2 m ) p i Ω ' / Ω p ( p i , q i ) = 2 π N − 1 1 ( E − t ) N − 1 Ω ' = ω ( N − 1)! − 1 N Ω ' 2 π N ! E − t 1 = Ω ω ( N − 1)! E E − t ω N � t � N = 1 − 2 π E − t E ' v- " ' v- " ≈ exp[ − E/<E> ] ≈ <E> − 1 1 p ( p i , q i ) = exp[ − t/ < t > ] (2 π/ω ) < t > 1 exp[ − p i / 2 mkT ] exp[ − ( mω 2 / 2 kT ) q i ] 2 2 = (2 π/ω ) kT � � √ 1 1 2 / 2 mkT ] 2 / 2( kT/mω 2 )] = exp[ − p i exp[ − q i 2 πmkT 2 π ( kT/mω 2 ) = p ( p i ) × p ( q i ) ⇒ p i and q i are S.I. 15

2 1 1 IS THE SUBSYSTEM OF INTEREST. 2, MUCH LARGER, IS THE REMAINDER OR THE "BATH". ENERGY CAN FLOW BETWEEN 1 AND 2. THE TOTAL, 1+2, IS ISOLATED AND REPRESENTED BY A MICROCANONICAL ENSEMBLE. 8.044 L12B8

For the entire system (microcanonical) one has volume of accessible phase space consistent with X p ( system in state X ) = Ω( E ) In particular, for our case p ( { p 1 , q 1 } ) ≡ p ( subsystem at { p 1 , q 1 } ; remainder undetermined ) Ω 1 ( { p 1 , q 1 } )Ω 2 ( E − E 1 ) = Ω( E ) 8.044 L 12 B 9

k ln p ( { p 1 , q 1 } ) = k ln Ω 1 + k ln Ω 2 ( E − E 1 ) − k ln Ω( E ) v v v k ln 1 = 0 S 2 ( E − E 1 ) S ( E ) ∂S 2 ( E 2 ) S 2 ( E − E 1 ) ≈ S 2 ( E ) − E 1 ∂E 2 v evaluated at E 2 = E 8.044 L 12 B 10

H 1 ( { p 1 , q 1 } ) k ln p ( { p 1 , q 1 } ) = − + S 2 ( E ) − S ( E ) T v v The first term on the right depends on the specific state of the subsystem. The remaining terms on the right depend on the reser- voir and the average properties of the subsystem. 8.044 L 12 B 11

In all cases, including those where the system is too small for thermodynamics to apply, H 1 ( { p 1 , q 1 } ) p ( { p 1 , q 1 } ) � exp[ − ] kT H 1 ( { p 1 , q 1 } ) exp[ − ] kT = H 1 ( { p 1 , q 1 } ) � exp[ − ] { dp 1 , dq 1 } kT 8.044 L 12 B 12

If thermodynamics does apply, one can go further. S ( E ) = S 1 ( < E 1 > ) + S 2 ( < E 2 > ) S 2 ( E ) − S ( E ) = S 2 ( E ) − S 2 ( < E 2 > ) − S 1 ( < E 1 > ) , k j ≈ ( ∂S 2 ( E 2 ) /∂E 2 ) < E 1 > = < E 1 > /T H 1 ( { p 1 , q 1 } ) < E 1 > k ln p ( { p 1 , q 1 } ) = − + − S 1 T T ( < E 1 > − TS 1 ) H 1 ( { p 1 , q 1 } ) p ( { p 1 , q 1 } ) = exp[ ] exp[ − ] kT kT , k j ≡ 1 /Zh α 8.044 L12B13

< E 1 > − TS 1 = U 1 − T 1 S 1 = F 1 H ( { p, q } ) p ( { p, q } ) = ( Zh α ) − 1 exp[ − ] kT Z is called the partition function. H ( { p, q } ) � ] { dp, dq } /h α Z ( T, V, N ) = exp[ − kT ( E − TS ) F ( T, V, N ) = exp[ − ] = exp[ − ] kT kT 8.044 L12B14

In the canonical ensemble, the partition function is the source of thermodynamic information. F ( T, N ) = − kT ln Z N ( T, V ) V, ∂F S ( T, V, N ) = − ∂T V,N ∂F P ( T, V, N ) = − ∂V T,N 8.044 L 12 B 15

MIT OpenCourseWare http://ocw.mit.edu 8.044 Statistical Physics I Spring 2013 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.