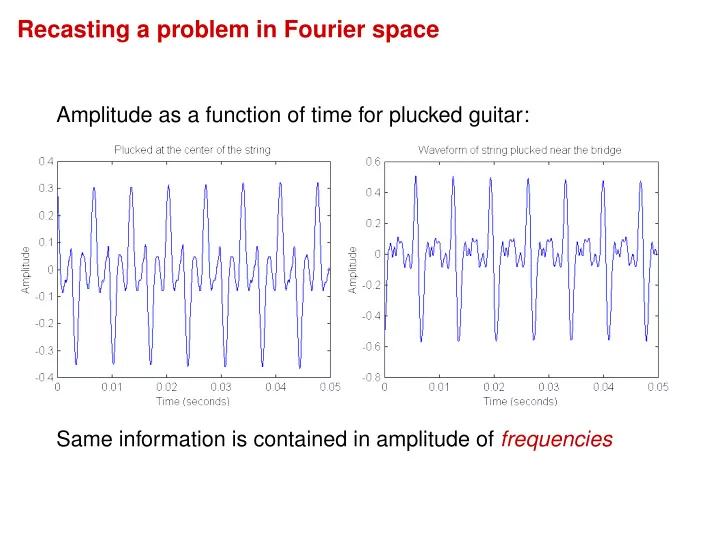
Recasting a problem in Fourier space Amplitude as a function of time - PowerPoint PPT Presentation

Recasting a problem in Fourier space Amplitude as a function of time for plucked guitar: Same information is contained in amplitude of frequencies

Energy by adding up frequencies/wavelengths Describe energy by where particle is and how fast it is moving or by adding up energy in each wavelength given the distribution of wavelengths

2D Fourier transforms of images

Expanding wave functions in an HO basis V @ r D 15 Single-particle radial wf ψ ( r ) Expand in harmonic oscillator wfs: 10 E exact' =')1.51' N max � 5 ψ N max ( r ) = c α φ α ( r ) ]= α = 0 2.5 r 0.5 1.0 1.5 2.0 Find c α s by diagonalizing � H Ψ = E Ψ - 5 ψ exact ( r ) , ψ 0 ( r ) , 0 . 5 ∗ φ 0 ψ exact ( r ) , ψ 0 ( r ) , 0 . 5 ∗ φ 0 wf wf 2.5 2.5 2.0 2.0 1.5 1.5 ]= 1.0 1.0 0.5 0.5 2.5 r 2.5 r 0.5 1.0 1.5 2.0 0.5 1.0 1.5 2.0 - 0.5 - 0.5 N max = 0, E 0 = − 1 . 30 N max = 0, E 0 = + 5 . 23

Expanding wave functions in an HO basis V @ r D 15 Single-particle radial wf ψ ( r ) Expand in harmonic oscillator wfs: 10 E exact' =')1.51' N max � 5 ψ N max ( r ) = c α φ α ( r ) ]= α = 0 2.5 r 0.5 1.0 1.5 2.0 Find c α s by diagonalizing � H Ψ = E Ψ - 5 ψ exact ( r ) , ψ 2 ( r ) , 0 . 5 ∗ φ 2 ψ exact ( r ) , ψ 2 ( r ) , 0 . 5 ∗ φ 2 wf wf 2.5 2.5 2.0 2.0 1.5 1.5 ]= 1.0 1.0 0.5 0.5 2.5 r 2.5 r 0.5 1.0 1.5 2.0 0.5 1.0 1.5 2.0 - 0.5 - 0.5 N max = 2, E 2 = − 1 . 46 N max = 2, E 2 = − 0 . 87

Expanding wave functions in an HO basis V @ r D 15 Single-particle radial wf ψ ( r ) Expand in harmonic oscillator wfs: 10 E exact' =')1.51' N max � 5 ψ N max ( r ) = c α φ α ( r ) ]= α = 0 2.5 r 0.5 1.0 1.5 2.0 Find c α s by diagonalizing � H Ψ = E Ψ - 5 ψ exact ( r ) , ψ 4 ( r ) , 0 . 2 ∗ φ 4 ψ exact ( r ) , ψ 4 ( r ) , 0 . 2 ∗ φ 4 wf wf 2.5 2.5 2.0 2.0 1.5 1.5 ]= 1.0 1.0 0.5 0.5 2.5 r 2.5 r 0.5 1.0 1.5 2.0 0.5 1.0 1.5 2.0 - 0.5 - 0.5 N max = 4, E 4 = − 1 . 46 N max = 4, E 4 = − 1 . 04

Expanding wave functions in an HO basis V @ r D 15 Single-particle radial wf ψ ( r ) Expand in harmonic oscillator wfs: 10 E exact' =')1.51' N max � 5 ψ N max ( r ) = c α φ α ( r ) ]= α = 0 2.5 r 0.5 1.0 1.5 2.0 Find c α s by diagonalizing � H Ψ = E Ψ - 5 ψ exact ( r ) , ψ 6 ( r ) , 0 . 2 ∗ φ 6 ψ exact ( r ) , ψ 6 ( r ) , 0 . 2 ∗ φ 6 wf wf 2.5 2.5 2.0 2.0 1.5 1.5 ]= 1.0 1.0 0.5 0.5 2.5 r 2.5 r 0.5 1.0 1.5 2.0 0.5 1.0 1.5 2.0 - 0.5 - 0.5 N max = 6, E 6 = − 1 . 50 N max = 6, E 6 = − 1 . 40

Expanding wave functions in an HO basis V @ r D 15 Single-particle radial wf ψ ( r ) Expand in harmonic oscillator wfs: 10 E exact' =')1.51' N max � 5 ψ N max ( r ) = c α φ α ( r ) ]= α = 0 2.5 r 0.5 1.0 1.5 2.0 Find c α s by diagonalizing � H Ψ = E Ψ - 5 Extend to many-body system ψ exact ( r ) , ψ 8 ( r ) , 0 . 2 ∗ φ 8 ψ exact ( r ) , ψ 8 ( r ) , 0 . 2 ∗ φ 8 wf wf 2.5 2.5 2.0 2.0 1.5 1.5 ]= 1.0 1.0 0.5 0.5 2.5 r 2.5 r 0.5 1.0 1.5 2.0 0.5 1.0 1.5 2.0 - 0.5 - 0.5 N max = 8, E 8 = − 1 . 50 N max = 8, E 8 = − 1 . 43