r
play

R A B Relational Mapping b 1 Properties b 2 a 1 (Archery) a 2 b - PDF document

Jan 05, 2024 •265 likes •331 views

Binary relation R from A to B codomain domain R A B Relational Mapping b 1 Properties b 2 a 1 (Archery) a 2 b 3 a 3 b 4 arrows lec 3W.1 lec 3W.2 Albert R Meyer February 22, 2012 Albert R Meyer February 22, 2012 function archery

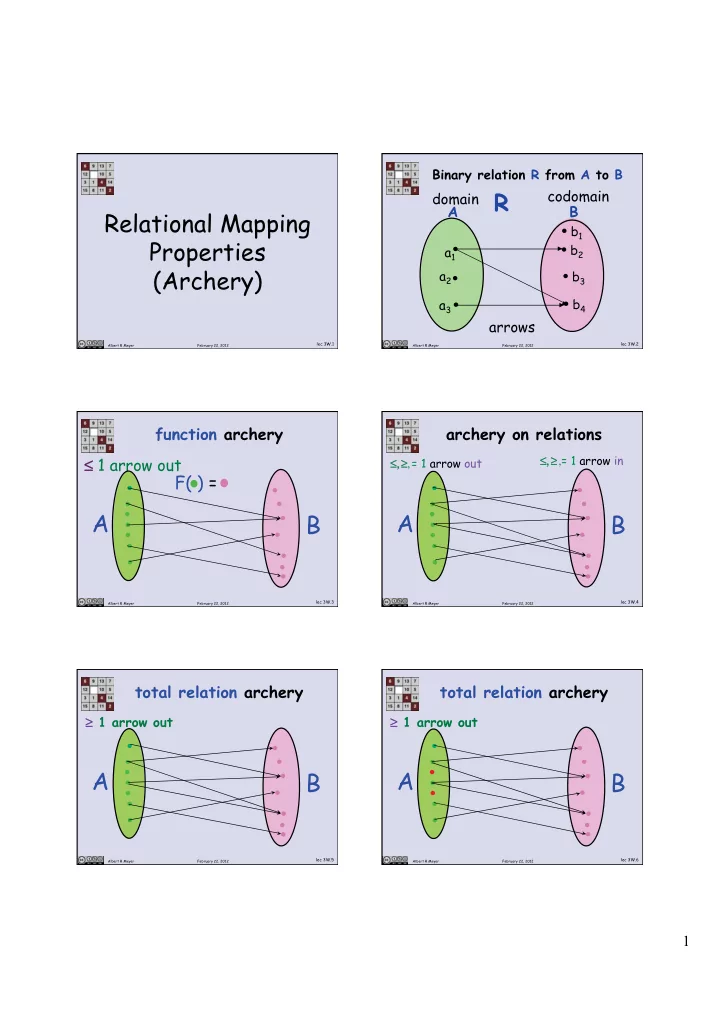
  1. Binary relation R from A to B codomain domain R A B Relational Mapping b 1 Properties b 2 a 1 (Archery) a 2 b 3 a 3 b 4 arrows lec 3W.1 lec 3W.2 Albert R Meyer February 22, 2012 Albert R Meyer February 22, 2012 function archery archery on relations ≤, ≥ , = 1 arrow in ≤, ≥ ≤ 1 arrow out , = 1 arrow out ≤, ≥ ≤, ≥ F( ) = A A B B lec 3W.3 lec 3W.4 Albert R Meyer February 22, 2012 Albert R Meyer February 22, 2012 total relation archery total relation archery 1 arrow out 1 arrow out ≥ ≥ A A B B lec 3W.5 lec 3W.6 Albert R Meyer February 22, 2012 Albert R Meyer February 22, 2012 1

  2. total relation archery total relation 1 arrow out ≥ R is total iff A = R − 1 B ( ) A B lec 3W.7 lec 3W.8 Albert R Meyer February 22, 2012 Albert R Meyer February 22, 2012 g : R × R → R total & function archery 1 g(x, y) :: = exactly 1 arrow out x − y F( ) = domain(g) = all pairs of reals A codomain(g) = all reals B But g is not total: g(r,r) not defined lec 3W.9 lec 3W.10 Albert R Meyer February 22, 2012 Albert R Meyer February 22, 2012 0 :D → R g surjection archery 1 g 0 (x, y) :: = 1 arrow in ≥ x − y D :: = R 2 − (x, y)|x = y { } where A B g 0 , g have the same graph, different domains g 0 is total lec 3W.11 lec 3W.12 Albert R Meyer February 22, 2012 Albert R Meyer February 22, 2012 2

  3. surjection archery surjection archery 1 arrow in 1 arrow in ≥ ≥ A A B B lec 3W.13 lec 3W.14 Albert R Meyer February 22, 2012 Albert R Meyer February 22, 2012 surjection injection archery ≤ 1 arrow in R is a surjection iff ( ) = B R A A B lec 3W.15 lec 3W.16 Albert R Meyer February 22, 2012 Albert R Meyer February 22, 2012 injection archery injection archery ≤ 1 arrow in ≤ 1 arrow in A A B B lec 3W.17 lec 3W.18 Albert R Meyer February 22, 2012 Albert R Meyer February 22, 2012 3

  4. bijection archery Mapping Rule (bij) exactly 1 arrow out exactly 1 arrow in A bijection from f( ) = A to B implies |A| = |B| A B for finite A, B lec 3W.19 lec 3W.20 Albert R Meyer February 22, 2012 Albert R Meyer February 22, 2012 4

  5. MIT OpenCourseWare http://ocw.mit.edu 6.042J / 18.062J Mathematics for Computer Science Spring 20 15 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.

Recommend

More recommend