Program Analysis Techniques: System Zoo’s Perspective Kwangkeun Yi Programming Research Laboratory ropas.snu.ac.kr SNU/KAIST 8/18/2003 @ LiComR Workshop, SonggwangSa Temple
✷ Open Problem automatic checking of bugs in softwares 1
✷ 50-year Achievements (1/2) 1st generation: syntax analysis • lexical analysis & parsing: 1+*^^* • checking in ∼ 10 4 lines/sec • context-free-grammar languages 2
✷ 50-year Achievements (2/2) 2nd generation: type checking/inference • simple typing, polymorphic typing, sub-typing: 1+’’a’’ • inferencing in ∼ 10 3 lines/sec • HOT(higher-order & typed) languages (v.s. C, C++) 3
✷ Need 3rd Gen. Debugging Technolgy • correct programs in both syntax and type can still be incorrect . • 1+2 : correct in syntax and type, but does not compute 12 (our expectation) 4
✷ Not Yet in 3rd Generation • barely effective the-status-quo: testing, run-chase, code re- view, field manual, etc. • not automatic, losing performance – AT&T: productivity = 10 lines/month (1995) – ETRI: 1-character bug/2 months (2000) – On-line game .com’s: 24-hr monitoring under junk food 5
✷ Badly Need 3rd Gen. Technology impossible/difficult for manual debbugging • complicated ∞ , large ∞ softwares • cost: big, low product quality – recall k × million cars/zipels/phones? – Sony mobile phone: recall 420,000 units, 120 million dol- lars, 2001 – Ariane rocket: 500 million dollars, 2 billion dollars, 1996 6
✷ Position of Program Analysis • 1st gen.(1970s): syntax analysis • 2nd gen.(1990s): type checking/inference • 3rd gen.(2000s): program analysis 7
✷ Program Analysis is statically understanding program behaviors 8
✷ Facts about Program Analysis • in principle: it’s impossible • in practice: it’s impressive • wisdom: sound approximation, goal-specific accuracy-cost tradeoff, make use of statistics in programs 9
✷ Impressive Examples not toys • check for deadlock [CT95] • check for overflow [Gu97] • check for un-handled exceptions [YiRy97] • check for resource requirements [Ba01] 10
• check for out-of-range buffer indices [CT03] • transform memory allocation behavior [LeYaYi03] • and many more
✷ Program Analysis a technology for static, automatic, and safe estimation of pro- gram’s run-time behaviors • “static”: before execution • “automatic”: program analyzes programs • “safe”: result must cover the reality • “estimation”: cannot be exact in principle “static analysis”, “abstract interpretation”, “data flow analysis”, “model checking”, “type system”, (“program proof”) 11
✷ Obvious: Rising Industry Interest • s/w companies experienced big failure • they will ask/look for program analysis • need be ready for the opportunity • other apps too: s/w understanding, s/w optimization 12
✷ Talk Outline • program analysis frameworks and their roles • one style: interpreter-based analysis • another style: constraint-based analysis • a mixed style • program analyzer generator Zoo 13
✷ Program Analysis Frameworks • abstract interpretation [CC77,CC92a,CC95b] • conventional data flow analysis [KU76,KU77,He77,RP86] • constraint-based analysis [He92,AH95] • model checking [CGP99] 14
✷ Use of Each Framework • design/specification frameworks - abstract interpretation - data flow analysis - constraint-based analysis • query about analysis result - model checking : computation-tree-logic(CTL) formula over analysis results 15
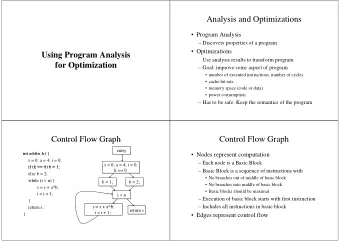
✷ Every Program Analysis Given a program • step 1: set-up equations • step 2: solve the equations – solution = graph � abstract program states, flows � • step 3: make sense of the solution – checking some properties = model checking 16
✷ One Style: Abstract Interpretation Skeleton for Semantic(Data Flow) Equations Program to analyze: ::= integer/variable e z | x primitive operation | e 1 + e 2 assignment | x := e | e ; e sequence | if e 1 e 2 e 3 choice 17
Abstract semantics: s ∈ State = Var → Sign E ∈ Expr × State → Sign × State E ( z, s ) = (ˆ z, s ) E ( x, s ) = ( s ( x ) , s ) E ( x := e, s ) = let ( v 1 , s 1 ) = E ( e, s ) in ( v 1 , s 1 [ v 1 /x ]) E ( e 1 ; e 2 , s ) = let ( v 1 , s 1 ) = E ( e 1 , s ) ( v 2 , s 2 ) = E ( e 2 , s 1 ) in ( v 2 , s 2 ) E ( e 1 + e 2 , s ) = let ( v 1 , s 1 ) = E ( e 1 , s ) ( v 2 , s 2 ) = E ( e 2 , s 1 ) in ( add ( v 1 , v 2 ) , s 2 ) E ( if e 1 e 2 e 3 , s ) = let ( v 1 , s 1 ) = E ( e 1 , s ) ( v 2 , s 2 ) = E ( e 2 , s 1 ) ( v 3 , s 3 ) = E ( e 3 , s 1 ) in ( v 2 , s 2 ) ⊔ ( v 3 , s 3 )
△ [ [ E ] ] = fix F where F : ( Expr × State → Sign × State ) → ( Expr × State → Sign × State ) △ where F ( E ) = λ ( e, s ) . case e of z : ((ˆ z ) , s ) x : ( s ( x ) , s ) x := e : · · · E ( e, s ) · · · e 1 ; e 2 : · · · E ( e 1 , s ) · · · E ( e 2 , s 1 ) · · · · · ·
✷ Correctness Analysis designer has to prove: α ← − fix F fix F − → γ where fix F = [ [ E ] ] and fix F = [ [ E ] ] of F ∈ ( Expr × State → Sign × State ) → ( Expr × State → Sign × State ) F ∈ ( Expr × S tate → I nt × S tate ) → ( Expr × S tate → I nt × S tate ) 18
✷ Analyzer Sets-up Equations from Programs 0 � �� � x := 1; y := x+1 � �� � � �� � 1 2 X ↓ X ↑ i ∈ State i ∈ Sign × State X ↓ X ↑ X ↑ = = ⊤ 0 0 2 X ↓ X ↓ X ↑ ( X ↑ X ↑ 1 a . 2[ X ↑ = = 1 a . 1 , 1 a . 1 /x ]) 1 0 1 X ↓ X ↑ X ↑ ( X ↑ X ↑ 2 a . 2[ X ↑ = 1 . 2 = 2 a . 1 , 2 a . 1 /y ]) 2 2 X ↓ X ↓ X ↑ ( add ( X ↓ X ↓ = = 2 . 2( x ) , 1) , 2 . 2) 2 a 2 2 a 19
✷ Analyzer Solves the Equations X ↓ X ↓ 1 1 . . . . . . X ↓ X ↓ n n = F X ↑ X ↑ 1 1 . . . . . . X ↑ X ↑ n n Solving F 2 ⊥ , · · · • ⊥ , F ⊥ , ⊥ ⊕ F ⊥ ⊕ F 2 ⊥ , · · · • ⊥ , ⊥ ⊕ F ⊥ , 20
✷ A Solution = (Fixpoint, Flow Graph) Fixpoint: equation solution ( X ↓ i , X ↑ i ). Flow graph: X ↑ X ↑ ← 0 2 X ↓ X ↓ X ↑ X ↑ ← ← 1 0 1 1 a X ↓ X ↑ X ↑ X ↑ ← 1 . 2 ← 2 2 2 a X ↓ X ↓ X ↑ X ↓ ← ← 2 a 2 2 a 2 21
✷ Query on Solution about Program Properties Model checking • model = the flow graph • formula = CTL formula – modality = { A , E } × { G , F , X , U } – body = first-order predicate over X ↓ i and X ↑ i Query examples: X ↑ i ∈ Sign × State 22
• Does variable v remain positive? AG ( v = ⊕ ) • Can variable v be positive? EF ( v = ⊕ ) • Does variable v remain positive until w is negative? AU ( v = ⊕ , w = � ) May query at a particular program point: • annotate program text with CTL formula
– “From here, does variable v remain positive?” v := x+y; ## AG(v= ⊕ ) if v > 0 then v := v-2 else v := v+1; ...
✷ Higher-order Case: Analyzing Java or ML Programs Program: e ::= x variable | λx.e abstraction | e 1 e 2 application Abstract semantics: ∈ State = Var → 2 Expr s ∈ Expr × State → 2 Expr E 23
E ( x, s ) = s ( x ) E ( λx.e, s ) = { λx.e } = let { λx i .e ′ E ( e 1 e 2 , s ) i } = E ( e 1 , s ) v = E ( e 2 , s ) in ⊔ i E ( e ′ i , s ⊔ { x i �→ v } )
✷ Analyzer Sets-up Equations from Programs X ↓ X ↑ i ∈ 2 Expr i ∈ State X ↓ X ↑ X ↑ = ⊥ = ⊔ λx i .e i ∈ X ↑ e i 0 0 0 1 � �� � 3 X ↓ X ↓ X ↑ ���� = = ( λx.x 1) ( λx. x 1) ( λy.y ) 1 0 1 � �� � � �� � 1 2 X ↓ X ↓ X ↑ = = ( λy.y ) 2 0 2 e i = X ↓ 0 ⊔ { x i �→ X ↑ for each λx i .e i ∈ X ↑ X ↓ 2 } 1 24
✷ Solution: Fixpoint and Flow Graph As before, except that equations/flow edges are generated during fixpoint computation: X ↑ X ↑ 3 ⊔ X ↑ = 0 2 a X ↓ X ↓ 0 ⊔ { x �→ X ↑ generated equations = 2 } 3 while solving X ↓ X ↓ 0 ⊔ { x �→ X ↑ = 2 } 2 a 25
✷ Another Style: Constraint-based Analysis A high-level skeleton for data flow equations • setting-up constraints • propagating constraints (constraint closure) • solution: either – the set of “atomic” constraints, or – solution/model of the “atomic” constraints 26
✷ Naive Style Example Program: ::= variable e x abstraction | λx.e application | e 1 e 2 Constraint set: X ⊃ se se ::= lam( x, e ) atomic | app( X, X ) | X ∈ 2 Expr at each expr or var X 27
Setting-up constraints: e ′ ⊢ C λx.e ′ ⊢ { X e ⊃ lam( x, e ′ ) } ∪ C x ⊢ {} e 1 ⊢ C 1 e 2 ⊢ C 2 e 1 e 2 ⊢ { X e ⊃ app( X e 1 , X e 2 ) } ∪ C 1 ∪ C 2
✷ Solution: Fixpoint and Flow Graph By the constraint propagation(closure) rules: X a ⊃ app( X b , X c ) , X b ⊃ lam( x, e ) X a ⊃ X e , X x ⊃ X c X a ⊃ X b , X b ⊃ atomic X a ⊃ atomic • Solution: atomic constraints of X e ⊃ lam( x, e ) from the clo- sure • Flow graph: X e ← X e ′ iff X e ⊃ X e ′ 28
Recommend
More recommend
