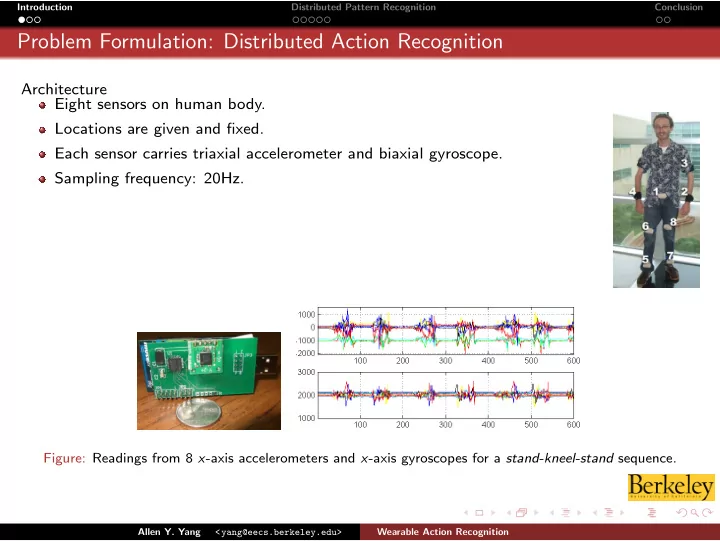

Introduction Distributed Pattern Recognition Conclusion Problem Formulation: Distributed Action Recognition Architecture Eight sensors on human body. Locations are given and fixed. Each sensor carries triaxial accelerometer and biaxial gyroscope. Sampling frequency: 20Hz. Figure: Readings from 8 x -axis accelerometers and x -axis gyroscopes for a stand-kneel-stand sequence. Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Challenges Simultaneous segmentation and classification. 1 Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Challenges Simultaneous segmentation and classification. 1 Individual sensors not sufficient to classify full-body motions. 2 Single sensors on the upper body can not recognize lower body motions. Vice Versa. Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Challenges Simultaneous segmentation and classification. 1 Individual sensors not sufficient to classify full-body motions. 2 Single sensors on the upper body can not recognize lower body motions. Vice Versa. Simulate sensor failure and network congestion by different subsets of active sensors. 3 Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Challenges Simultaneous segmentation and classification. 1 Individual sensors not sufficient to classify full-body motions. 2 Single sensors on the upper body can not recognize lower body motions. Vice Versa. Simulate sensor failure and network congestion by different subsets of active sensors. 3 Identity independence : 4 Figure: Same actions performed by two subjects. Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Challenges Simultaneous segmentation and classification. 1 Individual sensors not sufficient to classify full-body motions. 2 Single sensors on the upper body can not recognize lower body motions. Vice Versa. Simulate sensor failure and network congestion by different subsets of active sensors. 3 Identity independence : 4 Figure: Same actions performed by two subjects. Proposed solutions: 10-D LDA feature space suffices to express 12 action classes on individual motes. 1 Individual sensor obtains limited classification ability. 2 To save power, sensors become active only when certain events are locally detected. Global classifier adapts to change of active sensors in network. 3 Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Experiment Results Precision vs Recall: Sensors 2 7 2,7 1,2,7 1- 3, 7,8 1- 8 Prec [%] 89.8 94.6 94.4 92.8 94.6 98.8 Rec [%] 65 61.5 82.5 80.6 89.5 94.2 Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Experiment Results Precision vs Recall: Sensors 2 7 2,7 1,2,7 1- 3, 7,8 1- 8 Prec [%] 89.8 94.6 94.4 92.8 94.6 98.8 Rec [%] 65 61.5 82.5 80.6 89.5 94.2 Segmentation results using all 8 sensors: (a) Stand-Sit-Stand (b) Sit-Lie-Sit (c) Rotate-Left (d) Go-Downstairs Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Mixture Subspace Model for Distributed Action Recognition Training samples : manually segment and normalize to duration h . 1 Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Mixture Subspace Model for Distributed Action Recognition Training samples : manually segment and normalize to duration h . 1 On each sensor node i , stack training actions into vector form 2 v i = [ x (1) , · · · , x ( h ) , y (1) , · · · , y ( h ) , z (1) , · · · , z ( h ) , θ (1) , · · · , θ ( h ) , ρ (1) , · · · , ρ ( h )] T ∈ R 5 h Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Mixture Subspace Model for Distributed Action Recognition Training samples : manually segment and normalize to duration h . 1 On each sensor node i , stack training actions into vector form 2 v i = [ x (1) , · · · , x ( h ) , y (1) , · · · , y ( h ) , z (1) , · · · , z ( h ) , θ (1) , · · · , θ ( h ) , ρ (1) , · · · , ρ ( h )] T ∈ R 5 h Full body motion 3 � v 1 y 1 � . . ∈ R 8 · 5 h Training sample: v = Test sample: y = . . . . v 8 y 8 Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Mixture Subspace Model for Distributed Action Recognition Training samples : manually segment and normalize to duration h . 1 On each sensor node i , stack training actions into vector form 2 v i = [ x (1) , · · · , x ( h ) , y (1) , · · · , y ( h ) , z (1) , · · · , z ( h ) , θ (1) , · · · , θ ( h ) , ρ (1) , · · · , ρ ( h )] T ∈ R 5 h Full body motion 3 � v 1 y 1 � . . ∈ R 8 · 5 h Training sample: v = Test sample: y = . . . . v 8 y 8 Action subspace : If y is from Class i , 4 y 1 � v 1 � v 1 � � . . . = α i , 1 y = . . + · · · + α i , n i . = A i α i . . . . y 8 v 8 v 8 1 n i Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Sparse Representation Nevertheless, label( y ) = i is the unknown membership function to solve: 1 α 1 α 2 = A x ∈ R 8 · 5 h . Sparse Representation: y = � A 1 · · · � A 2 A K . . . α K Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Sparse Representation Nevertheless, label( y ) = i is the unknown membership function to solve: 1 α 1 α 2 = A x ∈ R 8 · 5 h . Sparse Representation: y = � A 1 · · · � A 2 A K . . . α K i , 0 , · · · , 0] T . One solution: x = [0 , 0 , · · · , α T 2 Sparse representation encodes membership. Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Sparse Representation Nevertheless, label( y ) = i is the unknown membership function to solve: 1 α 1 α 2 = A x ∈ R 8 · 5 h . Sparse Representation: y = � A 1 · · · � A 2 A K . . . α K i , 0 , · · · , 0] T . One solution: x = [0 , 0 , · · · , α T 2 Sparse representation encodes membership. Two problems : 3 Directly solving the linear system is intractable. Seeking the sparsest solution. Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Dimensionality Reduction Construct Fisher/LDA features R i ∈ R 10 × 5 h on each node: 1 y i = R i y i = R i A i x = ˜ A i x ∈ R 10 ˜ Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Dimensionality Reduction Construct Fisher/LDA features R i ∈ R 10 × 5 h on each node: 1 y i = R i y i = R i A i x = ˜ A i x ∈ R 10 ˜ Globally 2 ˜ y 1 y 1 R 1 ··· 0 . . . . = RA x = ˜ = ... A x ∈ R 8 · 10 . . . . . . . . y 8 ˜ y 8 0 ··· R 8 Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Dimensionality Reduction Construct Fisher/LDA features R i ∈ R 10 × 5 h on each node: 1 y i = R i y i = R i A i x = ˜ A i x ∈ R 10 ˜ Globally 2 ˜ y 1 y 1 R 1 ··· 0 . . . . = RA x = ˜ = ... A x ∈ R 8 · 10 . . . . . . . . y 8 ˜ y 8 0 ··· R 8 During the transformation, the data matrix A and x remain unchanged . 3 Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Seeking Sparsest Solution: ℓ 1 -Minimization Ideal solution: ℓ 0 -minimization 1 x ∗ = arg min y = ˜ ( P 0 ) � x � 0 s.t. ˜ A x . x where � · � 0 simply counts the number of nonzero terms. However, such solution is generally NP-hard . Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Introduction Distributed Pattern Recognition Conclusion Seeking Sparsest Solution: ℓ 1 -Minimization Ideal solution: ℓ 0 -minimization 1 x ∗ = arg min y = ˜ ( P 0 ) � x � 0 s.t. ˜ A x . x where � · � 0 simply counts the number of nonzero terms. However, such solution is generally NP-hard . Compressed sensing : under mild condition, equivalence relation 2 x ∗ = arg min y = ˜ ( P 1 ) � x � 1 s.t. ˜ A x . x Allen Y. Yang Wearable Action Recognition <yang@eecs.berkeley.edu>
Recommend
More recommend