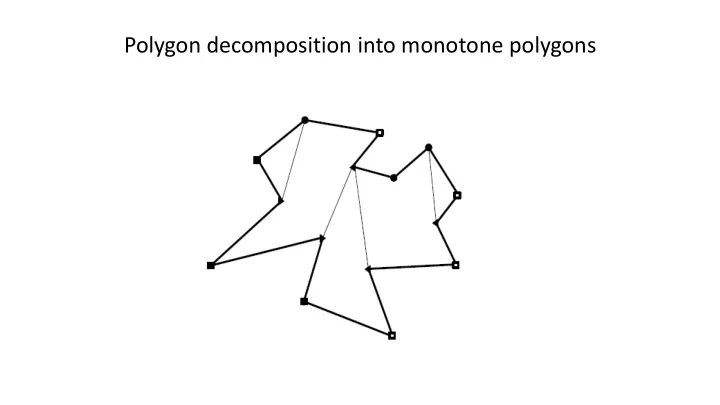
Polygon decomposition into monotone polygons Vertex types START - PowerPoint PPT Presentation

Polygon decomposition into monotone polygons

Vertex types START vertex (2 edges on the right and 𝛽 < 𝜌 ) END vertex (2 edges on the left and 𝛽 < 𝜌 ) SPLIT vertex (2 edges on the right and 𝛽 > 𝜌 ) MERGE vertex (2 edges on the left and 𝛽 > 𝜌 ) REGULAR vertex (1 edge on the left and 1 edge on the right)

Decomposition of polygon P into monotone polygons Global algorithm 1. Sort the vertices of P in a lexicographic order (i.e. first on x and then on y) and stock them in a priority queue Q 2. Initialize an empty binary tree T referred to as the status 3. while Q is not empty Remove the vertex 𝑤 𝑗 from Q Call the appropriate procedure to handle the vertex, depending on its type (see following slides)

Polygon decomposition into monotone polygons The algorithm proceeds like a planar left-to-right scan. Edges are added to and removed from the status T : For each edge 𝑓 𝑘 a corresponding vertex corr ( 𝑓 𝑘 ) exists. The corresponding vertices are defined by the algorithm itself while it scans the polygon. NB: The corresponding vertex of an edge can change during the algorithm execution!

START and END vertices handle_start_vertex( 𝑤 𝑗 ) { Insert 𝑓 𝑗 in T and set corr ( 𝑓 𝑗 ) to 𝑤 𝑗 } handle_end_vertex( 𝑤 𝑗 ) { if corr ( 𝑓 𝑗−1 ) is a MERGE vertex Insert the diagonal connecting 𝑤 𝑗 to corr ( 𝑓 𝑗−1 ) Delete 𝑓 𝑗−1 from T }

SPLIT and MERGE vertices handle_split_vertex( 𝑤 𝑗 ) { Search in T to find the edge 𝑓 𝑘 directly below 𝑤 𝑗 Insert the diagonal connecting 𝑤 𝑗 to corr ( 𝑓 𝑘 ) Set corr ( 𝑓 𝑘 ) to 𝑤 𝑗 Insert 𝑓 𝑗 in T and set corr ( 𝑓 𝑗 ) to 𝑤 𝑗 } handle_merge_vertex( 𝑤 𝑗 ) { if corr ( 𝑓 𝑗−1 ) is a MERGE vertex Insert the diagonal connecting 𝑤 𝑗 to corr ( 𝑓 𝑗−1 ) Delete 𝑓 𝑗−1 from T Search in T to find the edge 𝑓 𝑘 directly below 𝑤 𝑗 if corr ( 𝑓 𝑘 ) is a MERGE vertex Insert the diagonal connecting 𝑤 𝑗 to corr ( 𝑓 𝑘 ) Set corr ( 𝑓 𝑘 ) to 𝑤 𝑗 }

REGULAR vertices handle_regular_vertex( 𝑤 𝑗 ) { if the interior of P lies above vertex 𝑤 𝑗 if corr ( 𝑓 𝑗−1 ) is a MERGE vertex Insert the diagonal connecting 𝑤 𝑗 to corr ( 𝑓 𝑗−1 ) Delete 𝑓 𝑗−1 from T Insert 𝑓 𝑗 in T and set corr( 𝑓 𝑗 ) to 𝑤 𝑗 else Search in T to find the edge 𝑓 𝑘 directly below 𝑤 𝑗 if corr ( 𝑓 𝑘 ) is a MERGE vertex Insert the diagonal connecting 𝑤 𝑗 to corr ( 𝑓 𝑘 ) Set corr ( 𝑓 𝑘 ) to 𝑤 𝑗 }