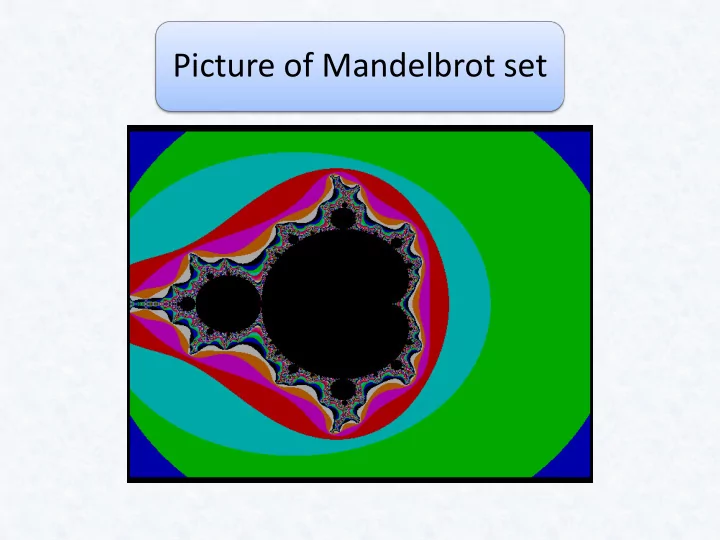
Picture of Mandelbrot set the Mandelbrot set has the property of - PowerPoint PPT Presentation

Picture of Mandelbrot set

the Mandelbrot set has the property of self-similarity. For example, if we zoom in on part of the Mandelbrot set, we will be able to find tiny replicas of the entire se t. See the illustration

Mandelbrot set has no shortage of copies of itself embedded into the image. Even parts of the Mandelbrot set that appear quite smooth and well-behaved in the original image s how a jagged outline consisting of lots and lots of tiny copies of the Mandelbrot set. For example, in the original image of the Mandelbrot set, there is a large, black region shaped like a cardioid, with a circle joined to it s upper right-hand corner. In the original image, the region where the cardioid and the circle are joined appears smooth. However, when the region is magnified, the detailed structure becomes apparent, and many, tiny copies of the Mandelbrot set can be seen

According the definition of the Mandelbrot set, this set consists of c - values for which the orbit with starting point zero does not escape when the function g(z) = z2 + c is used to do the iterations. One of the possible modifications or enhancements that you could have made to your program for drawing the Mandelbrot set was to include a feature that would draw Julia sets whe n specific points in the Mandelbrot set (i.e. c - values) were clicked on. The output from one version of such a program is given below. The diagram shows the Mandelbrot set along with the Julia sets corresponding to three of the points in the Mandelbrot set.

Parallel implementation 96*96 coordinate in the image Exploit these to calculate an entire row or column in parallel Each PE is allocated a row of the complete image. Each PE calculates the pixel value for its row simultaneously with column iterations Terminate() and calcres() modified to operate with poly variables

changes Use of poly array for rows of results. Get_penum() library function returns the PE number which allows the program to set up a unique y-coordinate for each of the Pes Dprint_poly_memory_raw() function prints out the values from the memory of each PE in turn.

Input and output Transfer data between mono and poly memory. Distribute data across the PE array for processing. Memcpy() library function Example program — uses library function to load array-sized chunks of data into PE memory from external (mono )memory

Limitations Does not overlap the i/o and compute operations. When data is read from mono memory using memcpym2p function, the PEs are idle while waiting for the data transfer to complete . Efficiency reduces when large number of PEs or large volume of data transfer to complete.

solution Supporting multithreading in the architecture. Allow – compute and i/o to be efficiently overlapped Use of asynchronous overlapped

Asynchronous I/O They execute on separate thread, allowing the compute thread to continue running. Id of a semaphore. Two buffers use  the active and background buffer

Modified program Read into the active buffer. Wait for the background buffer to be empty then read the next chunk into it. Wait for the active buffer to be full then process the contents. Write out the active buffer. Swap the active and background buffers. Repeat from 2 until all chunks are processed. Wait for the write of the last active buffer to finish then print the results to the console