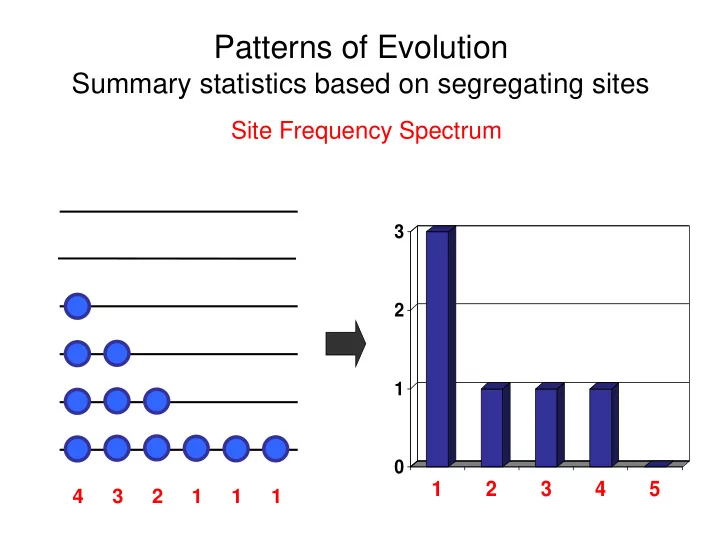
Patterns of Evolution Summary statistics based on segregating sites - PowerPoint PPT Presentation

Patterns of Evolution Summary statistics based on segregating sites Site Frequency Spectrum 3 2 1 0 1 2 3 4 5 4 3 2 1 1 1

Patterns of Evolution Summary statistics based on segregating sites Site Frequency Spectrum number of mutants : S that appear in i copies S i i in the sample 3  n 1 total number of   S S : segregating sites 2 i in an sample of size n  i 1  1 n 1 1 2     i ( n i ) S : i   n      i 1   0 average number of i 1 2 3 4 5 pairwise differences

Patterns of Evolution Summary statistics based on segregating sites Site Frequency Spectrum number of mutants : S that appear in i copies S i i in the sample 3  n 1 total number of   S S : segregating sites 2 i in an sample of size n  i 1  1 n 1 1 2     i ( n i ) S : i   n      i 1   Each mutation of size i 0 i 1 2 3 4 5 contributes to divergence in i ( n – i ) sequence pairs

Coalescent Theory Estimators Unbiased estimators of the mutation parameter q = 4 Nu :   n 1 n 1 S   1 ˆ q   Watterson‘s estimator: S (equal weights) W i a i   i 1 i 1 n   n 1 1 2  ˆ   (intermediate q       -based estimator:  n  ( ) i n i S   frequencies) i    i 1   n 1 1  ˆ   q  2  n  Fay and Wu‘s estimator: i S (high frequencies)   H i   2  i 1    n 1 ˆ q   singleton estimator: S S (extreme frequencies)  s 1 n 1 n singletons of the folded spectrum

Coalescent Theory Test statistics Test statistics for the deviation from neutrality : ˆ ˆ q  q   W D Tajima‘s D :   T  ˆ ˆ D 0 q  q Var T  W ˆ ˆ q  q 1  W S D Fu and Li‘s D :   FL 0,8 ˆ ˆ q  q Var 0,6 W S 0,4 0,2 ˆ ˆ q  q 0   H 1 2 3 4 5 6 H Fay and Wu‘s H :   FW ˆ ˆ q  q Var  H

Coalescent Theory Test statistics Test statistics for the deviation from neutrality : ˆ ˆ q  q   W D Tajima‘s D :   T  ˆ ˆ D 0 q  q Var T  W ˆ ˆ q  q 1  W S D Fu and Li‘s D :   FL 0,8 ˆ ˆ q  q Var 0,6 W S 0,4 0,2 ˆ ˆ q  q 0   H 1 2 3 4 5 6 H Fay and Wu‘s H :   FW ˆ ˆ q  q Var  H

Coalescent Theory Test statistics Test statistics for the deviation from neutrality : ˆ ˆ q  q   W D Tajima‘s D :   T  ˆ ˆ D 0 q  q Var FW  W ˆ ˆ q  q 1  W S D Fu and Li‘s D :   FL 0,8 ˆ ˆ q  q Var 0,6 W S 0,4 0,2 ˆ ˆ q  q 0   H 1 2 3 4 5 6 H Fay and Wu‘s H :   FW ˆ ˆ q  q Var  H

Coalescent Theory Test statistics Test statistics for the deviation from neutrality : ˆ ˆ q  q   W D Tajima‘s D :   T  ˆ ˆ H 0 q  q Var FW  W ˆ ˆ q  q 1  W S D Fu and Li‘s D :   FL 0,8 ˆ ˆ q  q Var 0,6 W S 0,4 0,2 ˆ ˆ q  q 0   H 1 2 3 4 5 6 H Fay and Wu‘s H :   FW ˆ ˆ q  q Var  H