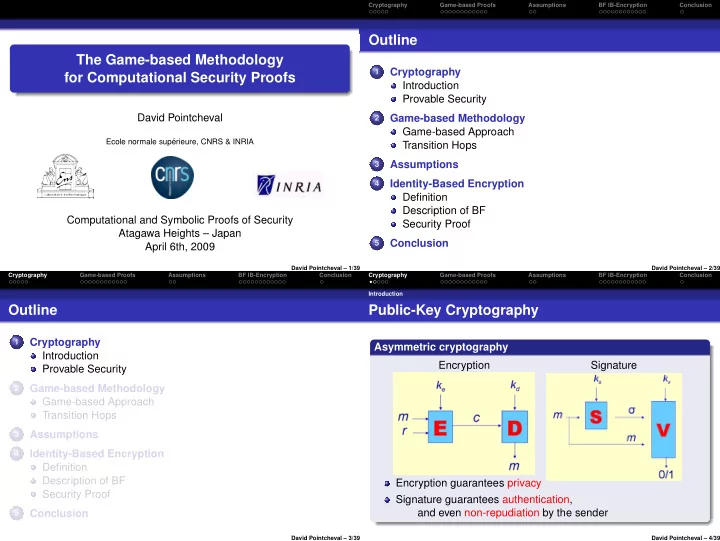

Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Outline The Game-based Methodology 1 Cryptography for Computational Security Proofs Introduction Provable Security David Pointcheval 2 Game-based Methodology Game-based Approach Ecole normale sup´ erieure, CNRS & INRIA Transition Hops Assumptions 3 4 Identity-Based Encryption Definition Description of BF Computational and Symbolic Proofs of Security Security Proof Atagawa Heights – Japan 5 Conclusion April 6th, 2009 David Pointcheval – 1/39 David Pointcheval – 2/39 Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Introduction Outline Public-Key Cryptography 1 Cryptography Asymmetric cryptography Introduction Encryption Signature Provable Security 2 Game-based Methodology Game-based Approach Transition Hops Assumptions 3 4 Identity-Based Encryption Definition Description of BF Encryption guarantees privacy Security Proof Signature guarantees authentication, 5 Conclusion and even non-repudiation by the sender David Pointcheval – 3/39 David Pointcheval – 4/39
Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Introduction Provable Security Strong Security Notions Provable Security One can prove that: Signature if an adversary is able to break the cryptographic scheme Existential Unforgeability under Chosen-Message Attacks then one can break the underlying problem An adversary, allowed to ask for signature on any message of its (integer factoring, discrete logarithm, 3-SAT, etc) choice, cannot generate a new valid message-signature pair Encryption Semantic Security against Chosen-Ciphertext Attacks An adversary that chooses 2 messages, and receives the encryption of one of them, is not able to guess which message has been encrypted, even if it is able to ask for decryption of any ciphertext of hard → its choice (except the challenge ciphertext) → solution instance David Pointcheval – 5/39 David Pointcheval – 6/39 Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Provable Security Provable Security Direct Reduction Game-based Methodology Illustration: OAEP [Bellare-Rogaway EC ’94] Reduction proven indistinguishable for an IND-CCA adversary (actually IND-CCA1, and not IND-CCA2) but widely believed for IND-CCA2, without any further analysis of the reduction The direct-reduction methodology [Shoup - Crypto ’01] Shoup showed the gap for IND-CCA2, under the OWP Unfortunately Granted his new game-based methodology [Fujisaki-Okamoto-Pointcheval-Stern – Crypto ’01] Security may rely on several assumptions FOPS proved the security for IND-CCA2, under the PD-OWP Proving that the view of the adversary, generated by the Using the game-based methodology simulator, in the reduction is the same as in the real attack game is not easy to do in such a one big step David Pointcheval – 7/39 David Pointcheval – 8/39
Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Game-based Approach Outline Sequence of Games 1 Cryptography Real Attack Game Introduction The adversary plays a game, against a challenger (security notion) Provable Security 2 Game-based Methodology Game-based Approach Transition Hops Assumptions 3 4 Identity-Based Encryption Definition Description of BF Security Proof 5 Conclusion David Pointcheval – 9/39 David Pointcheval – 10/39 Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Game-based Approach Game-based Approach Sequence of Games Sequence of Games Simulation Simulation The adversary plays a game, against a sequence of simulators The adversary plays a game, against a sequence of simulators David Pointcheval – 11/39 David Pointcheval – 12/39
Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Game-based Approach Game-based Approach Sequence of Games Output The output of the simulator in Game 1 is related to the output of Simulation the challenger in Game 0 (adversary’s winning probability) The adversary plays a game, against a sequence of simulators The output of the simulator in Game 3 is easy to evaluate (e.g. always zero, always 1, probability of one-half) The gaps (Game 1 ↔ Game 2, Game 2 ↔ Game 3, etc) are clearly identified with specific events David Pointcheval – 13/39 David Pointcheval – 14/39 Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Transition Hops Transition Hops Two Simulators Two Distributions perfectly identical behaviors perfectly identical input distributions [ Hop-S-Perfect ] [ Hop-D-Perfect ] different behaviors, only if event Ev happens different distributions Ev is negligible statistically close [ Hop-S-Negl ] [ Hop-D-Stat ] Ev is non-negligible computationally close [ Hop-S-Non-Negl ] [ Hop-D-Comp ] and independent of the output in Game A → Simulator B terminates in case of event Ev David Pointcheval – 15/39 David Pointcheval – 16/39
Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Transition Hops Transition Hops Two Simulations Two Simulations Identical behaviors: Pr [ Game A ] − Pr [ Game B ] = 0 Identical behaviors: Pr [ Game A ] − Pr [ Game B ] = 0 The behaviors differ only if Ev happens: The behaviors differ only if Ev happens: Ev is negligible, one can ignore it Ev is negligible, one can ignore it Shoup’s Lemma: Pr [ Game A ] − Pr [ Game B ] ≤ Pr [ Ev ] Ev is non-negligible and independent of the output in Game A , Simulator B terminates and outputs 0, in case of event Ev : | Pr [ Game A ] − Pr [ Game B ] | Pr [ Game B ] = Pr [ Game B | Ev ] Pr [ Ev ] + Pr [ Game B |¬ Ev ] Pr [ ¬ Ev ] � Pr [ Game A | Ev ] Pr [ Ev ] + Pr [ Game A |¬ Ev ] Pr [ ¬ Ev ] � = � � = 0 × Pr [ Ev ] + Pr [ Game A |¬ Ev ] × Pr [ ¬ Ev ] � − Pr [ Game B | Ev ] Pr [ Ev ] − Pr [ Game B |¬ Ev ] Pr [ ¬ Ev ] � � � = Pr [ Game A ] × Pr [ ¬ Ev ] � ( Pr [ Game A | Ev ] − Pr [ Game B | Ev ]) × Pr [ Ev ] � = � � � +( Pr [ Game A |¬ Ev ] − Pr [ Game B |¬ Ev ]) × Pr [ ¬ Ev ] � Simulator B terminates and flips a coin, in case of event Ev : � � ≤ | 1 × Pr [ Ev ] + 0 × Pr [ ¬ Ev ] | ≤ Pr [ Ev ] Pr [ Game B ] = Pr [ Game B | Ev ] Pr [ Ev ] + Pr [ Game B |¬ Ev ] Pr [ ¬ Ev ] = 1 2 × Pr [ Ev ] + Pr [ Game A |¬ Ev ] × Pr [ ¬ Ev ] Ev is non-negligible and independent of the output in Game A , = 1 2 + ( Pr [ Game A ] − 1 2 ) × Pr [ ¬ Ev ] Simulator B terminates in case of event Ev David Pointcheval – 17/39 David Pointcheval – 18/39 Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Cryptography Game-based Proofs Assumptions BF IB-Encryption Conclusion Transition Hops Transition Hops Two Simulations Two Distributions Identical behaviors: Pr [ Game A ] − Pr [ Game B ] = 0 The behaviors differ only if Ev happens: Ev is negligible, one can ignore it Ev is non-negligible and independent of the output in Game A , Simulator B terminates in case of event Ev Event Ev Either Ev is negligible, or the output is independent of Ev For being able to terminate simulation B in case of event Ev , this event must be efficiently detectable For evaluating Pr [ Ev ] , one re-iterates the above process, Pr [ Game A ] − Pr [ Game B ] ≤ Adv ( D oracles ) with an initial game that outputs 1 when event Ev happens David Pointcheval – 19/39 David Pointcheval – 20/39
Recommend
More recommend