Nuclear Chart Periodic Table of the Elements Group** Period 1 18 - PDF document

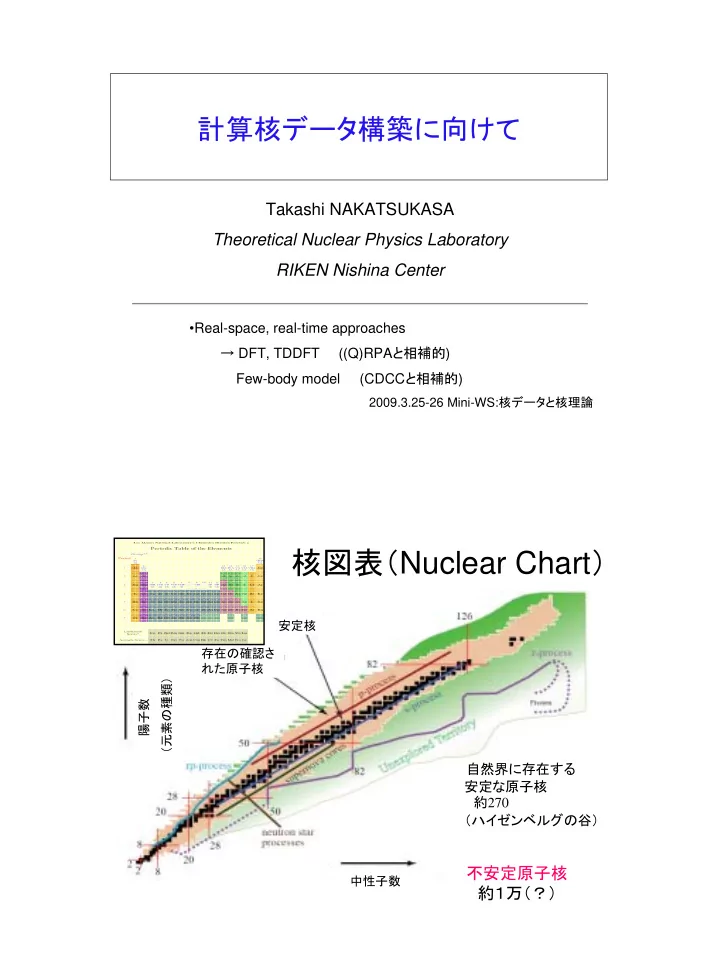
計算核データ 構築に向けて Takashi NAKATSUKASA Theoretical Nuclear Physics Laboratory RIKEN Nishina Center •Real-space, real-time approaches → DFT, TDDFT ((Q)RPA と 相補的 ) Few-body model (CDCC と 相補的 ) 2009.3.25-26 Mini-WS: 核データ と 核理論 Los Alamos National Laboratory's Chemistry Division Presents a 核図表（ Nuclear Chart ） Periodic Table of the Elements Group** Period 1 18 IA V IIIA 1A 8A 1 2 2 13 14 15 16 17 1 H IIA IIIA IVA VA VIA VIIA He 1.008 2A 3A 4A 5A 6A 7A 4.003 3 4 5 6 7 8 9 10 2 Li Be B C N O F Ne 6.941 9.012 10.81 12.01 14.01 16.00 19.00 20.18 11 12 8 9 10 13 14 15 16 17 18 3 4 5 6 7 11 12 3 Na Mg IIIB IVB VB VIB VIIB ------- VIII ----- IB IIB Al Si P S Cl Ar 22.99 24.31 3B 4B 5B 6B 7B -- 1B 2B 26.98 28.09 30.97 32.07 35.45 39.95 ------- 8 ------- 20 21 22 23 24 25 28 29 30 31 32 34 35 36 19 26 27 33 4 K Ca Sc Ti V Cr Mn Fe Co Ni Cu Zn Ga Ge As Se Br Kr 39.10 40.08 44.96 47.88 50.94 52.00 54.94 55.85 58.47 58.69 63.55 65.39 69.72 72.59 74.92 78.96 79.90 83.80 37 38 39 40 41 42 43 46 47 48 49 50 51 52 53 54 44 45 5 Rb Sr Y Zr Nb Mo Tc Ru Rh Pd Ag Cd In Sn Sb Te I Xe 85.47 87.62 88.91 91.22 92.91 95.94 (98) 106.4 107.9 112.4 114.8 118.7 121.8 127.6 126.9 131.3 101.1 102.9 55 56 57 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 6 Cs Ba La* Hf Ta W Re Os Ir Pt Au Hg Tl Pb Bi Po At Rn 132.9 137.3 138.9 178.5 180.9 183.9 186.2 190.2 190.2 195.1 197.0 200.5 204.4 207.2 209.0 (210) (210) (222) 87 88 89 104 105 106 107 108 109 110 111 112 114 116 118 7 Fr Ra Ac~ Rf Db Sg Bh Hs Mt --- --- --- --- --- --- (223) (226) (227) (257) (260) (263) (262) (265) (266) () () () () () () 安定核 58 59 60 61 62 65 66 67 68 69 70 71 Lanthanide 63 64 Ce Pr Nd Pm Sm Eu Gd Tb Dy Ho Er Tm Yb Lu Series* 140.1 140.9 144.2 (147) 150.4 158.9 162.5 164.9 167.3 168.9 173.0 175.0 152.0 157.3 90 91 92 93 94 97 98 99 100 101 102 103 95 96 Actinide Series~ Th Pa U Np Pu Am Cm Bk Cf Es Fm Md No Lr 232.0 (231) (238) (237) (242) (243) (247) (247) (249) (254) (253) (256) (254) (257) 存在の確認さ れた原子核 元素の種類） 陽子数 （ 自然界に存在する 安定な原子核 約 270 （ ハイ ゼンベルグの谷） 不安定原子核 中性子数 約１ 万（ ？）

High-performance computing ~ DFT to cover all One-to-one Correspondence Density Minimum-energy state External potential r ( ) ρ Ψ r Ground state v -representative density r ( ) V r Ψ ρ r ( r ) V V

The following variation leads to all the ground-state properties. { ( ) } 0 r r r r r [ ] ∫ ∫ δ ρ + ρ − µ ρ − = F ( r ) v ( r ) d r ( r ) d r N In principle, any physical quantity of the ground state should be a functional of density. r r Ψ L ( 1 r , , r ) Variation with respect to many-body wave functions N ↓ r ρ ( r ) Variation with respect to one-body density ↓ r ρ = Ψ ρ Ψ ρ ˆ Physical quantity A [ ( r )] [ ] A [ ] Kohn-Sham Scheme Real interacting system density Ground state V r r ( r ) ( ) ρ Ψ r V Virtual non-interacting system density r Ground state V s ( r ) Ψ r ( ) ρ S r

Kohn-Sham scheme { ( ) } r r r ( ) ( ) = ∑ ρ φ 2 Ψ = φ r r det r i i j S i 2 h [ ] − ∇ φ + ρ φ = ε φ 2 v KS canonical equation i S i i i 2 m Density functional r [ ] ( ) r r r r [ ( ) ] [ ( ) ] ( [ ( ) ] [ ( ) ] ) ρ ρ = ρ + ρ − ρ V r F r T r F r T r eff S S r 2 r p [ ( ) ] ∑ = φ φ + ρ V r i i eff 2 m i Minimization of this density functional leads to δ [ ] ( ) r V ρ = eff v S r r ( ) δρ r Nuclear DFT Global properties, global calculat ions S. Goriely et al., ENAM’04 M. Stoitsov et al. * Global DFT mass calculations: HFB mass formula: ∆ m~700keV • Taking advantage of high-performance computers

One-to-one Correspondence Time-dependent state starting from the initial state Time-dependent External potential Ψ ( 0 t ) density TD state v -representative density r ( ) V r Ψ ρ ( t ) r , t ( r , t ) V ( t ) V TD Kohn-Sham Scheme Real interacting system TD state TD density V r r ( r , t ) ( ) ρ r , t Ψ ( t ) V Virtual non-interacting system TD state TD density r V s ( r , t ) Ψ ( t ) r ( ) ρ S r , t

Skyrme TDDFT in real space ( ) ~ − i η Time-dependent Kohn-Sham equation r ( ) ∂ t ψ στ = ρ τ + ψ στ i ( r , t ) h [ , , j , s , J ]( t ) V ( t ) ( r , t ) ∂ i HF ex t i t 3D space is discretized in lattice ϕ = ϕ = = L n 1 , Mt L Single-particle orbital: ( r , t ) { ( r , t )} , i 1 , , N = i i k n k 1 , L Mr N: Number of particles Mr : Number of mesh points y [ fm ] Mt : Number of time slices Spatial mesh size is about 1 fm. Time step is about 0.2 fm/c Nakatsukasa, Yabana, Phys. Rev. C71 (2005) 024301 X [ fm ] Real-time calculation of response functions Ψ Ψ ˆ ( t ) F ( t ) 1. Weak instantaneous external perturbation = δ ˆ V ( t ) F ( t ) ext 2. Calculate time evolution of 0 1 2 3 Ψ ˆ Ψ ( t ) F ( t ) t [ /MeV ] ω 3. Fourier transform to energy domain ˆ dB ( ; F ) ω ˆ ω dB ( ; F ) 1 d ∫ i ω = − Ψ ˆ Ψ t Im ( t ) F ( t ) e dt ω π d ω [ MeV ]

Neutrons 16 O ( ) n δρ = ρ − ρ ( t ) ( t ) n n 0 Time-dep. transition density δρ > 0 δρ < 0 ( ) p δρ = ρ − ρ ( t ) ( t ) p p 0 Protons 18 O 16 O Prolate 10 30 20 40 E x [ MeV ]

26 Mg 24 Mg Triaxial Prolate 10 20 30 40 10 20 30 40 E x [ MeV ] E x [ MeV ] 28 Si 30 Si Oblate Oblate 10 20 30 40 E x [ MeV ] 10 20 30 40 E x [ MeV ]

40 Ar Oblate 40 20 30 10 E x [ MeV ] 44 Ca Prolate 48 Ca 40 Ca 10 20 30 E x [ MeV ] 10 20 30 40 E x [ MeV ] 10 20 30 40 E x [ MeV ]

Cal. vs. Exp. Electric dipole strengths Z SkM* R box = 15 fm Γ = 1 MeV Numerical calculations by T.Inakura (Univ. of Tsukuba) N

Few-body-model calculation of fusion cross section • Real-time, real-space approach • No need for scattering boundary condition • Alternative method to the CDCC Wave packet dynamics of fusion reaction potential scattering with absorption inside a Coulomb barrier Radial Schroedinger equation for l=0 ∂   h 2 2 ( ) ( ) ( ) ( ) d = − + + h   i u r , t V r iW r u r , t ∂ 2   t 2 m dr with incident Gaussian wave packet [ ] ( ) ( ) 10Be-208Pb (A,Z=10,4 and 208,82) = − − γ − 2 u r , t exp ikr r r V0=-50 W0=-10, RV=1.26,RW=1.215, AV=0.44, AW=0.45 0 0 E_inc=28 MeV (+Coulomb at R_0), R_0=40fm, gamma=0.1fm-2 Nr=400, dr=0.25, Nt=10000, dt=0.001 ( ) V r 10 Be – 208 Pb ( ) W r Flux absorbed by W(r) represents fusion. Wave packet dynamics include scattering information for wide energy region. Then, how to extract reaction information for a fixed energy?

Fusion probability ( ) ( ) − P E P E = init final P ( E ) ( ) fusion P E differential. eq. (static cal) init wave packet method - 3 1 0 0 x 1 0 1 . 0 n 8 0 F u s i o n p r o b . ( t i m e - d e p . ) o i t F u s i o n p r o b . ( s t a t i c ) u b 6 0 i r t s 0 . 8 i d 4 0 y g r e n E 2 0 0 . 6 0 0 1 0 2 0 3 0 4 0 5 0 6 0 0 . 4 E n e r g y [ M e V ] 0 . 2 0 . 0 2 5 3 0 3 5 4 0 4 5 5 0 E n e r g y [ M e V ] Fusion probability for whole barrier region from single wave-packet calculation. No boundary condition required in the wave packet calculation. Fusion probability of three-body reaction ( ) ( )   ∂ h 2 h 2 ( ) ( ) ( )   ψ = − ∇ − ∇ + + + ψ 2 2 h i R , r , t V r V r V r R , r , t   ∂ µ R r nC nC CT CT nT nT   t 2 2 m Coulomb + Nuclear potential ( ) ( ) ( J Absorption => C-T fusion ∑ u R , r , t ) ψ = θ l R , r , t P cos J l Rr l Initial incident wave Transfer Elastic Flux loss by absorption Breakup → FUSION (Complete + Incomplete)

n ( ) ( ) r − P E P E ( ) r = θ i f P E ( ) fusion P E C i 1 . 0 R T 2 - b o d y t r a n s f e r m a t c h i n g 0 . 8 y t i l i 0 . 6 b a b o r p n o 0 . 4 (nC)-T 3-body i s u F 0 . 2 C-T 2-body 0 . 0 8 9 1 0 1 1 1 2 1 3 1 4 1 5 E n e r g y [ M e V ] Enhancement of fusion probability at sub-barrier energies Case (2): Weakly-bound projectile ( Neutron-halo ) y ・ n-C orbital energy: -0.6 MeV (Halo) neutron r x θ r 11 Be(n+ 10 Be)- 208 Pb R Target Core head-on collision (J=0) ( ) ( ) ( ) ( ) ( ) ∫ ∫ ρ = θ ψ θ 2 ρ θ = ψ θ 2 R , r , t d cos R , r , , t r , , t dR R , r , , t y R x r