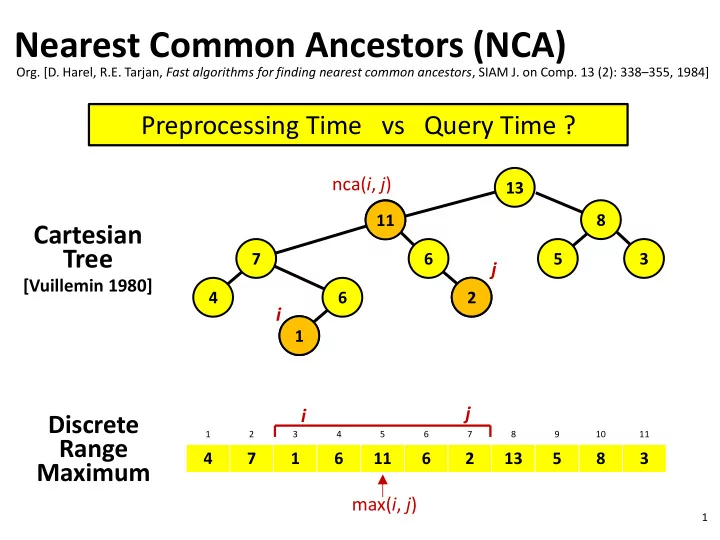
Nearest Common Ancestors (NCA) Org. [D. Harel, R.E. Tarjan, Fast - PowerPoint PPT Presentation

Nearest Common Ancestors (NCA) Org. [D. Harel, R.E. Tarjan, Fast algorithms for finding nearest common ancestors , SIAM J. on Comp. 13 (2): 338 – 355, 1984] Preprocessing Time vs Query Time ? nca( i , j ) 13 11 8 11 Cartesian Tree 7 6 5 3 j [Vuillemin 1980] 4 6 2 2 i 1 1 j i Discrete 1 2 3 4 5 6 7 8 9 10 11 Range 4 7 1 6 11 6 2 13 5 8 3 Maximum max( i , j ) 1

Cartesian Tree Construction  Incremental construction left-to-right 18 18 13 + 13 10 10 8 START 8 2 HERE 2 18 ∙∙∙ 13 ∙∙∙ 8 ∙∙∙ 2 10  O( n ) time ( Φ = #nodes on rightmost path) 2

Reduction: NCA   1 Discrete Range Maximum nca( i , j ) Euler Tour H E E J B F I K A D G G j i C C nca( i , j ) j i node H E B A B D C D B E F G F E H J I J K J H depth 1 2 3 4 3 4 5 4 3 2 2 3 4 3 2 1 2 3 2 3 2 1 minimum depth 3

NCA on Perfect Binary Trees 1 2 3 4 5 = nca(11,21) i 11 2 i 2 i +1 10 20 21 22 23 11 = 1011 2 longest common prefix 21 = 10101 2 nca(21,21) = 5 = 101 2 = lcp( 101 1 2 , 101 01 2 ) proc lcp( x , y ) position of most significant bit ≠ 0 if y < x then swap ( x , y ) return x >> (msb( x XOR ( y >> (msb( y )-msb( x ))) 4

Discrete Range Mimimum – Space O( n ∙log n ) words nca( i , j ) 1 1 1 1 3 2 1 1 3 3 4 2 3 2 1 1 2 3 4 3 4 5 4 3 2 3 4 3 2 1 2 0 1 i ∙ ∙ ∙ j 1 2 3 4 3 4 5 4 3 2 3 4 3 2 1 2 3 3 1 3 3 2 3 3 3 d 3 2 1 1 5 right i left j drm( i , j ) = min(right i ( d ), left j ( d )) d = msb( i XOR j ) 5

Blocked solution – Space O( n ) words Top structure O( n /log n ) elements Space O( n ) Query O(1) 1 2 1 2 1 2 3 4 3 4 5 4 1 4 3 4 3 2 3 2 j i block of O(log n ) elements W j (One for each j ) 0 1 0 1 1 5 4 3 2 1 Block query: j +1-msb( W j AND ((1 << ( j - i +1))-1)) General query: 1 top query + 2 bottom queries O( n ) Preprocessing Time O(1) Query Time 6

Summary... General Discrete Range Searching j i 1 2 3 4 5 6 7 8 4 7 1 6 8 6 2 9 Cartesian Tree nca( i , j ) 9 8 7 6 NCA j 4 6 2 1 i Discrete Range Max on Depth Array 1 2 3 4 3 4 5 4 3 2 3 4 3 2 1 ”O( n ∙log n )” solution on O( n /log n ) blocks O(log n ) size blocks O( n ) Preprocessing Time O(1) Query Time 7

1d & 2D DRM Results Indexing Model Encoding Model (input accessible) (input not accessable) 2 n + o ( n ) bits, O (1) time [FH07] m = 1 ≥ 2 n - O (log n ) bits n / c bits  Ω( c ) time [BDR10] 2 n + o ( n ) bits, O (1) time [F10] 1D n / c bits, O (c) time [BDR10] Ω( mn  log m ) bits [BDR10] 1 < m < n O ( mn  log n ) bits, O (1) time [AY10] O ( mn  log n ) bits, O (1) time [BDR10] O ( mn ) bits, O (1) time [BDR10] O ( mn  log m ) bits, O ( mn ) time [BBD13] mn / c bits  Ω( c ) time [BDR10] O ( c  log 2 c ) time [BDR10] Ω( mn  log n ) bits [DLW09] m = n O ( c  log c  (loglog c ) 2 ) time [BDLRR12] O ( mn  log n ) bits, O (1) time [AY10] squared better upper or lower bound ?

DRM encoding - O( n ) bits j i A B C D E F G H I J K 1 2 3 4 5 6 7 8 9 10 11 nca( i , j ) 4 7 1 6 11 6 2 13 5 8 3 Euler Tour H Cartesian E E J Tree B F I K A D G G j i C C nca( i , j ) node H E B A B D C D B E F G F E H J I J K J H depth 1 2 3 4 3 4 5 4 3 2 2 3 4 3 2 1 2 3 2 3 2 1 minimum depth select( i ) = i ’th ”1” p i j ’th ”1” = select( j ) p p j 0 0 0 1 1 0 1 1 0 1 1 1 0 0 1 0 1 1 1 0 0 4 n bits + + + + - + + - - - + + - - - + + - + - - rank( p ) = drm( i , j ) = # 1 left of p depth = # + - # - = min-prefix-sum( p i , p j ) 9

Succinct data structures for DRM, O( n ) bits α = ½  log n bits i ’th ”1” = select( i ) p  1 0 0 0 0 1 1 0 1 1 0 1 1 1 0 0 1 0 1 1 1 0 0 … B 0 B 1 B 2 B 3 R 1 [ i ] = # 1 in first i blocks ( n / α  log n bits) rank( p ) = R 1 [ └ p / α ┘ ] + T rank [B[ └ p / α ┘ ], p mod α ] T rank = rank inside block, table lookup (2 α +log α  log α bits) α +log α bits i is in block B[ b ] select( i ) = α b + T select [B[ b ], i -rank( α b -1)] leader[ i ] = is the i th ”1” the first ”1” in its block? ( n bits) b = R nonempty [rank leader ( i )] rank leader ( i ) = rank structure for leader array (O( n ) bits) R nonempty = index of nonempty blocks ( n / α  log n bits) T select = select inside block, table lookup (2 α +log α  log α bits) min-prefix-sum( p i , p j ) = α ( b k -1)+ d k PS[ b ] = # + - # - for blocks B 0 .. B b ( n / α  log n bits) b 1 = └ p i / α ┘ T ps = # + - # - for block prefix, b 3 = └ p j / α ┘ table lookup (2 α +log α  (1+log α ) bits) b 2 = drm PS ( b 1 +1, b 3 -1) T mps = index of minimum prefix sum # + - # - inside range in a block, table lookup (2 α +2log α  log α bits) d 1 = T mps [B[ b 1 ], p i mod α , α -1] MPS[ b ] = PS[ b -1]+ T mps [B[ b ], 0, α -1] ( n / α  log n bits) d 2 = T mps [B[ b 2 ], 0, α -1] drm MPS = drmin structure for MPS, O( n / α ) words (O( n ) bits) d 3 = T mps [B[ b 3 ], 0, p j mod α ] b 1 b 2 b 3 MPS 1 3 2 1 2 1 k = argmin t =1..3 PS[ b t -1]+T ps [B[ b t ], d t ] d 3 =1 d 1 =3 p j p i d 2 =2 + + + + - + + - - - + + - - - + + - + - - 10 B b 1 B b 2 B b 3