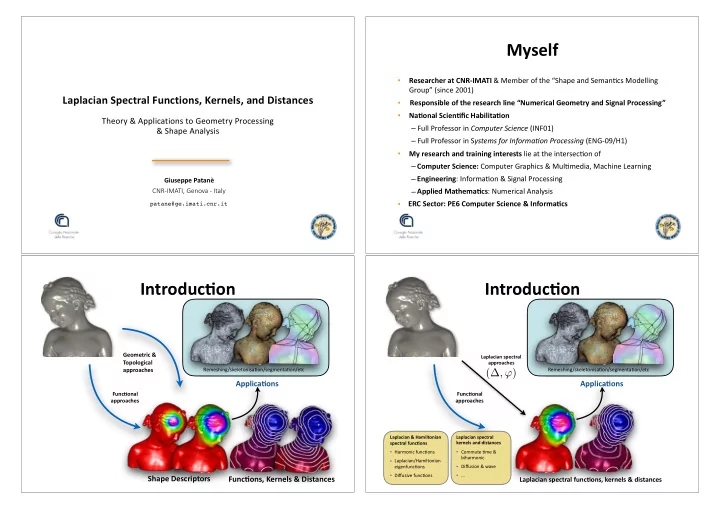
myself
play

Myself Researcher at CNR-IMATI & Member of the Shape and - PowerPoint PPT Presentation

Dec 12, 2023 •369 likes •662 views

Myself Researcher at CNR-IMATI & Member of the Shape and Seman<cs Modelling Group (since 2001) Laplacian Spectral Functions, Kernels, and Distances Responsible of the research line Numerical Geometry and Signal

  1. Myself • Researcher at CNR-IMATI & Member of the “Shape and Seman<cs Modelling Group” (since 2001) Laplacian Spectral Functions, Kernels, and Distances • Responsible of the research line “Numerical Geometry and Signal Processing” • NaHonal ScienHfic HabilitaHon Theory & Applications to Geometry Processing – Full Professor in Computer Science (INF01) & Shape Analysis – Full Professor in S ystems for Informa3on Processing (ENG-09/H1) My research and training interests lie at the intersec<on of • – Computer Science: Computer Graphics & Mul<media, Machine Learning – Engineering : Informa<on & Signal Processing Giuseppe Patanè – Applied MathemaHcs : Numerical Analysis CNR-IMATI, Genova - Italy ERC Sector: PE6 Computer Science & InformaHcs • patane@ge.imati.cnr.it IntroducHon IntroducHon Geometric & Laplacian spectral Topological approaches approaches Remeshing/skeletonisa<on/segmenta<on/etc Remeshing/skeletonisa<on/segmenta<on/etc ( ∆ , ϕ ) ApplicaHons ApplicaHons FuncHonal FuncHonal approaches approaches Laplacian & Hamiltonian Laplacian spectral kernels and distances spectral funcHons • Harmonic func<ons • Commute <me & biharmonic • Laplacian/Hamiltonian • Diffusion & wave eigenfunc<ons • … • Diffusive func<ons Shape Descriptors FuncHons, Kernels & Distances Laplacian spectral funcHons, kernels & distances

  2. <latexit sha1_base64="meX57DK1w2i7CaTi1VTDOai/VSY=">AB8HicbVBNS8NAFHzxs9avqkcvi0XwVBIR1FvRi8cKxhbUjbTbt0s4m7L0IJ/RdePKh49ed489+4aXPQ1oGFYeY9dt4EiRQGXfbWVpeWV1bL2UN7e2d3Yre/v3Jk414z6LZaxbATVcCsV9FCh5K9GcRoHkzWB0nfvNJ6NiNUdjhPejehAiVAwilZ6EQUh0GYPU56lapbc6cgi8QrSBUKNHqVr04/ZmnEFTJjWl7boLdjGoUTPJuZManlA2ogPetlTRiJtuNk08IcdW6ZMw1vYpJFP190ZGI2PGUWAn84Rm3svF/7x2iuFNxMqSZErNvsoTCXBmOTnk7QnKEcW0KZFjYrYUOqKUNbUtmW4M2fvEj809plzbs9q9avijZKcAhHcAIenEMdbqABPjBQ8Ayv8OY58V5dz5mo0tOsXMAf+B8/gBdNJDp</latexit> <latexit sha1_base64="meX57DK1w2i7CaTi1VTDOai/VSY=">AB8HicbVBNS8NAFHzxs9avqkcvi0XwVBIR1FvRi8cKxhbUjbTbt0s4m7L0IJ/RdePKh49ed489+4aXPQ1oGFYeY9dt4EiRQGXfbWVpeWV1bL2UN7e2d3Yre/v3Jk414z6LZaxbATVcCsV9FCh5K9GcRoHkzWB0nfvNJ6NiNUdjhPejehAiVAwilZ6EQUh0GYPU56lapbc6cgi8QrSBUKNHqVr04/ZmnEFTJjWl7boLdjGoUTPJuZManlA2ogPetlTRiJtuNk08IcdW6ZMw1vYpJFP190ZGI2PGUWAn84Rm3svF/7x2iuFNxMqSZErNvsoTCXBmOTnk7QnKEcW0KZFjYrYUOqKUNbUtmW4M2fvEj809plzbs9q9avijZKcAhHcAIenEMdbqABPjBQ8Ayv8OY58V5dz5mo0tOsXMAf+B8/gBdNJDp</latexit> <latexit sha1_base64="meX57DK1w2i7CaTi1VTDOai/VSY=">AB8HicbVBNS8NAFHzxs9avqkcvi0XwVBIR1FvRi8cKxhbUjbTbt0s4m7L0IJ/RdePKh49ed489+4aXPQ1oGFYeY9dt4EiRQGXfbWVpeWV1bL2UN7e2d3Yre/v3Jk414z6LZaxbATVcCsV9FCh5K9GcRoHkzWB0nfvNJ6NiNUdjhPejehAiVAwilZ6EQUh0GYPU56lapbc6cgi8QrSBUKNHqVr04/ZmnEFTJjWl7boLdjGoUTPJuZManlA2ogPetlTRiJtuNk08IcdW6ZMw1vYpJFP190ZGI2PGUWAn84Rm3svF/7x2iuFNxMqSZErNvsoTCXBmOTnk7QnKEcW0KZFjYrYUOqKUNbUtmW4M2fvEj809plzbs9q9avijZKcAhHcAIenEMdbqABPjBQ8Ayv8OY58V5dz5mo0tOsXMAf+B8/gBdNJDp</latexit> <latexit sha1_base64="meX57DK1w2i7CaTi1VTDOai/VSY=">AB8HicbVBNS8NAFHzxs9avqkcvi0XwVBIR1FvRi8cKxhbUjbTbt0s4m7L0IJ/RdePKh49ed489+4aXPQ1oGFYeY9dt4EiRQGXfbWVpeWV1bL2UN7e2d3Yre/v3Jk414z6LZaxbATVcCsV9FCh5K9GcRoHkzWB0nfvNJ6NiNUdjhPejehAiVAwilZ6EQUh0GYPU56lapbc6cgi8QrSBUKNHqVr04/ZmnEFTJjWl7boLdjGoUTPJuZManlA2ogPetlTRiJtuNk08IcdW6ZMw1vYpJFP190ZGI2PGUWAn84Rm3svF/7x2iuFNxMqSZErNvsoTCXBmOTnk7QnKEcW0KZFjYrYUOqKUNbUtmW4M2fvEj809plzbs9q9avijZKcAhHcAIenEMdbqABPjBQ8Ayv8OY58V5dz5mo0tOsXMAf+B8/gBdNJDp</latexit> <latexit sha1_base64="TxjeQN1S0yLSUh93TOGy+Iti9rM=">AB8HicbVBNS8NAFHypX7V+VT16WSyCp5KIoN6KXjxWMLbYlrLZvrRLN5uwuxFK6L/w4kHFqz/Hm/GTZuDtg4sDPvsfMmSATXxnW/ndLK6tr6RnmzsrW9s7tX3T940HGqGPosFrFqB1Sj4BJ9w43AdqKQRoHAVjC+yf3WEyrNY3lvJgn2IjqUPOSMGis9diNqRkGYJdN+tebW3RnIMvEKUoMCzX71qzuIWRqhNExQrTuem5heRpXhTOC0k01JpSN6RA7lkoaoe5ls8RTcmKVAQljZ80ZKb+3shopPUkCuxknlAvern4n9dJTXjZy7hMUoOSzT8KU0FMTPLzyYArZEZMLKFMcZuVsBFVlBlbUsW4C2evEz8s/pV3bs7rzWuizbKcATHcAoeXEADbqEJPjCQ8Ayv8OZo58V5dz7moyWn2DmEP3A+fwBbsJDo</latexit> <latexit sha1_base64="TxjeQN1S0yLSUh93TOGy+Iti9rM=">AB8HicbVBNS8NAFHypX7V+VT16WSyCp5KIoN6KXjxWMLbYlrLZvrRLN5uwuxFK6L/w4kHFqz/Hm/GTZuDtg4sDPvsfMmSATXxnW/ndLK6tr6RnmzsrW9s7tX3T940HGqGPosFrFqB1Sj4BJ9w43AdqKQRoHAVjC+yf3WEyrNY3lvJgn2IjqUPOSMGis9diNqRkGYJdN+tebW3RnIMvEKUoMCzX71qzuIWRqhNExQrTuem5heRpXhTOC0k01JpSN6RA7lkoaoe5ls8RTcmKVAQljZ80ZKb+3shopPUkCuxknlAvern4n9dJTXjZy7hMUoOSzT8KU0FMTPLzyYArZEZMLKFMcZuVsBFVlBlbUsW4C2evEz8s/pV3bs7rzWuizbKcATHcAoeXEADbqEJPjCQ8Ayv8OZo58V5dz7moyWn2DmEP3A+fwBbsJDo</latexit> <latexit sha1_base64="TxjeQN1S0yLSUh93TOGy+Iti9rM=">AB8HicbVBNS8NAFHypX7V+VT16WSyCp5KIoN6KXjxWMLbYlrLZvrRLN5uwuxFK6L/w4kHFqz/Hm/GTZuDtg4sDPvsfMmSATXxnW/ndLK6tr6RnmzsrW9s7tX3T940HGqGPosFrFqB1Sj4BJ9w43AdqKQRoHAVjC+yf3WEyrNY3lvJgn2IjqUPOSMGis9diNqRkGYJdN+tebW3RnIMvEKUoMCzX71qzuIWRqhNExQrTuem5heRpXhTOC0k01JpSN6RA7lkoaoe5ls8RTcmKVAQljZ80ZKb+3shopPUkCuxknlAvern4n9dJTXjZy7hMUoOSzT8KU0FMTPLzyYArZEZMLKFMcZuVsBFVlBlbUsW4C2evEz8s/pV3bs7rzWuizbKcATHcAoeXEADbqEJPjCQ8Ayv8OZo58V5dz7moyWn2DmEP3A+fwBbsJDo</latexit> <latexit sha1_base64="TxjeQN1S0yLSUh93TOGy+Iti9rM=">AB8HicbVBNS8NAFHypX7V+VT16WSyCp5KIoN6KXjxWMLbYlrLZvrRLN5uwuxFK6L/w4kHFqz/Hm/GTZuDtg4sDPvsfMmSATXxnW/ndLK6tr6RnmzsrW9s7tX3T940HGqGPosFrFqB1Sj4BJ9w43AdqKQRoHAVjC+yf3WEyrNY3lvJgn2IjqUPOSMGis9diNqRkGYJdN+tebW3RnIMvEKUoMCzX71qzuIWRqhNExQrTuem5heRpXhTOC0k01JpSN6RA7lkoaoe5ls8RTcmKVAQljZ80ZKb+3shopPUkCuxknlAvern4n9dJTXjZy7hMUoOSzT8KU0FMTPLzyYArZEZMLKFMcZuVsBFVlBlbUsW4C2evEz8s/pV3bs7rzWuizbKcATHcAoeXEADbqEJPjCQ8Ayv8OZo58V5dz7moyWn2DmEP3A+fwBbsJDo</latexit> IntroducHon IntroducHon • Working on the space of scalar funcHons defined on the input domain (eg., surface, • Target properHes of the Laplacian spectral volume), we can address Different resoluHons func<ons, kernels, and distances – mulH-scale signal representaHons and denoising , by projec<ng the input – smoothness & orthonormality signals/data on a set of ( mul3-scale ) basis func<ons – intrinsic definiHon ; ie., independent of data – sparse representaHons , by choosing a low number of basis func<ons in order to embedding/representa<on achieve a target approxima<on accuracy Different postures – mulH-scale definiHon , in order to encode – compression , by quan<sing the representa<on coefficients local and global shape features k – invariance to shape transformaHons ; eg., X f = α i ϕ i isometries for pose invariance i =1 – compact support & localisaHon at feature/ f = ( x, y, z ) k = 3 , 20 , 50 , . . . Different & parHal representaHons seed points for encoding local geometry MulH-scale/sparse proper<es & saving memory space representaHon – efficient, stable, and parameter-free computaHon Compression IntroducHon IntroducHon Working on the space of scalar funcHons defined on the input domain (eg., surface, Working on the space of scalar funcHons defined on the input domain (eg., surface, • • volume), we can address volume), we can address – shape deformaHons , by modifying the coefficients that express the geometry of – the defini<on of Laplacian spectral kernels and distances , as a filtered the input surface in terms of geometry-driven or shape-intrinsic basis funcHons combina<on of the Laplacian spectral basis (eg., harmonic barycentric coordinates) X f = α i ( t ) ϕ i i q seed point p X d 2 ( p , q ) := α i | ϕ i ( p ) − ϕ i ( q ) | 2 Global basis Local basis i

Recommend

More recommend