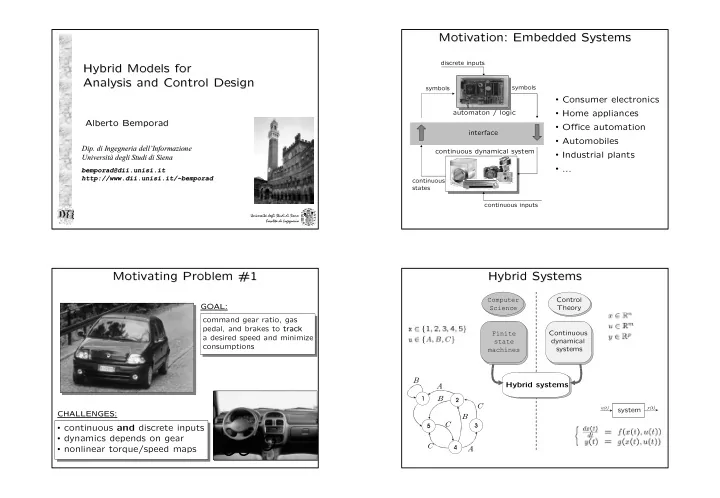

Motivation: Embedded Systems Motivation: Embedded Systems discrete inputs Hybrid Models for Hybrid Models for Analysis and Control Design Analysis and Control Design symbols symbols • Consumer electronics • Home appliances automaton / logic Alberto Bemporad Alberto Bemporad • Office automation interface • Automobiles Dip. di Dip. di Ingegneria Ingegneria dell’Informazione dell’Informazione continuous dynamical system • Industrial plants Università degli degli Studi Studi di Siena di Siena Università • ... bemporad@dii.unisi.it bemporad@dii.unisi.it http://www.dii.unisi.it/~bemporad http:// www.dii.unisi.it/~bemporad continuous states continuous inputs Università degli Studi di Siena Facoltà di Ingegneria Motivating Problem #1 Motivating Problem #1 Hybrid Systems Hybrid Systems Computer Control GOAL: GOAL Science Theory command gear ratio, gas pedal, and brakes to trac ack k Finite Continuous a desired speed and minimize state dynamical consumptions systems machines B Hybrid systems A B C u(t) y(t) system CHALLE LLENG NGES: B C • continuous and discrete inputs • dynamics depends on gear C • nonlinear torque/speed maps A
Key Requirements for Hybrid Models Key Requirements for Hybrid Models Piecewise Affine Systems Piecewise Affine Systems (Sontag 1981) state+input space • Des Descriptive enough to capture the behavior of the system – continuous dynamics (physical laws) – logic components (switches, automata, software code) – interconnection between logic and dynamics • Si Simple enough for solving analysis and synthesis problems • Approximates nonlinear dynamics arbitrarily well linear systems nonlinear systems ? • Suitable for stability analysis, reachability analysis (verification), controller synthesis, ... linear hybrid systems Discrete Hybrid Automata Discrete Hybrid Automata Discrete Hybrid Automata Discrete Hybrid Automata (Torrisi, Bemporad, 2003) (Torrisi, Bemporad, 2003) Switched Affine System
Discrete Hybrid Automata Discrete Hybrid Automata Discrete Hybrid Automata Discrete Hybrid Automata (Torrisi, Bemporad, 2003) (Torrisi, Bemporad, 2003) Finite State Machine Discrete dynamics evolving according to a Boolean state update function Event Generator Discrete Hybrid Automata Discrete Hybrid Automata Logic and Inequalities Logic and Inequalities (Torrisi, Bemporad, 2003) Glover 1975, Williams 1977 Mode Selector a Boolean function selects the active mode i ( k ) of the SAS
Logic → → Inequalities: Symbolic Approach Inequalities: Symbolic Approach Logic → Inequalities: Geometric Approach Logic Logic → Inequalities: Geometric Approach 0. Given a Boolean statement F ( X 1 , X 2 , . . . , X n ) P , { î : Aî ô B } Geometric approach: The polytope is the T convex hull of the rows of the truth table 1. Convert to Conjunctive Normal Form (CNF): ð ñ V W W m ö i i ∈ P j X i i ∈ N j X j =1 2. Transform into inequalities: X X Aî ô B, î ∈ { 0 , 1 } n î i + (1 à î i ) 1 ô i ∈ P 1 i ∈ N 1 . . . . . . Aî ô B, î ∈ { 0 , 1 } . . . X X Every logic proposition can be translated into 1 ô î i + (1 à î i ) linear integer inequalities i ∈ P m i ∈ N m Every logic proposition can be translated into linear integer inequalities Mixed Logical Dynamical Systems Mixed Logical Dynamical Systems Logic → Logic → Inequalities: Geometric Approach Inequalities: Geometric Approach Example: logic “ AND ” 3 DHA 2 Mixed Logical Dynamical (MLD) Systems Key idea: 1 White points cannot be in the hull of black points (Bemporad, Morari 1999) " # " # " # " # ! à î 1 + î 3 ô 0 0 0 1 1 conv , , , = î : à î 2 + î 3 ô 0 0 1 0 1 Continuous and î 1 + î 2 à î 3 ô 1 0 0 0 1 binary variables • Computationally oriented (Mixed Integer Programming) Convex hull algorithms : cdd, lrs, qhull, chD, Hull, Porto • Suitable for optimal controller synthesis, verification, ...
A Simple Example A Simple Example HYSDEL HYSDEL ú (HYbrid ( HYbrid Systems Systems DEscription DEscription Language) Language) 0 . 8 x ( t ) + u ( t ) if x ( t ) õ 0 • System: x ( t + 1) = à 0 . 8 x ( t ) + u ( t ) if x ( t ) < 0 • Describe hybrid systems: à 10 ô x ( t ) ô 10 , à 1 ô u ( t ) ô 1 • Associate [ î ( t ) = 1] ↔ [ x ( t ) õ 0] and transform – Automata – Logic à mî ( t ) ô x ( t ) à m M = à m = 10 ï > 0 à ( M + ï ) î ( t ) ô à x ( t ) à ï small – Lin. Dynamics – Interfaces • Then x ( t + 1) = 1 . 6 î ( t ) x ( t ) à 0 . 8 x ( t ) + u ( t ) – Constraints z ( t ) ô Mî ( t ) (Torrisi, Bemporad, 2003) z ( t ) = î ( t ) x ( t ) z ( t ) õ mî ( t ) z ( t ) ô x ( t ) à m (1 à î ( t )) • Automatically generate MLD models in Matlab z ( t ) õ x ( t ) à M (1 à î ( t )) • Rewrite as a linear equation x ( t + 1) = 1 . 6 z ( t ) à 0 . 8 x ( t ) + u ( t ) Download: http://www.dii.unisi.it/~bemporad/tools.html http://control.ethz.ch/~hybrid/hysdel Example 1: AD section Example 1: AD section Example 2: DA section Example 2: DA section [ ] [ ] Nonlinear amplification unit = ↔ ≥ s T h h max SYSTEM tank { < u ( u u ) INTERFACE { = t u STATE { comp − ≥ REAL h [-0.3,0.3]; } 2.3 u 1.3 u ( u u ) t t INPUT { REAL Q [-10,10]; } PARAMETER { REAL k = 1; REAL e = 1e-6; } } /* end interface */ IMPLEMENTATION { SYSTEM motor { INTERFACE { AUX { IMPLEMENTATION { REAL unl; STATE { AUX { BOOL th; } REAL ucomp; } BOOL s; } AD { INPUT { REAL u [0,10]; } th = ut - u <= 0; } AD { s = hmax - h <= 0; } PARAMETER { DA { REAL ut = 1; CONTINUOUS { unl = { IF th THEN 2.3*u - 1.3*ut REAL e = 1e-6;} h = h + k * Q; } } /* end interface */ ELSE u }; } } /* end implementation */ } /* end system */ CONTINUOUS { ucomp = unl; } } /* end implementation */ } /* end system */
Example 3: LOGIC section Example 3: LOGIC section Example 4: CONTINUOUS section Example 4: CONTINUOUS section SYSTEM train { INTERFACE { STATE { SYSTEM capacitorD { BOOL brake; } INTERFACE { INPUT { STATE { BOOL alarm, tunnel, fire; } REAL u; } PARAMETER { } /* end interface */ REAL R = 1e4; REAL C = 1e-4; d REAL T = 1e-1; } IMPLEMENTATION { = } /* end interface */ i C u t ( ) AUX { dt BOOL decision; } IMPLEMENTATION { LOGIC { decision = CONTINUOUS { Apply forward difference rule: alarm & (~tunnel | ~fire); } u = u - T/C/R*i; } = ∧ ¬ ∨ ¬ u u ( s s ) AUTOMATA { T } /* end implementation */ brake alarm tunnel fire brake = decision; } + = + u k ( 1) u k ( ) i k ( ) } /* end system */ MUST { → s u C fire -> alarm; } fire alarm } /* end implementation */ } /* end system */ Example 5: AUTOMATA section Example 5: AUTOMATA section Example 6: MUST section Example 6: MUST section SYSTEM watertank { INTERFACE { STATE { REAL h; } INPUT { SYSTEM outflow { REAL Q; } INTERFACE { PARAMETER { STATE { REAL hmax = 0.3; BOOL closing, stop, opening; } REAL k = 1; } INPUT { } /* end interface */ BOOL uclose, uopen, ustop; } } /* end of interface */ IMPLEMENTATION { IMPLEMENTATION { CONTINUOUS { h = h + k*Q; } AUTOMATA { closing = (uclose & closing) | (uclose & stop); MUST { stop = ustop | (uopen & closing) | (uclose & opening); h - hmax <= 0; opening = (uopen & stop) | (uopen & opening); } -h <= 0; } MUST { ≤ ≤ 0 h h } /* end implementation */ ~(uclose & uopen); } /* end system */ max ~(uclose & ustop); ~(uopen & ustop); } } /* end implementation */ } /* end system */
Modeling Flow Modeling Flow Example: Bouncing Ball Example: Bouncing Ball g 12 x ( t ) + h 12 u ( t ) < k 12 x g 23 x ( t ) + h 23 u ( t ) < k 23 x ¨ = à g x ( t + 1) = x ( t + 1) = x ( t + 1) = A 1 x ( t ) + B 1 u ( t ) + f 1 A 3 x ( t ) + B 3 u ( t ) + f 3 A 2 x ( t ) + B 2 u ( t ) + f 2 ç( t + ) = à (1 à ë ) x ç ( t à ) x ô 0 ⇒ x g 13 x ( t ) + h 13 u ( t ) < k 13 g 32 x ( t ) + h 32 u ( t ) < k 32 Designer ë ∈ [0 , 1] N F= m g HYSDEL Source Hysdel logic MLD How to model this system in MLD form? PWA A/D D/A Mixed Piecewise Logical continuous Affine form Dynamical form HYSDEL - HYSDEL - Bouncing Ball Bouncing Ball System Theory for Hybrid Systems System Theory for Hybrid Systems SYSTEM bouncing_ball { INTERFACE { /* Description of variables and constants */ • Analysis STATE { REAL height [-10,10]; REAL velocity [-100,100]; } – Well-posedness – Realization & Transformation PARAMETER { REAL g=9.8; – Reachability (=Verification) REAL dissipation=.4; /* 0=elastic, 1=completely anelastic */ – Observability REAL Ts=.05; } } – Stability IMPLEMENTATION { AUX { REAL z1; REAL z2; BOOL negative; } • Synthesis AD { negative = height <= 0; } – Control DA { z1 = { IF negative THEN height-Ts*velocity – State estimation ELSE height+Ts*velocity-Ts*Ts*g}; z2 = { IF negative THEN -(1-dissipation)*velocity – Identification ELSE velocity-Ts*g}; } – Modeling language CONTINUOUS { height = z1; velocity=z2;} }}
Recommend
More recommend