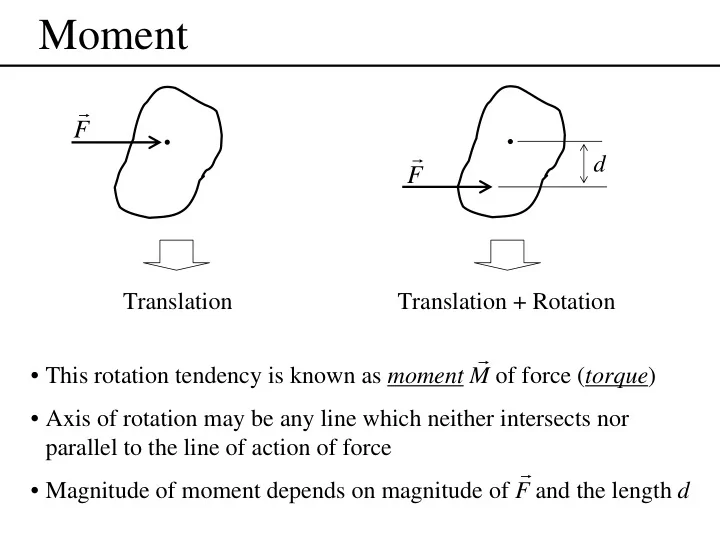
Moment r F r d F Translation Translation + Rotation r This - PowerPoint PPT Presentation

Moment r F r d F Translation Translation + Rotation r • This rotation tendency is known as moment M of force ( torque ) • Axis of rotation may be any line which neither intersects nor parallel to the line of action of force r • Magnitude of moment depends on magnitude of F and the length d

Mathematical definition Moment about axis O-O is defined as O r r F M = Fd M (N.m) α r Moment is a vector A Direction, normal to r - F plane (right d hand rule) Axis O-O is called moment axis O r F Moment is a sliding vector Μ= Fd 2-D A • Axis becomes point d • Use sign convention to express + direction (+ for CCW, − for CW)

The cross product r O r F The moment of about point A = r F M α r r r = × r M r F A d Magnitude M = Fr sin( α ) = Fd O • Direction: normal to the r – F plane, right hand rule × = ˆ ˆ ˆ • xyz axis have to satisfy the right hand rule; i j k r r r r × ≠ × r F F r • Sequence of r and F is important;

Varignon’s theorem The moment of a The moment of the components = force about any point of the force about the same point r r r r r = + F F F F F 1 2 1 r r r r r r = × = × + M o r F r ( F F ) r 1 2 A r r r O r r r = × + × F M o r F r F 2 1 2 r r F F y Useful with rectangular components r F M o = F x d 2 -F y d 1 d 2 x y O d 1 Can use with more than 2 components + x

Sample (1) Calculate the magnitude of the moment about the base point O of the 600-N force.

Sample (2) The force exerted by the plunger of cylinder AB on the door is 40 N directed along the line AB , and this force tends to keep the door closed. Compute the moment of this force about the hinge O . What force F c normal to the plane of the door must the door stop at C exert on the door so that the combined moment about O of the two forces is zero?

Couple (1) Couple is a moment produced by two equal, d opposite, and noncollinear forces. a M = F ( a + d ) – Fa = Fd r r − F The moment of a couple has the same value F O + for all moment centers r r r r r r r r = × + × − = − × r M r F r ( F ) ( r r ) F A B A B M r r r = × M r F r A r r r A B r r − • Couple may be represented as a free vector r F O B r F • Direction of couple is normal to the plane of two force

Couple (2) M M M M CCW couple CW couple Since couple is a free vector, the followings are equivalent couples r r r r M M M M d F F d/2 ≡ ≡ ≡ 2F F F F 2F F

Force-couple systems A given force can be replaced by an equal parallel force and a couple. Add to the system r F r − F B B B ≡ ≡ M=Fd r d r F F A A A Force-couple system r F r − F B d r No changes in the F Couple net external effect A

Sample (3) The rigid structural member is subjected to a couple consisting of the two 100-N forces. Replace this couple by an equivalent couple consisting of the two forces P and –P , each of which has a magnitude of 400 N. Determine the proper angle θ .

Sample (4) Replace the horizontal 400-N force acting on the lever by an equivalent system consisting of a force at O and a couple.

Sample (5) Calculate the moment of the 1200-N force about pin A of the bracket. Begin by replacing the 1200-N force by a force-couple system at point C .

Sample (6) 1.6 m 0.8 m Determine the combined moment M A about point A due to the two 0.8 m equal tensions T = 8 kN in the cable T acting on the pulley. Is it necessary C to know the pulley diameter? 45 ° T 1.6 m B A

Resultants The Resultant is the simplest force combination which can replace the original forces without altering the external effect on the body r y r r F 3 F y 2 F F 3 1 F 2 y r r r F 2 R F R r y 1 F R 1 y r θ R 1 x r r F F 2 F 3 R 1 x x x F 1 3 R x r r r r r r r r ∑ = + + + = + = ... R F F F F F F R (1) 1 2 3 2 3 1 r r r + = ∑ ∑ ∑ = = + R F R (2) 2 2 R F , R ( F ) ( F ) 1 1 x x x y ∑ = − θ = tan 1 R F ( R y R / ) y y x

Method to get a resultant r F 1 r r r ∑ M o = Σ ( F i d i = F R F 2 d ) O O 1 d d 2 3 r F 3 1) Pick a point (easy 3) Add forces and moments to find moment r r arms) F R F 1 d 1 1 r M o =Rd F 2 O d=M o /R r O F 3 F 2 d 2 F 3 d 3 2) Replace each force with a 4) Replace force-couple force at point O + a couple system with a single force

Other cases r r F F 1 1 r r r + = − F F F r 1 2 3 r F 2 F 2 O r r F d 3 F 3 r r ∑ ∑ = 0 = 0 F M O r r ∑ = = = ⋅ R F R M F d 3 O

Sample (7) Determine the resultant of the four forces and one couple that act on the plate shown.

Sample (8) Determine and locate the resultant R of the two force and one couple acting on the I-beam.

Sample (9) The five vertical loads represent the effect of the weights of the truss and supported roofing materials. The 400-N load represents the effect of wind pressure. Determine the equivalent force-couple system at A . Also, compute the x -intercept of the line of action of the system resultant treated as a single force R .

Sample (10) Replace the three forces acting on the bent pipe by a single equivalent force R . Specify the distance x from point O to the point on the x -axis through which the line of action of R passes.