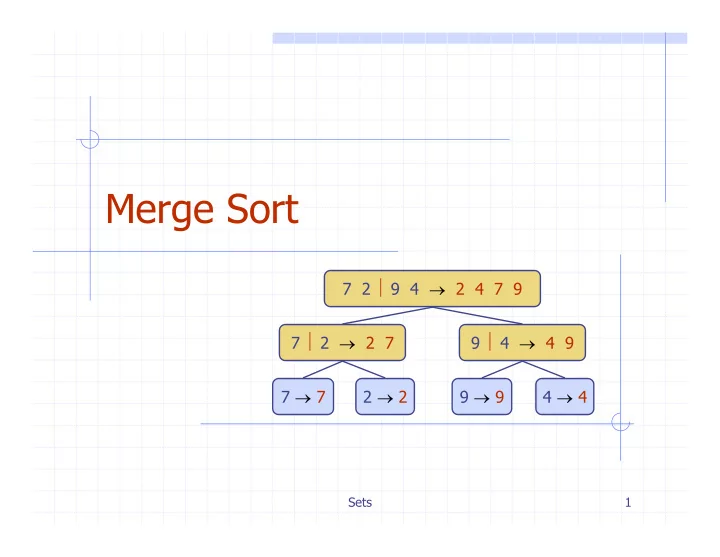
Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 - PowerPoint PPT Presentation

Merge Sort 7 2 ⏐ 9 4 → 2 4 7 9 7 ⏐ 2 → 2 7 9 ⏐ 4 → 4 9 7 → 7 2 → 2 9 → 9 4 → 4 Sets 1

Outline and Reading Divide-and-conquer paradigm (§10.1.1) Merge-sort (§10.1) � Algorithm � Merging two sorted sequences � Merge-sort tree � Execution example � Analysis Generic merging and set operations (§10.2) Summary of sorting algorithms Sets 2

Divide-and-Conquer Divide-and conquer is a Merge-sort is a sorting general algorithm design algorithm based on the paradigm: divide-and-conquer paradigm � Divide: divide the input data S in two disjoint subsets S 1 Like heap-sort and S 2 � It uses a comparator � Recur: solve the � It has O ( n log n ) running subproblems associated time with S 1 and S 2 Unlike heap-sort � Conquer: combine the � It does not use an solutions for S 1 and S 2 into a auxiliary priority queue solution for S � It accesses data in a The base case for the sequential manner recursion are subproblems of (suitable to sort data on a size 0 or 1 disk) Sets 3

Merge-Sort Merge-sort on an input Algorithm mergeSort ( S, C ) sequence S with n Input sequence S with n elements consists of elements, comparator C three steps: Output sequence S sorted according to C � Divide: partition S into two sequences S 1 and S 2 if S.size () > 1 of about n / 2 elements ( S 1 , S 2 ) ← partition ( S , n /2) each mergeSort ( S 1 , C ) � Recur: recursively sort S 1 mergeSort ( S 2 , C ) and S 2 S ← merge ( S 1 , S 2 ) � Conquer: merge S 1 and S 2 into a unique sorted sequence Sets 4

Merging Two Sorted Sequences The conquer step of Algorithm merge ( A, B ) merge-sort consists Input sequences A and B with of merging two n / 2 elements each sorted sequences A Output sorted sequence of A ∪ B and B into a sorted S ← empty sequence sequence S while ¬ A.isEmpty () ∧ ¬ B.isEmpty () containing the union of the elements of A if A.first () .element () < B.first () .element () and B S.insertLast ( A.remove ( A.first ())) Merging two sorted else sequences, each S.insertLast ( B.remove ( B.first ())) with n / 2 elements while ¬ A.isEmpty () and implemented by S.insertLast ( A.remove ( A.first ())) means of a doubly while ¬ B.isEmpty () linked list, takes S.insertLast ( B.remove ( B.first ())) O ( n ) time return S Sets 5

Merge-Sort Tree An execution of merge-sort is depicted by a binary tree � each node represents a recursive call of merge-sort and stores � unsorted sequence before the execution and its partition � sorted sequence at the end of the execution � the root is the initial call � the leaves are calls on subsequences of size 0 or 1 7 2 ⏐ 9 4 → 2 4 7 9 7 ⏐ 2 → 2 7 9 ⏐ 4 → 4 9 7 → 7 2 → 2 9 → 9 4 → 4 Sets 6

Execution Example Partition 7 2 9 4 ⏐ 3 8 6 1 → 1 2 3 4 6 7 8 9 7 2 9 4 → 2 4 7 9 3 8 6 1 → 1 3 8 6 7 2 → 2 7 9 4 → 4 9 3 8 → 3 8 6 1 → 1 6 7 → 7 2 → 2 9 → 9 4 → 4 3 → 3 8 → 8 6 → 6 1 → 1 Sets 7

Execution Example (cont.) Recursive call, partition 7 2 9 4 ⏐ 3 8 6 1 → 1 2 3 4 6 7 8 9 7 2 ⏐ 9 4 → 2 4 7 9 3 8 6 1 → 1 3 8 6 7 2 → 2 7 9 4 → 4 9 3 8 → 3 8 6 1 → 1 6 7 → 7 2 → 2 9 → 9 4 → 4 3 → 3 8 → 8 6 → 6 1 → 1 Sets 8

Execution Example (cont.) Recursive call, partition 7 2 9 4 ⏐ 3 8 6 1 → 1 2 3 4 6 7 8 9 7 2 ⏐ 9 4 → 2 4 7 9 3 8 6 1 → 1 3 8 6 7 ⏐ 2 → 2 7 9 4 → 4 9 3 8 → 3 8 6 1 → 1 6 7 → 7 2 → 2 9 → 9 4 → 4 3 → 3 8 → 8 6 → 6 1 → 1 Sets 9

Execution Example (cont.) Recursive call, base case 7 2 9 4 ⏐ 3 8 6 1 → 1 2 3 4 6 7 8 9 7 2 ⏐ 9 4 → 2 4 7 9 3 8 6 1 → 1 3 8 6 7 ⏐ 2 → 2 7 9 4 → 4 9 3 8 → 3 8 6 1 → 1 6 7 → 7 2 → 2 9 → 9 4 → 4 3 → 3 8 → 8 6 → 6 1 → 1 Sets 10

Execution Example (cont.) Recursive call, base case 7 2 9 4 ⏐ 3 8 6 1 → 1 2 3 4 6 7 8 9 7 2 ⏐ 9 4 → 2 4 7 9 3 8 6 1 → 1 3 8 6 7 ⏐ 2 → 2 7 9 4 → 4 9 3 8 → 3 8 6 1 → 1 6 7 → 7 2 → 2 9 → 9 4 → 4 3 → 3 8 → 8 6 → 6 1 → 1 Sets 11

Execution Example (cont.) Merge 7 2 9 4 ⏐ 3 8 6 1 → 1 2 3 4 6 7 8 9 7 2 ⏐ 9 4 → 2 4 7 9 3 8 6 1 → 1 3 8 6 7 ⏐ 2 → 2 7 9 4 → 4 9 3 8 → 3 8 6 1 → 1 6 7 → 7 2 → 2 9 → 9 4 → 4 3 → 3 8 → 8 6 → 6 1 → 1 Sets 12

Execution Example (cont.) Recursive call, …, base case, merge 7 2 9 4 ⏐ 3 8 6 1 → 1 2 3 4 6 7 8 9 7 2 ⏐ 9 4 → 2 4 7 9 3 8 6 1 → 1 3 8 6 7 ⏐ 2 → 2 7 9 4 → 4 9 3 8 → 3 8 6 1 → 1 6 7 → 7 2 → 2 9 → 9 4 → 4 3 → 3 8 → 8 6 → 6 1 → 1 Sets 13

Execution Example (cont.) Merge 7 2 9 4 ⏐ 3 8 6 1 → 1 2 3 4 6 7 8 9 7 2 ⏐ 9 4 → 2 4 7 9 3 8 6 1 → 1 3 8 6 7 ⏐ 2 → 2 7 9 4 → 4 9 3 8 → 3 8 6 1 → 1 6 7 → 7 2 → 2 9 → 9 4 → 4 3 → 3 8 → 8 6 → 6 1 → 1 Sets 14

Execution Example (cont.) Recursive call, …, merge, merge 7 2 9 4 ⏐ 3 8 6 1 → 1 2 3 4 6 7 8 9 7 2 ⏐ 9 4 → 2 4 7 9 3 8 6 1 → 1 3 6 8 7 ⏐ 2 → 2 7 9 4 → 4 9 3 8 → 3 8 6 1 → 1 6 7 → 7 2 → 2 9 → 9 4 → 4 3 → 3 8 → 8 6 → 6 1 → 1 Sets 15

Execution Example (cont.) Merge 7 2 9 4 ⏐ 3 8 6 1 → 1 2 3 4 6 7 8 9 7 2 ⏐ 9 4 → 2 4 7 9 3 8 6 1 → 1 3 6 8 7 ⏐ 2 → 2 7 9 4 → 4 9 3 8 → 3 8 6 1 → 1 6 7 → 7 2 → 2 9 → 9 4 → 4 3 → 3 8 → 8 6 → 6 1 → 1 Sets 16

Analysis of Merge-Sort The height h of the merge-sort tree is O (log n ) � at each recursive call we divide in half the sequence, The overall amount or work done at the nodes of depth i is O ( n ) � we partition and merge 2 i sequences of size n / 2 i � we make 2 i + 1 recursive calls Thus, the total running time of merge-sort is O ( n log n ) depth #seqs size 0 1 n n / 2 1 2 n / 2 i 2 i i … … … Sets 17

Summary of Sorting Algorithms Algorithm Time Notes slow selection-sort in-place O ( n 2 ) for small data sets (< 1K) slow insertion-sort O ( n 2 ) in-place for small data sets (< 1K) fast heap-sort in-place O ( n log n ) for large data sets (1K — 1M) fast merge-sort sequential data access O ( n log n ) for huge data sets (> 1M) Sets 18

Sets Sets 19

Storing a Set in a List We can implement a set with a list Elements are stored sorted according to some canonical ordering The space used is O ( n ) Nodes storing set elements in order ∅ List Set elements Sets 20

Generic Merging (§10.2) Generalized merge Algorithm genericMerge ( A, B ) S ← empty sequence of two sorted lists while ¬ A.isEmpty () ∧ ¬ B.isEmpty () A and B a ← A.first () .element (); b ← B.first () .element () Template method if a < b genericMerge aIsLess ( a, S ); A.remove ( A.first ()) Auxiliary methods else if b < a bIsLess ( b, S ); B.remove ( B.first ()) � aIsLess else { b = a } � bIsLess bothEqual ( a, b, S ) � bothEqual A.remove ( A.first ()); B.remove ( B.first ()) Runs in O ( n A + n B ) while ¬ A.isEmpty () time provided the aIsLess ( a, S ); A.remove ( A.first ()) while ¬ B.isEmpty () auxiliary methods bIsLess ( b, S ); B.remove ( B.first ()) run in O (1) time return S Sets 21

Using Generic Merge for Set Operations Any of the set operations can be implemented using a generic merge For example: � For intersection: only copy elements that are duplicated in both list � For union: copy every element from both lists except for the duplicates All methods run in linear time. Sets 22

Set Operations We represent a set by the Set union: sorted sequence of its � aIsLess ( a, S ) elements S.insertFirst ( a ) By specializing the auxliliary � bIsLess ( b, S ) methods he generic merge S.insertLast ( b ) algorithm can be used to � bothAreEqual ( a, b, S ) perform basic set S. insertLast ( a ) operations: Set intersection: � union � aIsLess ( a, S ) � intersection { do nothing } � subtraction � bIsLess ( b, S ) The running time of an { do nothing } operation on sets A and B � bothAreEqual ( a, b, S ) should be at most O ( n A + n B ) S. insertLast ( a ) Sets 23

Quick-Sort 7 4 9 6 2 → 2 4 6 7 9 4 2 → 2 4 7 9 → 7 9 2 → 2 9 → 9 Sets 24

Outline and Reading Quick-sort (§10.3) � Algorithm � Partition step � Quick-sort tree � Execution example Analysis of quick-sort (§10.3.1) In-place quick-sort (§10.3.1) Summary of sorting algorithms Sets 25

Quick-Sort Quick-sort is a randomized sorting algorithm based x on the divide-and-conquer paradigm: � Divide: pick a random element x (called pivot) and x partition S into � L elements less than x � E elements equal x L E G � G elements greater than x � Recur: sort L and G � Conquer: join L , E and G x Sets 26