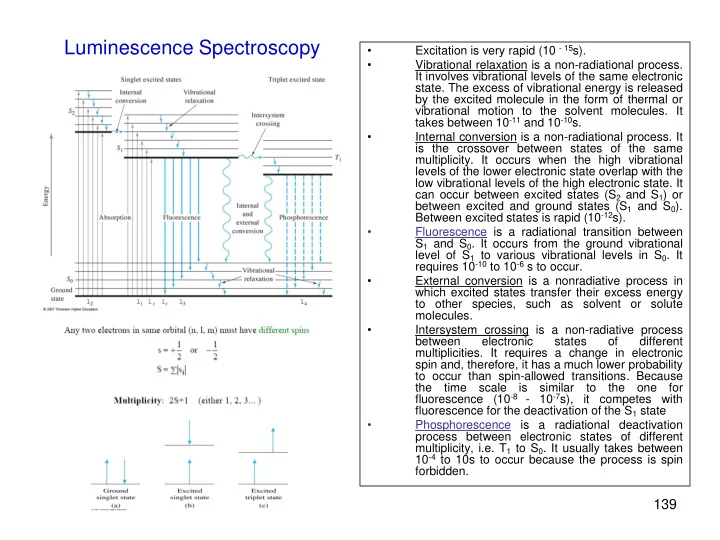

Luminescence Spectroscopy • Excitation is very rapid (10 - 15 s). • Vibrational relaxation is a non-radiational process. It involves vibrational levels of the same electronic state. The excess of vibrational energy is released by the excited molecule in the form of thermal or vibrational motion to the solvent molecules. It takes between 10 -11 and 10 -10 s. • Internal conversion is a non-radiational process. It is the crossover between states of the same multiplicity. It occurs when the high vibrational levels of the lower electronic state overlap with the low vibrational levels of the high electronic state. It can occur between excited states (S 2 and S 1 ) or between excited and ground states (S 1 and S 0 ). Between excited states is rapid (10 -12 s). • Fluorescence is a radiational transition between S 1 and S 0 . It occurs from the ground vibrational level of S 1 to various vibrational levels in S 0 . It requires 10 -10 to 10 -6 s to occur. • External conversion is a nonradiative process in which excited states transfer their excess energy to other species, such as solvent or solute molecules. • Intersystem crossing is a non-radiative process between electronic states of different multiplicities. It requires a change in electronic spin and, therefore, it has a much lower probability to occur than spin-allowed transitions. Because the time scale is similar to the one for fluorescence (10 -8 - 10 -7 s), it competes with fluorescence for the deactivation of the S 1 state • Phosphorescence is a radiational deactivation process between electronic states of different multiplicity, i.e. T 1 to S 0 . It usually takes between 10 -4 to 10s to occur because the process is spin forbidden. 139
Intensity of fluorescence (or phosphorescence) emission as a function of fluorophor (or phosphor) concentration • The power of fluorescence (or phosphorescence) radiation (F or P) is proportional to the radiant power of the excitation beam that is absorbed by the system: P 0 P F = K’(P 0 – P) (1) • The transmittance of the sample is given by Beer’s law: P/P 0 = 10 - e bc (2) • Re-arranging Eq. 1: F F = K’ P 0 (1 – P / P 0 ) • Substituting Eq. 2 above: Detector F = K’ (1 – 10 - e bc ) (3) • The exponential term in Eq. 3 can be expanded as a Maclaurin series to: F = K’ .P 0 .[2.303 e bc – (2.303 e bc) 2 + (2.303 e bc) 3 - … ] (4) 2! 3! LDR Intensity • For diluted solutions, i.e. 2.303ebc < 0.05, all of the subsequent terms in the brackets become negligible with respect to the first, so: F = K’ .P 0 .2.303 e bc or F = 2.303.P 0 . K’ . e bc (5) • A plot of fluorescence (or phosphorescence) intensity as a function of concentration should be linear up to a certain concentration. • Three are the main reasons for lack of linearity at high concentrations: Concentration a) 2.303ebc > 0.05 b) self-quenching c) self-absorption 140
Fluorescence quantum yield • The slope of the calibration curve is equal to 2.303.P 0 . K’ . e bc. • K’ is also known as the fluorescence quantum yield ( f F ). ki • The fluorescence quantum yield is the ratio between the number of photons emitted as fluorescence and the number of photons absorbed: f F = # of fluorescence photons # of absorbed photons kic • Fluorescence quantum yields may vary kf between zero and unity: 0 < f F < 1 The higher the quantum yield, the stronger kec the fluorescence emission. • In terms of rate constants, the fluorescence quantum yield is expressed as follows: f F = kf kf + ki + kec + kic + kpd +kd • Consider a dilute solution of a fluorescent species A whose concentration is [A] (in mol.L -1 ). A very short pulse of light at time 0 will bring a certain number of molecules A to the S 1 excited state by absorption of photons: A + h ν → A* • The excited molecules then return to S 0 , either radiatively or non-radiatively, or undergo intersystem crossing. As in classical kinetics, the rate of disappearance of excited molecules is expressed by the following differential equation: -d[A*] / dt = (kf + knr) [A*] knr = ki + kec + kic + kpd + kd are the rate constants of competing processes that ultimately 141 reduce the intensity of fluorescence. k units = s -1 .
Fluorescence lifetime • Integration of equation: -d[A*] / dt = (kf + knr) [A*] yields the time evolution of the concentration of excited molecules [A*]. • Let [A*] 0 be the concentration of excited molecules at time 0 resulting from the pulse light excitation. Integration leads to: [A*] = [A*] 0 exp(-t / t ) where t is the lifetime of the excited state S 1 . • The fluorescence lifetime is then given by: t = 1 / kf + knr • Typical fluorescence lifetimes are in the ns range. • Typical phosphorescence lifetimes are in the ms to s range. • The fluorescence (or phosphorescence lifetime) is the time needed for the concentration of excited molecules to decrease to 1/e of its original value. • The fluorescence lifetime correlates to the fluorescence quantum yield as follows: f f = kf. t 142
Excitation and emission spectra • Excitation spectra appear in the same wavelength region as absorption spectra. • However, it is important to keep in mind that absorption spectra are not the same as excitation spectra. • Fluorescence and phosphorescence spectra appear at longer wavelength regions than excitation spectra. • Phosphorescence spectra appear at longer wavelength regions than fluorescence spectra. • In some cases, it is possible to observe vibrational transitions in room-temperature fluorescence spectra. There are several parameters (many wavelengths and two lifetimes) for compound 143 identification.
Fluorescence and Structure • General rule: Most fluorescent compounds are aromatic. An increase in the extent of the p -electron system (i.e. the degree of conjugation) leads to a shift of the absorption and fluorescence spectra to longer wavelengths and an increase in the fluorescence quantum yield. • Example: Aromatic hydrocarbon Fluorescence Naphthalene ultraviolet Anthracene blue Naphthacene green red Pentacene • The lowest-lying transitions of aromatic hydrocarbons are of the p → p* type, which are characterized by high molar absorption coefficients and relatively high quantum fluorescence quantum yields. No fluorescence 144 Fluorescence
Substituted Aromatic Hydrocarbons • The effect of substituents on the fluorescence characteristics of aromatic hydrocarbons varies with the type of substituent. • Heavy atoms: the presence of heavy atoms (e.g. Br, I, etc.) results in fluorescence quenching (internal heavy atom effect) because of the increase probability of intersystem crossing (ISC). • Electron- donating : -OH, -OR, -NH 2 , -NHR, -NR 2 This type of substituent generally induces and increase in the molar absorption coefficient and a shift in both absorption and fluorescence spectra. • Electron-withdrawing substituents: carbonyl and nitro-compounds Carbonyl groups : There is no “general rule” . Their effect depends on the position of the substituent group in the aromatic ring. Nitro groups : No detectable fluorescence. 145
Rigidity Rigidity usually enhances fluorescence emission pH of solution Additional resonance forms lead to a more stable first excited state 146
Quenching • Quenching : nonradiative energy transfer from an excited species to other molecules. Fluorescence • Quenching results in deactivation of S 1 without quenching of quinine the emission of radiation causing a decrease in fluorescence intensity. sulfate as a function of • Types of quenching: dynamic, static and others. chloride concentration • Dynamic quenching: or collisional quenching requires contact between the excited species and the quenching agent. • Dynamic quenching is a diffusion controlled process. As such, its rate depends on the temperature and viscosity of the sample. • High temperatures and low viscosity promote dynamic quenching. • For dynamic quenching with a single quencher, the Stern-Volmer expression is valid: F 0 /F = 1 + K q [Q] Where F 0 and F are the fluorescence intensities in the absence and the presence of quencher, respectively. [Q] is the concentration of quencher (mols.L -1 ) and K q is the Stern-Volmer Oxygen sensors quenching constant. • O 2 is paramagnetic, i.e. The Stern-Volmer constant is defined as: its natural electronic K q = kq / kf + ki + kic configuration is the where kq is the rate constant for the quenching process (diffusion controlled). triplet state. • Static Quenching: the quencher and the When O 2 interacts with fluorophor in the ground state form a complex. the fluorophor, it The complex is no fluorescent (dark complex). promotes conversion • The Stern-Volmer equation is still valid but Kq in and deactivation of this case is the equilibrium constant for complex excited fluorophor formation: A + Q <=> AQ. • molecules. In static quenching, the fluorescence lifetime of the fluorophor is not affected. In dynamic Upon interaction, O 2 quenching, the fluorescence lifetime of the goes into the singlet fluorophor is affected. So, lifetime can be used state (diamagnetic). 147 to distinguish between dynamic and static quenching.
Instrumentation Typical spectrofluorometer (or spectrofluuorimeter) configuration Recording Recording excitation and synchronous emission spectra fluorescence spectra 148
Recommend
More recommend