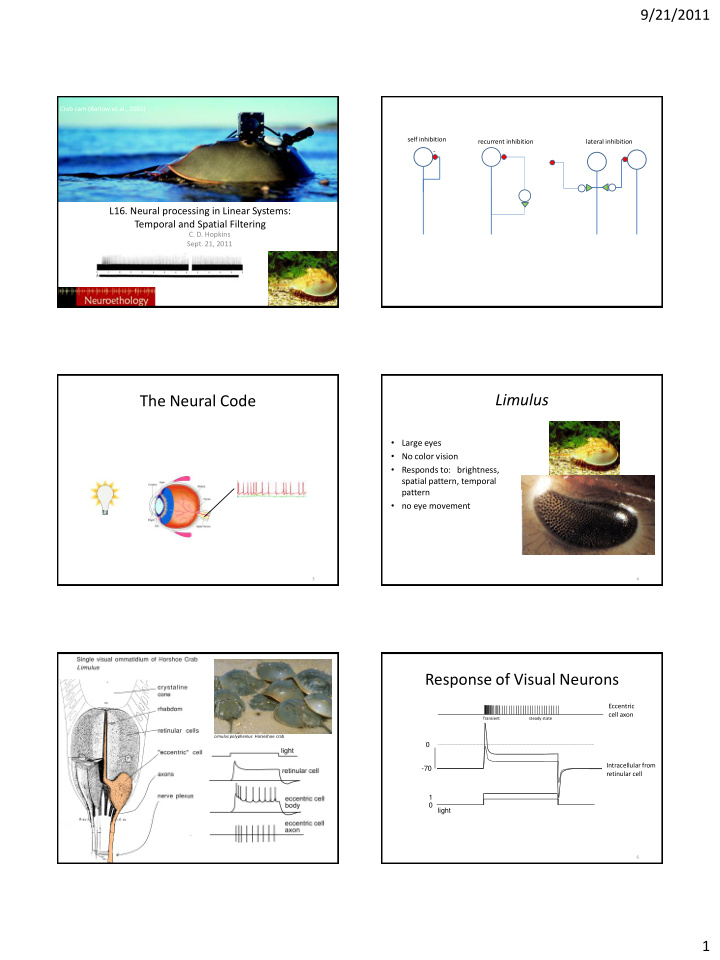
limulus
play

Limulus The Neural Code Large eyes No color vision Responds to: - PDF document

Jan 21, 2023 •307 likes •410 views

9/21/2011 Crab cam (Barlow et al., 2001) self inhibition recurrent inhibition lateral inhibition - L16. Neural processing in Linear Systems: Temporal and Spatial Filtering C. D. Hopkins Sept. 21, 2011 Limulus The Neural Code Large eyes

  1. 9/21/2011 Crab cam (Barlow et al., 2001) self inhibition recurrent inhibition lateral inhibition - L16. Neural processing in Linear Systems: Temporal and Spatial Filtering C. D. Hopkins Sept. 21, 2011 Limulus The Neural Code • Large eyes • No color vision • Responds to: brightness, spatial pattern, temporal pattern • no eye movement 3 4 Response of Visual Neurons Eccentric cell axon Transient steady state Limulus polyphemus Horseshoe crab 0 Intracellular from -70 retinular cell 1 0 light 5 6 1

  2. 9/21/2011 The Sensory Code for Stimulus Intensity is Spike Rate Limulus eye: a filter cascade. 1 cascade of filters light to 10 -2 voltage to out in voltage spike frequency 10 -4 transduction encoding and adaptation ----1 second--------- light on 8 7 Muscle stretch receptor transient steady state 9 10 Vestibular hair cell plus neuron Dynamic Range saturation damage threshold log linear range Stimulus intensity (log scale) 11 12 2

  3. 9/21/2011 Dynamic Response to Step Increase transient in Light Intensity adapted 1) Light increment 1 2) Light decrement 10 -2 adaptation symmetrical (codes both) 10 -4 ----1 second--------- light on 13 14 How can we characterize a complex sensory process like adaptation? self inhibition Sensory receptors, nerve cells, synapses, and simple circuits, - each act as stimulus filters. Can we think of each of these neural process as a well-behaved (predictable) filters? input output FILTER 15 Transfer function? Simple Stimuli Determine outputs for a known set of inputs. input output Clicks, Flashes Generate model Steps at each stage (neuron, Predict output to arbitrary synapse) , determine how the stimulus. input is changed. Sine waves, tone bursts 17 18 3

  4. 9/21/2011 The Real World: An arbitrary stimulus The Real World: An arbitrary stimulus For linear IN OUT Linear Systems Analysis systems……. X Y A system is “linear” if it obeys rules of response to impulse zero at t ~= 0 --superposition 1 at t=0 --scaling an impulse an impulse response h( t ) Given two valid inputs, x 1 (t), x 2 (t) as well as their respective outputs x(t) then a linear system must satisfy              y ( n ) h ( k ) x ( n k ) y ( t ) h ( ) x ( t ) d      k convolutio n 22 21 For linear For linear IN OUT IN OUT systems……. systems……. response to impulse response to impulse zero at t ~= 0 zero at t ~= 0 1 at t=0 1 at t=0 an impulse an impulse response h( t ) an impulse an impulse response h( t ) x(t) x(t)                           y ( n ) h ( k ) x ( n k ) y ( t ) h ( ) x ( t ) d y ( n ) h ( k ) x ( n k ) y ( t ) h ( ) x ( t ) d           k k convolutio n convolutio n 23 24 4

  5. 9/21/2011 For linear IN OUT Convolution in words and pictures systems……. Plot the impulse response response to impulse zero at t ~= 0 h(k), and the flipped and 1 at t=0 shifted input signal, x(n-k), an impulse response h( t ) an impulse on the same time axis. Calculate the product. Calculate the area under the x(t) product curve. Plot the summed area as function of the signal              shift. y ( t ) h ( ) x ( t ) d y ( n ) h ( k ) x ( n k )      k convolutio n jhu website 25 26 Slow Response, No inhibition Excitation, stronger Fast Response, Fast Response, inhibition No Inhibition Inhibition 27 28 Four Examples of Impulse Responses Dynamic Response to Step Increase in Light Intensity 1) Start in constant, low level light. Step increase in intensity for 2 sec. Decrease back to previous level. 2) Decrement in light intensity generates the reverse (mirror image) Time invariant, linear system. Good fit to curve predicted from convolution 29 30 5

  6. 9/21/2011 Convolution Result Predicts Dynamic Alternative methods for estimating h(t) Responses to Steps Response to impulse Response to noise Ringach,D. and R. Shapley (2004) Response to Cog. Sci. 28:147 component sine waves 31 Using Sine Wave Stimuli Do this for all relevant frequencies 1 Stimulate at all relevant ---Amplitude is multiplied by the frequencies with sinewave gain stimuli. gain ---Phase is delayed or advanced (add phase shift to sine wave) Measure gain and phase Amplitude and phase are different 0 for different frequencies. Frequency  phase  33 34 35 36 6

  7. 9/21/2011 Lateral Inhibition Lateral Inhibition also occurs in vertebrate retina Receptive Field of Mammalian Ganglion Cell (S. Kuffler, 1953) Open circles: spike frequency recorded from eccentric cell A, while A is given a step increase in light. Closed circles: constant illumination of ommatidium A while providing the step increase in light in B. light increase in area B 37 Steady State Response Lateral inhibition can be included in model Linear cascade from one cell What is the response to a converts light to spike point of light. frequency. Center (immediately over Spikes from one cell inhibit the eccentric cell): neighbors (lateral excitation . inhibition). Surround (adjacent areas): Inhibition is mutual (varies inhibition. with distance) 39 40 Lateral Inhibition Enhances Edges In two dimensions A Mexican Hat. Spatial impulse response. 41 42 7

  8. 9/21/2011 Prediction by Convolution step of light impulse response result 43 Tiger salamander Parallel Processing in Retina cone triad Salamander retina on electrode array. 1. rods 2 cones Meister M, Pine J, Baylor DA (1994) Multi-neuronal signals from the retina: 3 horizontal acquisition and analysis. J Neurosci Methods 51: 95 – 106. 4 bipolar 5 amacrine Wassle, Heinz (2004) Nat. Rev. Neurosci. 5: 747-57 6 ganglion stimulus visualization Meister M, Pine J, Baylor DA (1994) Multi-neuronal signals from the retina: acquisition and analysis. J Neurosci Methods 51: 95 – 106. 8

  9. 9/21/2011 Record simultaneously responses from 61 electrode array. Characterize receptive field (spatial and temporal) of each ganglion cell using flickering checkerboard. For one ganglion cell, center circular spot on receptive field; add surround grating. Contribution from On Bipolar cells: APB added to ringers prior to recording (blocks the metabotropic glutamate receptor, knocking out “on” pahtway. Sharp electrodes for recording from amacrine cells. Stimulus: circular spot, 800 microns diameter (slightly larger than RF. Surround flickering grating. Intensity changes every 30 ms, pseudorandom level variation. Grating flickers every .9 s. Lateral Inhibition 52 51 After convolution with mexican hat Mexican Hat 0 0 -1 0 0 0 -1 -2 -1 0 -1 -2 16 -2 -1 0 -1 -2 -1 0 0 0 -1 0 0 54 53 9

  10. 9/21/2011 Lessons from Visual Coding 1. The goal: understand sensory coding. Vision: example of The end “frequency code”. 2. Visual processing includes: 1. transduction, 2. encoding 3. Adaptation can be thought of as self inhibition. 4. Most sensory neurons behave as temporal filters: adaptation (tonic vs. phasic) 5. Linear systems analysis can also be used to describe spatial effects such as lateral inhibition. 6. Convolution can be used to predict responses to arbitrary stimuli. 55 10

More recommend