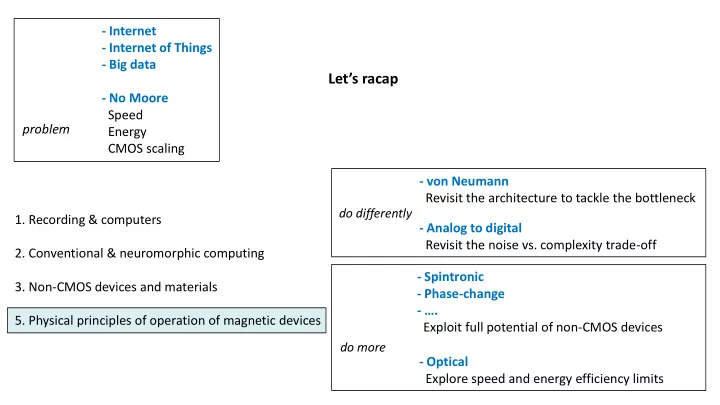

- Internet - Internet of Things - Big data Let’s racap - No Moore Speed problem Energy CMOS scaling - von Neumann Revisit the architecture to tackle the bottleneck do differently 1. Recording & computers - Analog to digital Revisit the noise vs. complexity trade-off 2. Conventional & neuromorphic computing - Spintronic 3. Non-CMOS devices and materials - Phase-change - …. 5. Physical principles of operation of magnetic devices Exploit full potential of non-CMOS devices do more - Optical Explore speed and energy efficiency limits
Anisotropic magnetoresistance Everspin Magnetic RAM MRAM 10ns & 1Gb Bipolar switching 1988 Giant magnetoresistance readout: dawn of spintronics 1998 IBM HDD read-head Review: Daughton, 2007 Grünberg & Fert Nobel Prize Thin Sol. Films ’ 92 100 kb AMR-MRAM R R Tunneling magnetoresistance Review: Chappert, Fert, Van Dau, Nature Mater. 6, 813 (2007) Moodera et al., PRL ‘95 Miyazaki & Tezuka JMMM ‘ 95
Everspin Magnetic RAM MRAM 10ns & 1Gb Bipolar switching 1998 Spin transfer torque writing MPU 2018 Everspin STT-MRAM CPU eMRAM SRAM 2013 Slonczewski & Berger Buckley Prize 16 Mb TMR-MRAM MRAM R R ~ HDD, Flash-SSD Tunneling magnetoresistance Review: Chappert, Fert, Van Dau, Nature Mater. 6, 813 (2007) Moodera et al., PRL ‘95 Miyazaki & Tezuka JMMM ‘ 95
Everspin Magnetic RAM MRAM 10ns & 1Gb Bipolar switching 2004 Spin Hall effect ~ ~ Kato, Awschalom et al. Science ‘04 Wunderlich, Kastner Sinova, TJ arXiv ’04, PRL ‘05 Review: Sinova , TJ et al. RMP ’15
Everspin Magnetic RAM MRAM 10ns & 1Gb Bipolar switching 2004 Spin Hall effect MPU CPU 2011 Spin orbit torque eMRAM 2016 Experimental chip (SPINTEC) eMRAM MRAM ~ ~ ~ HDD, Flash-SSD Kato, Awschalom et al. Science ‘04 Wunderlich, Kastner Sinova, TJ arXiv ’04, PRL ‘05 Miron et al. Nature ’ 11, Liu et al. Science ’ 12 Review: Sinova , TJ et al. RMP ’15 Review: Manchon , TJ et al. RMP‘19
Spin, Zeeman coupling, and spin-orbit coupling Relativistic QM: Dirac equation Classical E&M: Maxwell’s equations v E “B“ ~ v × E Spin- orbit = “Zeeman” felt in electron’s frame of reference Weak relativistic limit ⋯ ~1/𝑑 2 Schrödinger Zeeman Spin-orbit
Magnetoresistive readout ~ 1% anisotropic magnetoresistance ~ 10% tunneling magnetoresistance ~ 100% tunneling magnetoresistance Kelvin, 1857 Moodera, Miyazaki, Tezuka 1995 Grunberg, Fert 1988 Relativistic: Non-relativistic: Non-relativistic: spin-orbit scattering Majority and miniroty spin scattering Majority and minority density of states Review: Chappert, Fert, Van Dau, Nature Mater. 6, 813 (2007)
Writing by non-relativistic spin-transfer torque Transfer from carrier spin angular momentum to magnetization angular momentum CoFeB MgO CoFeB Slonczewski , JMMM ’96, Berger , PRB ’96 Review: Ralph & Stiles, JMMM ’ 08
Writing by non-relativistic spin-transfer torque - spin angular momentum transfer - spin precession CoFeB t s - spin decay MgO CoFeB Slonczewski , JMMM ’96, Berger , PRB ’96 Review: Ralph & Stiles, JMMM ’ 08
Writing by non-relativistic spin-transfer torque - spin angular momentum transfer - spin precession CoFeB t s - spin decay t s << t ex : t s >> t ex : MgO CoFeB Field-like torque Antidamping-like torque J crit ~ a Gilbert H aniso J crit ~ H aniso Slonczewski , JMMM ’96, Berger , PRB ’96 Review: Ralph & Stiles, JMMM ’ 08
Writing by relativistic spin-orbit torque Transfer from carrier linear momentum to spin angular momentum Co Reviews: TJ et al. RMP ’ 14 Kato, Awschalom et al. Science ’04, Wunderlich, Sinova, TJ et al. RMP ’ 15 Kastner Sinova, TJ arXiv ’04, PRL ’05, Manchon , TJ et al. RMP ‘19 Silov et al. APL ‘04, Ganichev et al. arXiv ’ 04, Pt Bernevig & Vafek, PRB ’0 5, Manchon & Zhang, PRB ’ 08, Chernyshev et al. Nature Phys.’09, Miron et al. Nature ’ 11, Liu et al. Science ‘12 Spin Hall effect Spin-orbit coupling & broken inversion symmetry GaMnAs Co Pt Inverse spin galvanic (Edelstein) effect
Writing by relativistic spin-orbit torque Transfer from carrier linear momentum to spin angular momentum Co 𝑒Ԧ 𝑒𝑢 = 𝑒 Ԧ 𝑡 𝑒𝑢 = 1 𝜏 Reviews: TJ et al. RMP ’ 14 𝑗ℎ [ Ԧ 𝜏, 𝐼 𝑓𝑦 + 𝐼 𝑡𝑝 ) Sinova, TJ et al. RMP ’ 15 Manchon , TJ et al. RMP ‘19 Pt 𝑒Ԧ 𝑒𝑢 = 0 ⟹ 𝐾 𝑓𝑦 𝑡 𝑡 = 1 ℎ 𝑁 × Ԧ 𝑗ℎ [ Ԧ 𝜏, 𝐼 𝑡𝑝 ] 𝑈 = 𝑒𝑁 𝑒𝑢 = 𝐾 𝑓𝑦 𝑡 = 1 Spin Hall effect ℎ 𝑁 × Ԧ 𝑗ℎ [ Ԧ 𝜏, 𝐼 𝑡𝑝 ] Spin-orbit coupling GaMnAs Co Pt Inverse spin galvanic (Edelstein) effect
Writing by relativistic spin-orbit torque Transfer from carrier linear momentum to spin angular momentum Co Reviews: TJ et al. RMP ’ 14 Sinova, TJ et al. RMP ’ 15 Manchon , TJ et al. RMP ‘19 Pt Spin Hall effect Spin-orbit coupling z z
Writing by relativistic spin-orbit torque Transfer from carrier linear momentum to spin angular momentum Reviews: TJ et al. RMP ’ 14 Sinova, TJ et al. RMP ’ 15 Manchon , TJ et al. RMP ‘19 Spin-orbit coupling GaMnAs Co Pt Inverse spin galvanic (Edelstein) effect
Louis Néel 1930‘s Tape recorder 1930‘s Antiferromagnetic exchange, local Néel molecular field Ferromagnetic exchange, global Weiss molecular field Paramagnetic no spontaneous order of spins Antiferromagnets Ferromagnetic Magnetic susceptibility Antiferromagnetic Né
Antiferromagnets AFs: Néel local molecular field, M =0 FMs: Weiss global molecular field, M Louis Néel 1930‘s
Antiferromagnets AFs: Néel local molecular field, M =0 Néel’s Nobel Lecture 1970 “Antiferromagnets are interesting and useless” Can’t write and read
Writing in antiferromagnets by relativistic spin-orbit torque Transfer from carrier linear momentum and spin angular momentum Spin-orbit coupling & local inversion asymmetry Anisotropic magnetoresistance readout R R Wadley , TJ et al., Science ’16 Review: TJ et al. Nature Nanotech ‘16 cf. AMR in FMs
Kittel PR ‘51 Writing speed: magnetic resonance frequency threshold Youtube channel: SLAC Ferromagnetic resonance ~GHz Antiferromagnetic resonance ~THz
Kittel PR ‘51 Writing speed: magnetic resonance frequency threshold H H A H : external + anisotropy field T H ,A T H T H = M ⨉ H T x ,A M M A T H H x : exchange field T x = M ⨉ H x M B Ferromagnetic resonance Antiferromagnetic resonance 𝑔 ~ 𝐼~ GHz 𝑔 ~ 𝐼𝐼 𝑦 ~ THz H B T x ,B T H ,B
Magnetoresistive readout in antiferromagnets Giant/tunneling magnetoresistance Anisotropic magnetoresistance readout R R in antiferromagnet ?? cf. GMR/TMR in FMs cf. AMR in FMs
Magneto-transport 𝑘 = ി Ԧ 𝜏 𝐹 Spatially averaged: Linear response: Onsager relations: 𝜏 𝑗𝑘 Ԧ 𝑡 = 𝜏 𝑘𝑗 −Ԧ 𝑡 𝑄ി 𝜏 = ി 𝜏 𝑢ി 𝜏 = ി 𝜏 Invariant under translation Invariant under inversion 𝜏 𝑦𝑦 𝜏 𝑦𝑧 𝜏 𝑦𝑨 s s s a a 𝜏 𝑦𝑦 𝜏 𝑦𝑧 𝜏 𝑦𝑨 0 𝜏 𝑦𝑧 𝜏 𝑦𝑨 𝜏 𝑧𝑦 𝜏 𝑧𝑧 𝜏 𝑧𝑨 = + s s s a a 𝜏 𝑦𝑧 𝜏 𝑧𝑧 𝜏 𝑧𝑨 −𝜏 𝑦𝑧 0 𝜏 𝑧𝑨 𝜏 𝑨𝑦 𝜏 𝑨𝑧 𝜏 𝑨𝑨 s s s a a 𝜏 𝑦𝑨 𝜏 𝑧𝑨 𝜏 𝑨𝑨 −𝜏 𝑦𝑨 −𝜏 𝑧𝑨 0 Anisotropic magnetoresistance Spontaneous Hall effect 𝑈𝜏 s Ԧ 𝑡 = 𝜏 s −Ԧ 𝑡 = 𝜏 s Ԧ 𝑡 𝑘 𝐼 = ℎ × 𝐹 Invariant under time (spin)-reversal a , 𝜏 𝑦𝑨 a , 𝜏 𝑧𝑦 a ) ℎ = (𝜏 𝑨𝑧 Hall (pseudo)-vector 𝑈ℎ Ԧ 𝑡 = ℎ −Ԧ 𝑡 = −ℎ Ԧ 𝑡 Odd under time (spin)-reversal
Magneto-transport – spontaneous Hall effect 𝑘 = ി Ԧ 𝜏 𝐹 Spatially averaged: Linear response: Onsager relations: 𝜏 𝑗𝑘 Ԧ 𝑡 = 𝜏 𝑘𝑗 −Ԧ 𝑡 𝑄ി 𝜏 = ി 𝜏 𝑢ി 𝜏 = ി 𝜏 Invariant under translation Invariant under inversion 𝜏 𝑦𝑦 𝜏 𝑦𝑧 𝜏 𝑦𝑨 s s s a a 𝜏 𝑦𝑦 𝜏 𝑦𝑧 𝜏 𝑦𝑨 0 𝜏 𝑦𝑧 𝜏 𝑦𝑨 𝜏 𝑧𝑦 𝜏 𝑧𝑧 𝜏 𝑧𝑨 = + s s s a a 𝜏 𝑦𝑧 𝜏 𝑧𝑧 𝜏 𝑧𝑨 −𝜏 𝑦𝑧 0 𝜏 𝑧𝑨 𝜏 𝑨𝑦 𝜏 𝑨𝑧 𝜏 𝑨𝑨 s s s a a 𝜏 𝑦𝑨 𝜏 𝑧𝑨 𝜏 𝑨𝑨 −𝜏 𝑦𝑨 −𝜏 𝑧𝑨 0 Anisotropic magnetoresistance Spontaneous Hall effect 𝑈𝜏 s Ԧ 𝑡 = 𝜏 s −Ԧ 𝑡 = 𝜏 s Ԧ 𝑡 𝑘 𝐼 = ℎ × 𝐹 Invariant under time (spin)-reversal a , 𝜏 𝑦𝑨 a , 𝜏 𝑧𝑦 a ) ℎ = (𝜏 𝑨𝑧 Hall (pseudo)-vector 𝑈ℎ Ԧ 𝑡 = ℎ −Ԧ 𝑡 = −ℎ Ԧ 𝑡 Odd under time (spin)-reversal
Magneto-transport – spontaneous Hall effect Neumann‘s principle (1885): A physical property cannot have lower symmetry than the crystal Net ferromagnetic (pseudo)-vector Spontaneous Hall effect 𝑘 𝐼 = ℎ × 𝐹 a , 𝜏 𝑦𝑨 a , 𝜏 𝑧𝑦 a ) ℎ = (𝜏 𝑨𝑧 Hall (pseudo)-vector 𝑈ℎ Ԧ 𝑡 = ℎ −Ԧ 𝑡 = −ℎ Ԧ 𝑡 Odd under time (spin)-reversal Suzuki et al. Phys. Rev. B 95, 094406 (2017)
Recommend
More recommend