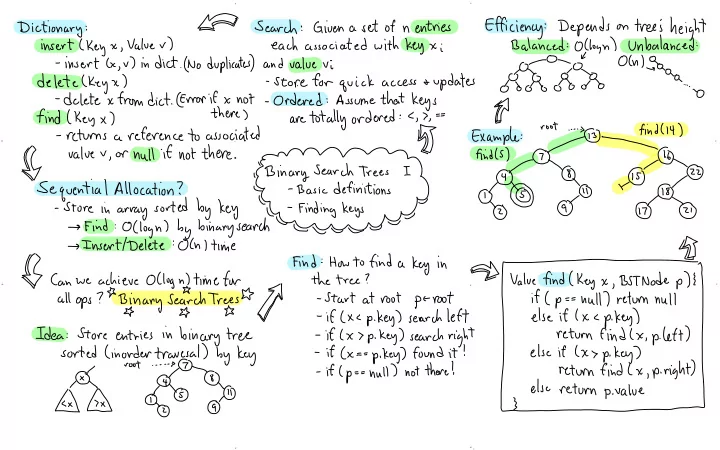

j n : Depends LAN Efficiency height on trees ' search : Giuenasetofn entries Dictionary : each associated with keyxi Balanced : Ollogn ) Unbalanced : insert ( key x. Valuer ) - insert Cx ,v ) - indict .( No duplicates ) ° " and value Vi off Qa - store for quick access sup dates delete ( Keyx ) gyu Gioro . . . Assume that keys - delete xfromdict . @ rrorifxnot ,o - ordered : are totally ordered :c , > , there ) find ( key x ) Example : X - root find ( 14 ) - returns a reference to associated > . . . . . . . valuer , or null if not there . ⑤ IYm.is?I!:I!ijntEoenssIuM.i , ④ find ' % sequential allocation ? ① - store in array sorted by key ' ⑨ ④ ④ → Find :O( login ) by binary search her - - u - , ' ÷ :÷÷÷÷÷÷÷÷÷÷÷÷÷÷ :# → Insert Delete ③ thine : : How to find a key in Find ::÷%i÷÷÷÷÷÷÷÷ t÷÷÷÷ :* : ' . Key ) search right - iflx > p sorted ( inordertravesal ) by key . key ) - if ( x - =p . key ) found it ! else it ( x > p , right ) root - → null ) not there ! - if ( p return find ( x ,p - - ⑦ else return p-value ④ , - e .
" > . insert " @dInsertCkey.x , Valuev ) Replacement Node ? - - find , ④ in tree In order successor ① x ④ ' ⑤ error ! duplicate ⑤ ' ④ - if found ⇒ 4¥ '# → ← delete ④ ' ④ Go ' ④ ① ' key ④ a - else copy . : create new node " ' ' in order ⑧ ' " fell out in order : " where predecesor successor we BSTNodeinsertfkeyx.ua/ueyBsTNodep# ' ⑧ ⑧ - null ) if ( p - - - . . . 3. ④ has two children . p= new Bst Node ( x ,v ) " " met " t Binary Search Trees I ? ? . key ) else if ( xcp ? ? " epithet : Find replacement node . right ) p.right-insertlx.ir , p , and then ④ , copy to ④ go.ee#*::::.::....osoia:ii:ii.oo . ⑧ why did we do : ? IQ error ?n%§? - else . left ) ? : remove this p.lett-insertlx.ir , p . ② ④ has single child node + restore " 4) in p Ist structure .io?.Q...pl.lett-- : ? mm . . . ( How ? - new BST Node insert " p ? - . left ) - inch ,v , pl Hurn p2 " " l l ' ' i - - - - - - - - - - s - - - - . .
- y :i÷÷' B '¥Yp÷÷nY¥ .in?i:;:%EEFi.YssI:PoLa97nYntp' Yoadeunentcnsrnoapftwparmmetmerinzteatikenvawe iioiii : :÷÷ii÷÷÷÷÷÷÷÷÷÷÷÷÷÷ :i :* I itt 's .fi?.Ieietecx.p.iea.s/whik!rr:kttFtmM.Bsfn%eB.iYnena . right extends comparable else PSTN oder =p types : isnt . :c ! ÷÷÷÷÷÷÷÷÷÷*÷÷ case is good Expected Thm : Ifn keys are inserted else ' in random order , expected height - find Replacement ( p ) re ! r - " ' 'm 'ff ④ ÷÷¥ contents top is Ullogn ) Example copy r 's : dug , . isphtsdekte .io?gijio.i.q&&gi9o?AnaiHospi:iatimsctm-d - is ① ' ⑨ . insert , delete ) run Examples : ⑨ d ' ' in ④ ⑥ , ⑨ och ) time , where h ' ④ ' ④ ④ ' ④ Q ⑦ - tree 's height ① IQ treplaammt ① ④ ④ ⑧
Recommend
More recommend