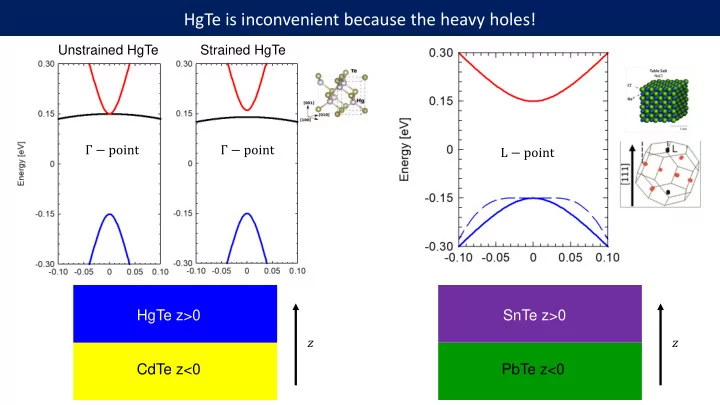
HgTe is inconvenient because the heavy holes! Unstrained HgTe - - PowerPoint PPT Presentation

β–Ά
hgte is inconvenient because the heavy holes
SMART_READER_LITE
LIVE PREVIEW

HgTe is inconvenient because the heavy holes! Unstrained HgTe - - PowerPoint PPT Presentation

Dec 04, 2023 192 likes β€’279 views

HgTe is inconvenient because the heavy holes! Unstrained HgTe Strained HgTe point point L point HgTe z>0 SnTe z>0 CdTe z<0 PbTe z<0 Surface states in IV-VI heterostructures Ideal -Dirac

slide-1
SLIDE 1

Strained HgTe Unstrained HgTe

HgTe is inconvenient because the heavy holes!

𝑨

HgTe z>0 CdTe z<0

Ξ“ βˆ’ point Ξ“ βˆ’ point 𝑨

SnTe z>0 PbTe z<0

L βˆ’ point

slide-2
SLIDE 2

Ξ” Ξ” ℏ𝑙𝑨𝑀 β„π‘™βˆ’π‘€ ℏ𝑙+𝑀 βˆ’β„π‘™π‘¨π‘€ ℏ𝑙𝑨𝑀 β„π‘™βˆ’π‘€ ℏ𝑙+𝑀 βˆ’β„π‘™π‘¨π‘€ – Ξ” – Ξ” 𝐹↑ 𝐹↓ 𝐼↑ 𝐼↓ 𝑨

SnTe z>0 Pb0.2Sn0.8Se PbSe z<0

Surface states in IV-VI heterostructures

𝐹 𝐼

β€œIdeal”-Dirac Hamiltonian Valid at low energy Orbital mixing very strong

PbTe

slide-3
SLIDE 3

SnTe PbTe Ξ” Ξ” ℏ𝑙𝑨𝑀 β„π‘™βˆ’π‘€ ℏ𝑙+𝑀 βˆ’β„π‘™π‘¨π‘€ ℏ𝑙𝑨𝑀 β„π‘™βˆ’π‘€ ℏ𝑙+𝑀 βˆ’β„π‘™π‘¨π‘€ – Ξ” – Ξ” |𝐹↑ > |𝐹↓ > |𝐼↑ > |𝐼↓ > 𝐹 = Ξ”2 + ℏ𝑙𝑨𝑀 2 + ℏ𝑙𝑠𝑀 2 Bulk solution Ξ” = βˆ’πΉ1 Ξ” = 𝐹2

slide-4
SLIDE 4

Ξ” Ξ” ℏ𝑙𝑨𝑀 β„π‘™βˆ’π‘€ ℏ𝑙+𝑀 βˆ’β„π‘™π‘¨π‘€ ℏ𝑙𝑨𝑀 β„π‘™βˆ’π‘€ ℏ𝑙+𝑀 βˆ’β„π‘™π‘¨π‘€ – Ξ” – Ξ” |𝐹↑ > |𝐹↓ > |𝐼↑ > |𝐼↓ > 𝑨

SnTe z>0 Pb0.2Sn0.8Se PbSe z<0

Ξ” = βˆ’πΉ1 πœ”(𝑦, 𝑧, 𝑨) = πœ“π‘“π‘—π‘™π‘¨π‘¨π‘“π‘—(𝑙𝑦𝑦+𝑙𝑧𝑧) 𝑙𝑨 = 𝑙1 Pb0.2Sn0.8Se: 𝐹 = Ξ”2 + ℏ𝑙𝑨𝑀 2 + ℏ𝑙𝑠𝑀 2 𝑙𝑠

2 = 𝑙𝑦 2 + 𝑙𝑧 2

Ξ” = 𝐹2 𝑙𝑨 = 𝑙2 𝑙1 = 𝐹2 βˆ’ 𝐹1

2 βˆ’ ℏ𝑙𝑠𝑀 2

ℏ𝑀 𝑙2 = 𝐹2 βˆ’ 𝐹2

2 βˆ’ ℏ𝑙𝑠𝑀 2

ℏ𝑀 PbSe: πœ”π‘„π‘π‘‡π‘“(0) = πœ”π‘„π‘π‘‡π‘œπ‘‡π‘“(0) ቀ π‘’πœ”π‘„π‘π‘‡π‘“ 𝐹2𝑒𝑨

𝑨=0

= βˆ’ ቀ π‘’πœ”π‘„π‘π‘‡π‘œπ‘‡π‘“ 𝐹1𝑒𝑨

𝑨=0

Boundary conditions:

slide-5
SLIDE 5

𝑙1

2

𝐹1

2 = 𝑙2 2

𝐹2

2

Bound Dirac state from boundary conditions

At z<0 𝐹± = Β± ℏ𝑀𝑙𝑠 𝑙1 = 𝐹2 βˆ’ 𝐹1

2 βˆ’ ℏ𝑙𝑠𝑀 2

ℏ𝑀 𝑙2 = 𝐹2 βˆ’ 𝐹2

2 βˆ’ ℏ𝑙𝑠𝑀 2

ℏ𝑀 𝑙1 = βˆ’πΉ1

2

ℏ𝑀 = 𝑗𝐹1 ℏ𝑀 𝑙2 = 𝑗𝐹2 ℏ𝑀 πœ”(𝑦, 𝑧, 𝑨) = πœ“1π‘“βˆ’π‘™1𝑨𝑓𝑗(𝑙𝑦𝑦+𝑙𝑧𝑧) πœ“2𝑓𝑙2𝑨𝑓𝑗(𝑙𝑦𝑦+𝑙𝑧𝑧) 𝑨 πœ” 2 PbSe

interface

PbSnSe

slide-6
SLIDE 6

Which one is topological PbSe or PbSnSe (HgTe or CdTe)

PbSe

interface

PbSnSe HgTe

slide-7
SLIDE 7

Observation of bound surface state – angle resolved photoemission

Pb0.9 Sn0.1Se Pb0.8 Sn0.2Se

Analytis et al .Phys. Rev. B 81, 205407 (2010)

  • Phys. Rev. Lett. 119 106602 (2017)

ARPES by group of O. Rader

Bi2Se3- 1 Dirac cones at gamma point