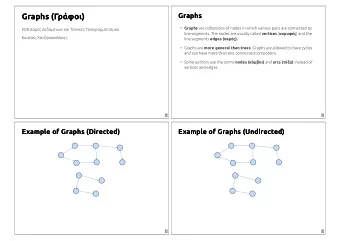
11/10/2016 What is a Graph? CSE373: Data Structures and Algorithms Graphs: Introduction Steve Tanimoto Autumn 2016 Which kind of graph are we going to study? This lecture material represents the work of multiple instructors at the University of Washington. Thank you to all who have contributed! Autumn 2016 CSE373: Data Structures & Algorithms 2 Graphs: the mathematical definition Undirected Graphs • A graph is a formalism for representing relationships among items • In undirected graphs, edges have no specific direction – Very general definition because very general concept – Edges are always “two-way” D • A graph is a pair Han Luke Degree(C)? G = (V,E) A C – A set of vertices, also known as nodes 3 Leia V = {v 1 ,v 2 ,…,v n } B – A set of edges V = {Han,Leia,Luke} E = {(Luke,Leia), E = {e 1 ,e 2 ,…,e m } Thus, (u,v) E implies (v,u) E (What do we call this property?) • (Han,Leia), • Each edge e i is a pair of vertices – Only one of these edges needs to be in the set (Leia,Han)} (v j ,v k ) – The other is implicit, so normalize how you check for it • An edge “connects” the vertices • Degree of a vertex: number of edges containing that vertex • Graphs can be directed or undirected – Put another way: the number of adjacent vertices Autumn 2016 CSE373: Data Structures & Algorithms 3 Autumn 2016 CSE373: Data Structures & Algorithms 4 Directed Graphs Self-Edges, Connectedness • In directed graphs (sometimes called digraphs), edges have a direction • A self-edge a.k.a. a loop is an edge of the form (u,u) D – Depending on the use/algorithm, a graph may have: A C • No self edges A or C • Some self edges 2 edges here B • All self edges (often therefore implicit, but we will be explicit) B • Thus, (u,v) E does not imply (v,u) E . • A node can have a degree / in-degree / out-degree of zero Let (u,v) E mean u → v • In-degree(B)? • A graph does not have to be connected • Call u the source and v the destination 2 – Even if every node has non-zero degree Out-degree(C)? • In-degree of a vertex: number of in-bound edges, i.e., edges where the vertex is the destination 2 • Out-degree of a vertex: number of out-bound edges This graph has 4 connected components. i.e., edges where the vertex is the source Autumn 2016 CSE373: Data Structures & Algorithms 5 Autumn 2016 CSE373: Data Structures & Algorithms 6 1
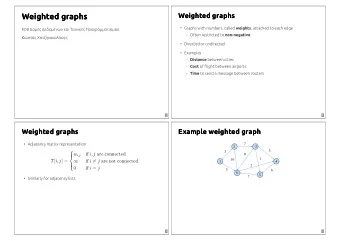
11/10/2016 D V = {A, B, C, D} More notation E = {(C, B), Examples A C (A, B), (B, A) Which would use directed edges? Which would have self-edges? (C, D)} For a graph G = (V,E) : B Which would be connected? Which could have 0-degree nodes? • |V| is the number of vertices 4+3+2+1 Dir Self Con Zero 1. Web pages with links • |E| is the number of edges 2. Facebook friends 0 – Minimum? 3. Methods in a program that call each other |V||V+1|/2 O (|V| 2 ) – Maximum for undirected? |V| 2 O (|V| 2 ) 4. Road maps (e.g., Google maps) – Maximum for directed? 5. Airline routes (assuming self-edges allowed, else subtract |V| ) 6. Family trees If (u,v) E • 7. Course pre-requisites – Then v is a neighbor of u , i.e., v is adjacent to u – Order matters for directed edges v u • u is not adjacent to v unless (v,u) E Autumn 2016 CSE373: Data Structures & Algorithms 7 Autumn 2016 CSE373: Data Structures & Algorithms 8 Weighted Graphs Examples • In a weighed graph, each edge has a weight a.k.a. cost What, if anything, might weights represent for each of these? – Typically numeric (most examples use ints) Do negative weights make sense? – Orthogonal to whether graph is directed – Some graphs allow negative weights ; many do not • Web pages with links 20 Clinton • Facebook friends Mukilteo • Methods in a program that call each other • Road maps (e.g., Google maps) 30 Kingston Edmonds • Airline routes • Family trees 35 Bainbridge • Course pre-requisites Seattle 60 Bremerton Autumn 2016 CSE373: Data Structures & Algorithms 9 Autumn 2016 CSE373: Data Structures & Algorithms 10 Paths and Cycles Path Length and Cost • Path length: Number of edges in a path A path is a list of vertices [v 0 ,v 1 ,…,v n ] such that (v i ,v i+1 ) • • Path cost: Sum of weights of edges in a path E for all 0 i < n. Say “a path from v 0 to v n ” Example where • A cycle is a path that begins and ends at the same node ( v 0 == v n ) P= [Seattle, Salt Lake City, Chicago, Dallas, San Francisco, Seattle] Chicago Chicago 3.5 Seattle Seattle 2 2 Salt Lake City length(P) = 5 Salt Lake City 2 2.5 cost(P) = 11.5 2.5 2.5 San Francisco Dallas 3 Example: [Seattle, Salt Lake City, Chicago, Dallas, San Francisco, Seattle] Dallas San Francisco Autumn 2016 CSE373: Data Structures & Algorithms 11 Autumn 2016 CSE373: Data Structures & Algorithms 12 2
11/10/2016 Simple Paths and Cycles Paths and Cycles in Directed Graphs • A simple path repeats no vertices, except the first might be the Example: D last [Seattle, Salt Lake City, San Francisco, Dallas] A [Seattle, Salt Lake City, San Francisco, Dallas, Seattle] C • Recall, a cycle is a path that ends where it begins B [Seattle, Salt Lake City, San Francisco, Dallas, Seattle] [Seattle, Salt Lake City, Seattle, Dallas, Seattle] No Is there a path from A to D? • A simple cycle is both a cycle and a simple path No [Seattle, Salt Lake City, San Francisco, Dallas, Seattle] Does the graph contain any cycles? Autumn 2016 CSE373: Data Structures & Algorithms 13 Autumn 2016 CSE373: Data Structures & Algorithms 14 Undirected-Graph Connectivity Directed-Graph Connectivity • An undirected graph is connected if for all • A directed graph is strongly connected if pairs of vertices u,v , there exists a path from u to v there is a path from every vertex to every other vertex • A directed graph is weakly connected if there is a path from every vertex to every Connected graph Disconnected graph other vertex ignoring direction of edges • An undirected graph is complete, a.k.a. fully connected if for all pairs of vertices u,v , there exists an edge from u to v • A complete a.k.a. fully connected directed graph has an edge from every vertex to every other vertex plus self edges plus self edges Autumn 2016 CSE373: Data Structures & Algorithms 15 Autumn 2016 CSE373: Data Structures & Algorithms 16 Rooted Trees Trees as Graphs • We are more accustomed to rooted trees where: – We identify a unique root When talking about graphs, – We think of edges as directed: parent to children we say a tree is a graph that is: – Undirected • Given a tree, picking a root gives a unique rooted tree – Acyclic – The tree is just drawn differently – Connected D E A B So all trees are graphs, but not redrawn all graphs are trees A B C C D E F F G H G H Autumn 2016 CSE373: Data Structures & Algorithms 17 Autumn 2016 CSE373: Data Structures & Algorithms 18 3
11/10/2016 Rooted Trees Directed Acyclic Graphs (DAGs) • We are more accustomed to rooted trees where: • A DAG is a directed graph with no (directed) cycles – We identify a unique root – Every rooted directed tree is a DAG – We think of edges as directed: parent to children – But not every DAG is a rooted directed tree • Given a tree, picking a root gives a unique rooted tree – The tree is just drawn differently D E F B G H C redrawn – Every DAG is a directed graph A A – But not every directed graph is a DAG C B F D E G H Autumn 2016 CSE373: Data Structures & Algorithms 19 Autumn 2016 CSE373: Data Structures & Algorithms 20 Examples Density / Sparsity Which of our directed-graph examples do you expect to be a DAG? • Let E be the set of edges and V the set of vertices. • Then 0 ≤ |E| ≤ |V| 2 • Web pages with links • And |E| is O (|V| 2 ) • Methods in a program that call each other • Because |E| is often much smaller than its maximum size, we do not • Airline routes always approximate |E| as O (|V| 2 ) • Family trees – This is a correct bound, it just is often not tight • Course pre-requisites – If it is tight, i.e., |E| is (|V| 2 ) we say the graph is dense • More sloppily, dense means “lots of edges” – If |E| is O (|V|) we say the graph is sparse • More sloppily, sparse means “most possible edges missing” Autumn 2016 CSE373: Data Structures & Algorithms 21 Autumn 2016 CSE373: Data Structures & Algorithms 22 What is the Data Structure? Adjacency Matrix • So graphs are really useful for lots of data and questions • Assign each node a number from 0 to |V|-1 – For example, “what’s the lowest-cost path from x to y” • A |V| x |V| matrix (i.e., 2-D array) of Booleans (or 1 vs. 0 ) – If M is the matrix, then M[u][v] being true • But we need a data structure that represents graphs means there is an edge from u to v • The “best one” can depend on: 0 1 2 3 – Properties of the graph (e.g., dense versus sparse) D(3) 0 F T F F – The common queries (e.g., “is (u,v) an edge?” versus “what are the neighbors of node u ?”) A(0) C(2) 1 T F F F • So we’ll discuss the two standard graph representations B(1) F T F T 2 – Adjacency Matrix and Adjacency List – Different trade-offs, particularly time versus space 3 F F F F Autumn 2016 CSE373: Data Structures & Algorithms 23 Autumn 2016 CSE373: Data Structures & Algorithms 24 4
Recommend
More recommend
