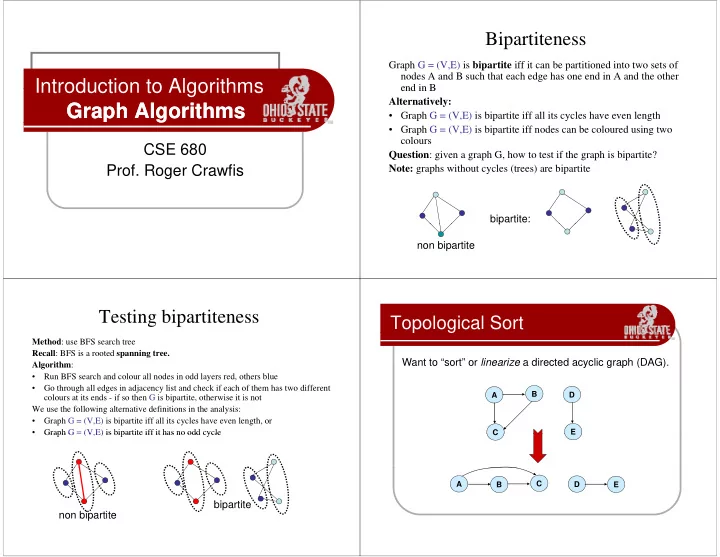
Bipartiteness Graph G = (V,E) is bipartite iff it can be partitioned into two sets of nodes A and B such that each edge has one end in A and the other Introduction to Algorithms Introduction to Algorithms end in B end in B Alternatively: Graph Algorithms Graph Algorithms g • Graph G = (V,E) is bipartite iff all its cycles have even length • Graph G = (V,E) is bipartite iff nodes can be coloured using two colours CSE 680 Question : given a graph G how to test if the graph is bipartite? Question : given a graph G, how to test if the graph is bipartite? Prof. Roger Crawfis Note: graphs without cycles (trees) are bipartite bipartite: p non bipartite Testing bipartiteness Topological Sort p g Method : use BFS search tree Recall : BFS is a rooted spanning tree. Want to “sort” or linearize a directed acyclic graph (DAG). y g p ( ) Algorithm : Algorithm : • Run BFS search and colour all nodes in odd layers red, others blue • Go through all edges in adjacency list and check if each of them has two different B D A colours at its ends if so then G is bipartite, otherwise it is not colours at its ends - if so then G is bipartite, otherwise it is not We use the following alternative definitions in the analysis: • Graph G = (V,E) is bipartite iff all its cycles have even length, or • Graph G (V,E) is bipartite iff it has no odd cycle Graph G = (V E) is bipartite iff it has no odd cycle C C E E C A B D E bi bipartite tit non bipartite
Topological Sort p g Example p � Performed on a DAG. � Performed on a DAG. A B D � Linear ordering of the vertices of G such that if 1/ ( u , v ) ∈ E , then u appears before v . ( , ) , pp Topological-Sort ( G ) call DFS( G ) to compute finishing times f [ v ] for all v ∈ V 1. C 2. as each vertex is finished, insert it onto the front of a linked list E 3. return the linked list of vertices Linked List: Linked List: Time: Θ ( V + E ). Example p Example p A B A B D D 1/ 1/ 2/ 2/3 C C E E Linked List: Linked List: Linked List: Linked List: 2/3 E E
Example p Example p A B A B D D 1/4 5/ 1/4 2/3 2/3 C C E E Linked List: Linked List: Linked List: Linked List: 1/4 2/3 1/4 2/3 E E E E D D D D Example p Example p A B A B D D 5/ 5/ 1/4 1/4 6/ 2/3 6/7 2/3 C C E E Linked List: Linked List: Linked List: Linked List: 1/4 2/3 6/7 1/4 2/3 E E E E C C D D D D
Example p Example p A B A B D D 5/8 1/4 5/8 1/4 9/ 6/7 2/3 6/7 2/3 C C E E Linked List: Linked List: Linked List: Linked List: 6/7 1/4 2/3 6/7 1/4 2/3 5/8 5/8 E E E E B B C C D D B B C C D D Example p Precedence Example p � Tasks that have to be done to eat � Tasks that have to be done to eat A B D breakfast: 5/8 1/4 9/10 � get glass pour juice get bowl pour cereal � get glass, pour juice, get bowl, pour cereal, pour milk, get spoon, eat. 6/7 2/3 � Certain events must happen in a certain � Certain events must happen in a certain C E order (ex: get bowl before pouring milk) Linked List: Linked List: � For other events, it doesn't matter (ex: F th t it d 't tt ( get bowl and get spoon) 6/7 1/4 2/3 5/8 9/10 E E C C A A B B D D
Precedence Example p Precedence Example p � Topological Sort � Topological Sort get glass get bowl pour juice pour juice 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11 12 12 13 13 14 14 pour cereal eat milk spoon get spoon get spoon pour milk ilk juice cereal glass bowl eat breakfast consider reverse order of finishing times: spoon, bowl, cereal, milk, glass, juice, eat Order: glass, juice, bowl, cereal, milk, spoon, eat. Precedence Example p Correctness Proof � Show if ( u, v ) ∈ E , then f [ v ] < f [ u ]. � What if we started with juice? � What if we started with juice? � When we explore ( u, v ), what are their colors? � Note, u is gray – we are exploring it � Is v gray? g y 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11 12 12 13 13 14 14 � No , because then v would be an ancestor of u . � ⇒ ( u, v ) is a back edge. � ⇒ a cycle (dag has no back edges). eat milk glass spoon � Is v white? � Is v white? juice cereal � Then v becomes descendant of u . � By parenthesis theorem, d [ u ] < d [ v ] < f [ v ] < f [ u ]. bowl � Is v black? � Is v black? � Then v is already finished. consider reverse order of finishing times: � Since we’re exploring ( u, v ), we have not yet finished u . spoon, bowl, cereal, milk, glass, juice, eat � Therefore, f [ v ] < f [ u ].
Uses of SCC’s Strongly Connected Components � Packaging software modules � Packaging software modules � Consider a directed graph. � Consider a directed graph � Construct directed graph of which modules � A strongly connected component (SCC) call which other modules of the graph is a maximal set of nodes of the graph is a maximal set of nodes � A SCC is a set of mutually interacting with a (directed) path between every pair modules of nodes. of nodes � Pack together those in the same SCC � If a path from u to v exists in the SCC, then a path from v to u also exists a path from v to u also exists. � Problem: Find all the SCCs of the graph. SCC Example p Main Idea of SCC Algorithm g � DFS tells us which nodes are reachable � DFS tells us which nodes are reachable from the roots of the individual trees h f a e � Also need information in the other � Also need information in the other direction: is the root reachable from its g g c c b b d d descendants? descendants? � Run DFS again on the transpose graph (reverse the directions of the edges) ( th di ti f th d ) four SCCs
SCC Algorithm g SCC Algorithm Example g p Input: directed graph G = (V,E) Input: directed graph G = (V E) h f a e 1. call DFS(G) to compute finishing times 2. compute G T // transpose graph G T // t t h g c b d 3. call DFS(G T ), considering nodes in decreasing order of finishing times 4. each tree from Step 3 is a separate p p input graph - run DFS input graph run DFS SCC of G After Step 1 p After Step 2 p fin(c) fin(d) fin(b) fin(e) fin(a) fin(h) fin(g) fin(f) h f a e 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11 12 12 13 13 14 14 15 15 16 16 c d h g g c c b b d d b e g a f transposed input graph - run DFS with specified order of transposed input graph run DFS with specified order of nodes Order of nodes for Step 3: f, g, h, a, e, b, d, c
After Step 3 p Run Time of SCC Algorithm g � Step 1: O(V+E) to run DFS � Step 1: O(V+E) to run DFS � Step 2: O(V+E) to construct transpose graph assuming adjacency list rep graph, assuming adjacency list rep. 1 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10 10 11 11 12 12 13 13 14 14 15 15 16 16 � Adjacency matrix is O(1) time w/ wrapper. g � Step 3: O(V+E) to run DFS again S O( ) S h e c f � Step 4: O(V) to output result a b d � Total: O(V+E) SCCs are {f,h,g} and {a,e} and {b,c} and {d}. Component Graph p p Component Graph Facts p p � Claim: G SCC is a directed acyclic graph. � G SCC = ( V SCC E SCC ) y g p ( V � G , E ). � Suppose there is a cycle in G SCC such that � V SCC has one vertex for each SCC in G . component C i is reachable from component C j and vice versa. � E SCC has an edge if there’s an edge E SCC h d if th ’ d � Then C i and C j would not be separate SCCs. � Lemma: If there is an edge in G SCC from between the corresponding SCC’s in G . component C' to component C then component C to component C, then {a,e} { } f(C') > f(C). � Consider any component C during Step 1 (running {f,h,g} {d} {d} DFS on G) DFS on G) � Let d(C) be earliest discovery time of any node in C G SCC based on example {b,c} � Let f(C) be latest finishing time of any node in C graph from before graph from before
Recommend
More recommend
![Elementary Graph Algorithms [for graphs with no edge weights] Course: CS 5130 - Advanced Data](https://c.sambuz.com/1035513/elementary-graph-algorithms-s.jpg)
