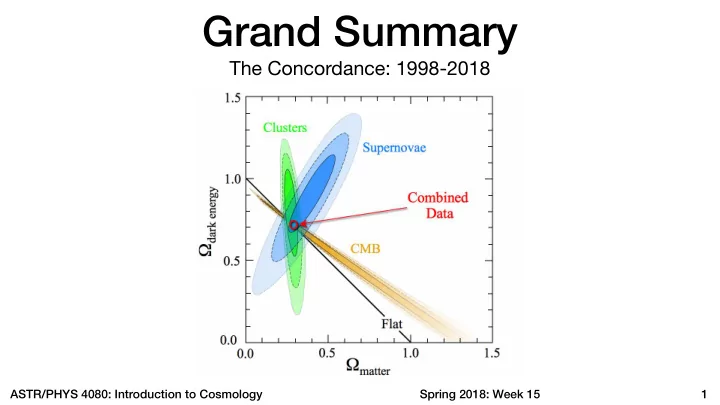
Grand Summary The Concordance: 1998-2018 ASTR/PHYS 4080: - PowerPoint PPT Presentation

Grand Summary The Concordance: 1998-2018 ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 1

Theory ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 2

Benchmark Model 2 Kt a ∝ e 0 log(a) 2/3 a ∝ t − 2 t 0 t m Λ − 4 1/2 a ∝ t t rm − 6 − 10 − 8 − 6 − 4 − 2 0 log(H 0 t) ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 3

Early Universe Timescales strong force freeze out weak force freeze out ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 4

Early Universe (Fundamental) Scales ◆ 1 / 2 ✓ G ~ Planck time: = 5 . 4 × 10 − 44 s t p ≡ c 5 ◆ 1 / 2 ✓ G ~ Planck length: = 1 . 6 × 10 − 33 cm l p ≡ c 3 ◆ 1 / 2 ✓ ~ c Planck mass: = 2 . 2 × 10 − 5 g M p ≡ G ◆ 1 / 2 ✓ ~ c 5 E p = M p c 2 = Planck energy: = 1 . 2 × 10 28 eV = 1 . 2 × 10 19 GeV G Planck temperature: T p = E p /k = 1 . 4 × 10 32 K Planck units: c = k = ~ = G = 1 ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 5

ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 6

Key Relations ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 7

ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 8

ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 9

Curvature How can we measure the curvature of spacetime? = area of triangle = Radius of Curvature Only possible geometries that are homogeneous/isotropic ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 10

Lengths of Geodesics (3D, polar coords) straight lines in a given geometry <OR> flat or Euclidean space: elliptical or spherical space: hyperbolic space: ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 11

Minkowski & Robertson-Walker Metrics metrics define the distance between events in spacetime Minkowski (no gravity: metric in SR) Robertson-Walker (with gravity, if spacetime is homogeneous & isotropic) { light travels along cosmological proper null geodesics, i.e.: time or cosmic time comoving coordinates ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 12

Only 1 Constituent in a Flat Spacetime ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 13

Matter + Lambda + Curvature ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 14

Inflation - quark soup - neutron capture - nucleosynthesis - recomb/decoup kT: 150 MeV 10 MeV 0.07 MeV 3760/2970K baryogenesis photon-baryon ratio Early Universe Timescales ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 15

neutron-proton ratio ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 16

Nuclear Binding Energy release energy expect nucleosynthesis to result in all atoms becoming iron does not happen - why not? ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 17

BBN ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 18

Recombination (minus for bosons, plus for fermions) g —> 2 (for non-nucleons, g H =4) chemical potential of photons = 0 Saha Equation ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 19

Surface of Last Scattering ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 20

Reionization ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 21

Observation ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 22

Olber’s Paradox (1823) Resolution? ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 23

Cosmological Principle The universe is isotropic on very large scales. (>100Mpc). Copernican Principle => homogeneous & isotropic (Cosmological Principle) Radio sources from NVSS (Condon et al. 2003) ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 24

Near perfect BB everywhere on the sky dT/T ~ 10 -3 ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 25

Abundances from Nucleosynthesis Creation process depends on relative abundances at any given time, so have to calculate computationally Nucleosynthesis doesn’t run to completion like in stars — rapidly dropping temperature cuts it off and “freezes” abundance pattern Exact yields depend most on baryon- to-photon ratio: (determines temperature of nucleosynthesis) ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 26

Practical Distance Measures Luminosity Distance Angular Diameter Distance ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 27

Practical Distance Measures ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 28

How distances are affected by underlying cosmology Luminosity Distance Angular Diameter Distance ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 29

Practical Distance Measures ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 30

Getting distances to the nebulae 1000 km/s 2 Mpc ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 31

Practical Distance Measures ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 32

ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 33

CMB provides a giant triangle of known size! ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 34

Acoustic peaks causal contact initial conditions first peak second peak third peak etc peaks size scale of a DM potential well where baryon collapse reaches turnaround due to its pressure ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 35

Baryonic Matter By the time of the Big Bang and thereafter, normal matter is the subdominant form of matter in the universe, with some other form of matter (non-baryonic dark matter) making up the majority of non-relativistic matter in the universe Could be primordial black holes that were made before this time (i.e., not from stars). ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 36

Dark Matter in Galaxies ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 37

Detecting MACHOs via gravitational lensing b b d xd d b ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 38

Temperature of the Dark Matter Hot Warm Cold velocity of particles compared to the speed of light relativistic at time of collapse (like neutrinos): hot non-relativistic at time of collapse (like WIMPs): cold fast motions wipe out initial overdensities on small scales: “free-streaming” ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 39

Power spectrum of density fluctuations Power spectrum defined to be the mean squared amplitude of the Fourier components: Gaussian field: each component uncorrelated and random, drawn from the Gaussian distribution Inflation predicts this (random quantum fluctuations) and a power law power spectrum (with n=1) ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 40

Acoustic peaks First peak: causal contact initial spatially flat conditions first peak Second peak: existence of “dark baryons” second peak third peak Third peak: amount of dark matter etc peaks Damping tail: damping tail photons can cross entire grav. fluct., wipes out signal ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 41

Baryon Acoustic Oscillations To measure, use galaxies to trace the signature of these oscillations The number of galaxies should be correlated with each other on scales comparable to the sound horizon of the largest acoustic peaks (~150 Mpc comoving) The number of galaxies within a given volume is Eisenstein+ 2005 ASTR/PHYS 4080: Introduction to Cosmology Spring 2018: Week 15 � 42