Finding a Needle in the Haystack of Hardened Interconnect Patterns - PowerPoint PPT Presentation

Finding a Needle in the Haystack of Hardened Interconnect Patterns S. Nikolić, G. Zgheib*, and P. Ienne FPL19, Barcelona, 09.09.2019 École Polytechnique Fédérale de Lausanne *Intel Corporation

Why harden connections? 2 crossbar LUT LUT LUT

Why harden connections? 2 crossbar LUT LUT LUT

Why harden connections? 2 crossbar LUT LUT LUT

Why harden connections? 2 crossbar LUT LUT LUT

Why harden connections? 2 crossbar LUT LUT LUT

Why harden connections? 2 crossbar LUT LUT LUT

Why harden connections? 2 crossbar LUT LUT LUT

What is the price? 3 crossbar LUT LUT LUT Circuit to be mapped Cluster architecture

XC4000 [1] UTFPGA1 [2] Triptych [3] [1] H.-C. Hsieh, W. S. Carter, J. Ja, E. Cheung, S. Schreifels, C. Erickson, P. Freidin, L. Tinkey, and R. Kanazawa. Third-generation architecture boosts speed and density of fi eld-programmable gate arrays, 1990 [2] P. Chow, S. O. Seo, D. Au, B. Fallah, C. Li, and J. Rose. A 1.2um CMOS FPGA using cascaded logic blocks and segmented routing, 1991 [3] C. Ebeling, G. Borriello, S. A. Hauck, D. Song, E. A. Walkup. TRIPTYCH: A New FPGA Architecture, 1991

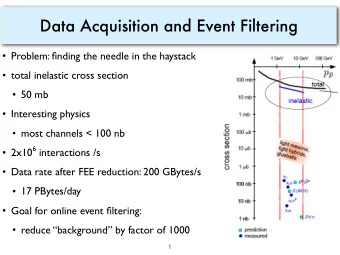
5 � 5-LUT � 10 8 Challenges How to design the patterns? • Intuition? • Enumeration How to map on patterns? (CAD tool scalability) 5 12 LUT LUT LUT LUT LUT

5 � 5-LUT � 10 8 Challenges How to design the patterns? • Intuition? • Enumeration How to map on patterns? (CAD tool scalability) 5 12 LUT LUT LUT LUT LUT

5 � 5-LUT � 10 8 Challenges How to design the patterns? • Intuition? • Enumeration How to map on patterns? (CAD tool scalability) 5 12 LUT LUT LUT LUT LUT

5 � 5-LUT � 10 8 Challenges How to design the patterns? • Intuition? • Enumeration How to map on patterns? (CAD tool scalability) 5 12 LUT LUT LUT LUT LUT

Challenges How to design the patterns? • Intuition? • Enumeration How to map on patterns? (CAD tool scalability) 5 12 5 � 5-LUT � 10 8 LUT LUT LUT LUT LUT

Enumeration

Representation • represent each LUT by a node (circles) • only represent shared inputs (triangles) • each edge is a hardened connection 6 I I LUT LUT LUT LUT LUT LUT

Representation • represent each LUT by a node (circles) • only represent shared inputs (triangles) • each edge is a hardened connection 6 I I LUT LUT LUT LUT LUT LUT

Representation • represent each LUT by a node (circles) • only represent shared inputs (triangles) • each edge is a hardened connection 6 I I LUT LUT LUT LUT LUT LUT

Representation • represent each LUT by a node (circles) • only represent shared inputs (triangles) • each edge is a hardened connection 6 I I LUT LUT LUT LUT LUT LUT

Representation • represent each LUT by a node (circles) • only represent shared inputs (triangles) • each edge is a hardened connection 6 I I LUT LUT LUT LUT LUT LUT

Enumeration (no input sharing for now) 7 a c b //V - vertex set G = (V, {}) expandable = (G) while expandable { G = pop(expandable) for e in V x V { if keep(G + e) { push(G + e, expandable) } } }

Enumeration (no input sharing for now) 7 a c b //V - vertex set G = (V, {}) expandable = (G) a c b a c b while expandable { G = pop(expandable) for e in V x V { if keep(G + e) { push(G + e, expandable) } } }

Enumeration (no input sharing for now) 7 a c b //V - vertex set G = (V, {}) expandable = (G) a c b a c b while expandable { G = pop(expandable) for e in V x V { a c a c b b a c b a c if keep(G + e) { b push(G + e, expandable) } } }

Enumeration (no input sharing for now) 7 a c b //V - vertex set G = (V, {}) expandable = (G) a c b a c b while expandable { G = pop(expandable) for e in V x V { a c a c b b a c b a c if keep(G + e) { keep b push(G + e, expandable) } } }

When to stop? When area or delay stop decreasing? When area or delay start increasing? 8

When to stop? When area or delay stop decreasing? When area or delay start increasing? 8

When to stop? 9 Circuit to be mapped No hardened connections 7 LUT LUT LUT

9 When to stop? Circuit to be mapped With hardened connections 7 No hardened connections LUT LUT LUT 7 LUT LUT LUT

9 When to stop? Circuit to be mapped With hardened connections 7 No hardened connections LUT LUT LUT 7 LUT LUT LUT

When to stop? 9 Circuit to be mapped With hardened connections 7 No hardened connections LUT LUT LUT 7 7 LUT LUT LUT LUT LUT LUT

When to stop? 9 Circuit to be mapped With hardened connections 7 No hardened connections LUT LUT LUT 7 7 LUT LUT LUT LUT LUT LUT When area or delay stop decreasing? When area or delay start increasing?

When to stop?

Other issues: avoiding listing duplicates 11 A A B C B C

Other issues: maintaining subgraph relations 12 x y z xx xy xz yy yz zz xxx xxy xxz xyy xyz xzz yyy yyz yzz zzz G H 1 H 2

Challenges How to design the patterns? • Intuition? • Enumeration How to map on patterns? (CAD tool scalability) 13 12 5 � 5-LUT � 10 8 LUT LUT LUT LUT LUT

Experiments

( � 10 8 patterns) Setup • Search space: acyclic five 5-LUT patterns • Architecture = 4x the pattern with a shared crossbar (20 5-LUT clusters) 14

Setup • Search space: acyclic five 5-LUT patterns • Architecture = 4x the pattern with a shared crossbar (20 5-LUT clusters) 14 ( � 10 8 patterns)

Setup • Search space: acyclic five 5-LUT patterns • Architecture = 4x the pattern with a shared crossbar (20 5-LUT clusters) 14 ( � 10 8 patterns)

Results Found 261 patterns with only 12 external inputs achieving 15 Some examples a e d b e b a c c d 12 b e a d e a c b d c � 80 % packing density

Results 16 95 90 85 utilization [%] 80 75 70 65 blob_merge boundtop ch_intrinsics mkDelayWorker32B diffeq1 diffeq2 mkPktMerge mkSMAdapter4B or1200 raygentop stereovision0 sha stereovision1 stereovision3

Conclusions Numerical results not satisfactory (18-29% critical path delay increase) But... We have an efficient way of searching for good patterns • search techniques completely independent of the mapping algorithms In the future, this should help us understand what makes a good pattern and profit from connection hardening to the fullest 17 • searched the space � 10 8 in < 12h

Thank you for attention For questions, please see the poster