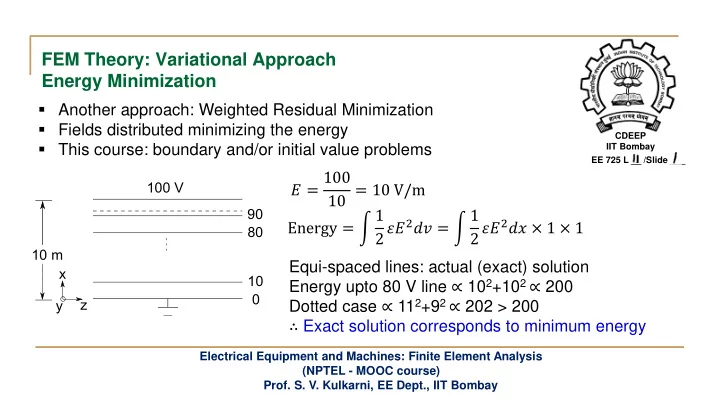
FEM Theory: Variational Approach Energy Minimization Another - PowerPoint PPT Presentation

FEM Theory: Variational Approach Energy Minimization ▪ Another approach: Weighted Residual Minimization ▪ Fields distributed minimizing the energy CDEEP ▪ This course: boundary and/or initial value problems IIT Bombay EE 725 L __ /Slide ___ 𝐹 = 100 10 = 10 V/m Energy = න 1 2 𝜁𝐹 2 𝑒𝑤 = න 1 2 𝜁𝐹 2 𝑒𝑦 × 1 × 1 Equi-spaced lines: actual (exact) solution Energy upto 80 V line ∝ 10 2 +10 2 ∝ 200 Dotted case ∝ 11 2 +9 2 ∝ 202 > 200 ∴ Exact solution corresponds to minimum energy Electrical Equipment and Machines: Finite Element Analysis (NPTEL - MOOC course) Prof. S. V. Kulkarni, EE Dept., IIT Bombay

Source free electrostatic proble : charges on plates → boundar voltage Energ = න 1 2 𝜁𝐹 2 𝑒𝑤 PDEs in Electromagnetics Magnetostatic: 𝛂 2 𝐁 = −𝜈 CDEEP J IIT Bombay EE 725 L __ /Slide ___ Transient: 𝛂 2 𝐁 − 𝜈𝜏 𝜖𝐁 Time harmonic ⇒ 𝛂 2 𝐁 − 𝑘𝜕𝜈𝜏𝐁 = −𝜈 𝜖𝑢 = −𝜈 J J 2 Mini i ation of න 1 2 𝜁𝐹 2 𝑒𝑤 ⇒ න 1 2 𝜁 𝜖𝑊 𝑒𝑦 × 1 × 1 for 1-D Electrostatics 𝜖𝑦 𝑄 2 𝑔 𝑦, 𝜚, 𝜚 ′ 𝑒𝑦 𝐺(𝜚) = න 𝜚(𝑄 1 ) = 𝜚 1 , 𝜚(𝑄 2 ) = 𝜚 2 Define functional 𝑄 1 Laplace Eq: only 𝜚 ′ appears in F Independent variable: 𝑦 Poisson’s Eq: 𝜚 also appears Dependent variable: 𝜚 Electrical Equipment and Machines: Finite Element Analysis (NPTEL - MOOC course) Prof. S. V. Kulkarni, EE Dept., IIT Bombay

𝑒𝐺 = 𝜖𝐺 𝜖𝑦 𝑒𝑦 + 𝜖𝐺 𝜖𝜚 𝑒𝜚 + 𝜖𝐺 𝜖𝜚 ′ 𝑒𝜚 ′ 𝜀𝜚→ g ( 𝑦 ) 𝜖𝜚 𝜀𝜚 + 𝜖𝐺 𝜖𝐺 𝜖𝜚 ′ 𝜀𝜚 ′ 𝜀𝐺 = 𝜀𝑦 = 0 CDEEP IIT Bombay 𝜀𝜚 → variation in 𝜚 at (fixed) 𝑦 EE 725 L __ /Slide ___ ⇒ 𝑦  𝜚 → g ( 𝑦 ) 𝜀𝑦 = 0 𝜀𝐺 = 𝐺(𝜚 + 𝜀𝜚) − 𝐺(𝜚) = 0 → gives solution 𝑄 2 𝑄 2 𝑔 𝑦 + 𝜀𝑦, 𝜚 + 𝜀𝜚, 𝜚 ′ + 𝜀𝜚 ′ 𝑒𝑦 − න 𝑔 𝑦, 𝜚, 𝜚 ′ 𝑒𝑦 = 0 = න 𝑄 1 𝑄 1 0 𝑕 𝑕′ Ref: M. N. O. Sadiku, Numerical Techniques in Electromagnetics, CRC Press, 3 rd Edition, 2009 Electrical Equipment and Machines: Finite Element Analysis (NPTEL - MOOC course) Prof. S. V. Kulkarni, EE Dept., IIT Bombay

Using Taylor series expansion and considering only 1 st order terms න 𝑔(𝑦, 𝜚, 𝜚′)𝑒𝑦 + න 𝑕 𝜖𝑔(𝑦, 𝜚, 𝜚′) + 𝑕 ′ 𝜖𝑔(𝑦, 𝜚, 𝜚′) 𝑒𝑦 − න𝑔(𝑦, 𝜚, 𝜚′)𝑒𝑦 = 0 𝜖𝜚 ′ 𝜖𝜚 𝑄 2 න 𝜖𝑔 𝜖𝑔 − න 𝑕 𝑒 𝜖𝑔 CDEEP 𝜖𝜚 𝑕𝑒𝑦 + 𝜖𝜚 ′ 𝑕 𝜖𝜚 ′ 𝑒𝑦 = 0 IIT Bombay 𝑒𝑦 EE 725 L __ /Slide ___ 𝑄 1 𝜀𝜚 𝑄 2 ⇒ න 𝜖𝑔 𝜖𝜚 − 𝑒 𝜖𝑔 𝜖𝑔 𝑕𝑒𝑦 + 𝜖𝜚 ′ 𝑕 = 0 𝜖𝜚 ′ 𝑒𝑦 𝑄 1  න 𝜖𝑔 𝜖𝜚 − 𝑒 𝜖𝑔 ∵ 𝑕 = 0 at boundary points 𝑕𝑒𝑦 = 0 ( ∵ potentials fixed) 𝜖𝜚 ′ 𝑒𝑦 ⇒ 𝜖𝑔 𝜖𝜚 − 𝑒 𝜖𝑔 Function 𝑔 must satisfy Euler-Lagrange = 0 ⇒ 𝜀𝐺 = 0 𝜖𝜚 ′ 𝑒𝑦 (E-L) Eq to minimize the functional F Electrical Equipment and Machines: Finite Element Analysis (NPTEL - MOOC course) Prof. S. V. Kulkarni, EE Dept., IIT Bombay

Parallel Plate Capacitor Problem 2 2 𝐺 = 1 2 න 𝜁𝐹 2 𝑒𝑦 × 1 × 1 = 1 2 𝜁 න 𝑒𝑊 𝑒𝑦 ⇒ 𝑔 = 1 2 𝜁 𝑒𝑊 𝑒𝑦 𝑒𝑦 CDEEP Substituting 𝑔 in E-L equation: IIT Bombay EE 725 L __ /Slide ___ ⇒ 0 − 𝑒 𝜖 1 2 𝜁 𝑊 ′ 2 = 0 𝜖𝑊 ′ 𝑒𝑦 𝜖𝑦 2𝑊 ′ = 0 ⇒ 𝑒 2 𝑊 − 1 2 𝜁 𝜖 Laplace equation in −D 𝑒𝑦 2 = 0 𝑔 : function of 𝑊′ here but in general of 𝑦, 𝑊, 𝑊′ Electrical Equipment and Machines: Finite Element Analysis (NPTEL - MOOC course) Prof. S. V. Kulkarni, EE Dept., IIT Bombay