
Lecture 14: Anharmonic Oscillator and Raman Effect
Transition Moment Integral • Can be evaluated analytically • Often simplified by symmetry • Gives rise to selection rules if recursion formulae exist
The chemical bond as a simple harmonic oscillator ( ) = 1 Parabolic potential: V x 2 kx 2 Schrödinger equation: Boundary condition: = 0 at x = + ∞ E v = ( v + ½) ħω SHO: a good approximation for small displacements
The chemical bond as a simple harmonic oscillator v = Vibrational quantum number = 0, 1, 2, 3, … k Force constant w = m Reduced mass E v+1 – E v = = h /2 = h n k k 1 n = 1 n = 2 p c m 2 p m E v=0 = ½ ħω Zero point energy
Spectrum of a harmonic oscillator v = Vibrational quantum number = 0, 1, 2, 3, … Intensity k Force constant w = D v =1 m Reduced mass E v+1 – E v = = h /2 = h n 2000 3000 0 1000 Energy of transition k IR Spectrum: k 1 n = 1 n = Bond strength 2 p c m 2 p m Polyatomic molecule: Different Bond strengths Functional groups
High resolution IR spectrum of HCl Rotational fine structure D v =1, D J =+1 Isotope effect
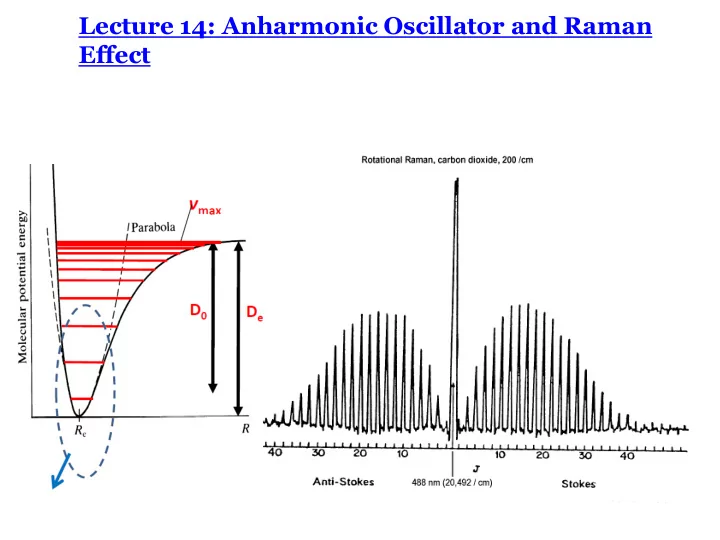
Anharmonic oscillator • The bond breaks at large displacements Morse potential • Bond dissociation energy SHO: a good approximation only for small displacements
Anharmonic oscillator • The bond breaks at large displacements Morse potential • Bond dissociation energy • Energy levels come closer for higher values of v • Fundamental and overtones in IR spectra SHO: a good approximation only for small displacements
Anharmonic oscillator: Energies • The bond breaks at large displacements Morse potential • Bond dissociation energy • Energy levels come closer for higher values of v • Fundamental and overtones in IR spectra e v = ( v + ½) n - ( v + ½) 2 x e n x e = n/ 4 D e D v =+1, +2, + 3,…. SHO: a good approximation only for small displacements
Anharmonic oscillator: “Selection” rules • The bond breaks at large displacements Morse potential • Bond dissociation energy • Energy levels come closer for higher values of v • Fundamental and overtones in IR spectra e v = ( v + ½) n - ( v + ½) 2 x e n x e = n/ 4 D e D v =+1, +2, + 3,…. Fundamental 1 st Overtone 2 nd Overtone
Anharmonic oscillator: Position of spectral lines e 0 = 1 n - 1 x e n 2 4 e 1 = 3 2 n - 9 4 x e n e 2 = 5 n - 25 x e n e v = ( v + ½) n - ( v + ½) 2 x e n 2 4 e 3 = 7 n - 49 x e n x e = n/ 4 D e 2 4 D v =+1, +2, + 3,…. Fundamental 1 st Overtone 2 nd Overtone
Anharmonic oscillator: Position of spectral lines e 1 - e 0 = n - 2 x e n = n (1 - 2 x e ) e 0 = 1 n - 1 x e n 2 4 e 2 - e 0 = 2 n - 6 x e n = 2 n (1 - 3 x e ) e 1 = 3 2 n - 9 4 x e n e 3 - e 0 = 3 n - 12 x e n = 3 n (1 - 4 x e ) e 2 = 5 n - 25 x e n 2 4 e 3 = 7 n - 49 x e n x e = n/ 4 D e 2 4 D v =+1, +2, + 3,…. Fundamental 1 st Overtone 2 nd Overtone
Anharmonic oscillator: Position of spectral lines e 1 - e 0 = n - 2 x e n = n (1 - 2 x e ) e 0 = 1 n - 1 x e n 2 4 e 2 - e 0 = 2 n - 6 x e n = 2 n (1 - 3 x e ) e 1 = 3 2 n - 9 4 x e n e 3 - e 0 = 3 n - 12 x e n = 3 n (1 - 4 x e ) e 2 = 5 n - 25 x e n Intensity 2 4 e 3 = 7 n - 49 x e n 2 4 Wavenumber x e = n/ 4 D e Fundamental D v =+1, +2, + 3,…. 1 st Overtone 2 nd Overtone
IR Spectrum of Carbon Monoxide Fundamental Peak 2143 cm -1 First Overtone 4260 cm -1
IR Spectrum of Carbon Monoxide: High resolution Fundamental Peak 2143 cm -1 First Overtone 4260 cm -1
Population of states and hot band Morse potential Boltzmann distribution: ( ) n µ exp -e v / kT v Typical energy gap: 100s and 1000s of cm -1 n = 0.008 v = 1 n v = 0 Hot band for energy gap of 1000 cm -1 High temperature: v =1 to v = 2 ….. are possible Intensity of hot band: Population of v =1 at that temperature
How to find out bond length of H 2 ? Diatomic molecule, NO permanent dipole moment • Polarizability: Induced dipole moment. • Molecular rotation or vibration: Oscillating induced dipole Raman Spectroscopy Scattering of (usually) visible monochromatic light by • molecules of a gas, liquid or solid Two kinds of scattering : • – Rayleigh (1 in every 10,000) : No change in frequency – Raman (1 in every 10,000,000): Change in frequency
Raman Spectroscopy Virtual level Anti- n ex n Stokes Stokes shift shift 0 Dn ( = n n ex ) Dn : energy gaps in molecule • Rayleigh scattering: no change in energy of light Dn : No dpendence on n ex • Raman scattering: Stokes strong, anti-Stokes • different from original weak for vibrational levels
Rotational Raman Spectroscopy: CO 2 D = Selection Rule: 0, 2 J
CH 107 in a nutshell: Quantum mechanics in Chemistry: Theory and its manifestations ˆ H y = E y
CH 107 in a nutshell: Bold thoughts from great minds
CH 107 in a nutshell: Don’t be a frog in the well. “Seek, and ye shall find” history.cultural-china.com vkaisthaaseem.blogspot.com
All the best for all that you do in future
Recommend
More recommend