Directed Graphs y = f(x) y (Digraphs) x Albert R Meyer March - PowerPoint PPT Presentation

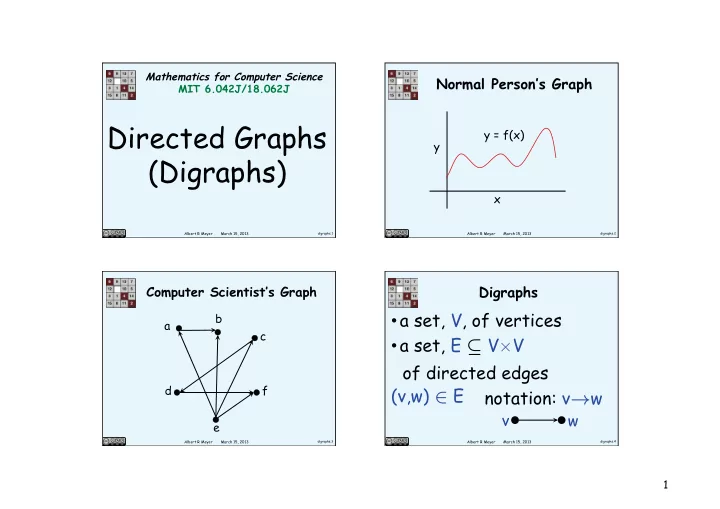
Mathematics for Computer Science Normal Person’s Graph MIT 6.042J/18.062J Directed Graphs y = f(x) y (Digraphs) x Albert R Meyer March 15, 2013 digraphs.1 Albert R Meyer March 15, 2013 digraphs.2 Computer Scientist’s Graph Digraphs • a set, V, of vertices b a c • a set, E ⊆ V × V of directed edges d f (v,w) ∈ E notation: v → w v w e Albert R Meyer March 15, 2013 digraphs.3 Albert R Meyer March 15, 2013 digraphs.4 1

Relations and Graphs Digraphs a b Formally, a digraph with vertices V is d c the same as a binary V= {a,b,c,d} relation on V. E = {(a,b), (a,c), (c,b)} Albert R Meyer March 15, 2013 digraphs.5 Albert R Meyer March 15, 2013 digraphs.6 Walks & Paths Walks & Paths Path: walk thru vertices Walk: follow successive edges without repeat vertex length: 5 edges length: 4 edges stuck! (not the 6 vertices) Albert R Meyer March 15, 2013 Albert R Meyer March 15, 2013 digraphs.7 digraphs.8 2

Matrix representation Matrix representation • • • • • • • • • • • •         1   •  •            •     •               •  •                •  •              •  •                   •   •       Albert R Meyer March 15, 2013 Albert R Meyer March 15, 2013 digraphs.9 digraphs.10 Matrix representation Adjacency Matrix • • • • • • • • • • • •        •  1 1 1 1  •            •       •     1 1      •              •  1 •                 •   •     1       •        •    1       •     1  Albert R Meyer March 15, 2013 Albert R Meyer March 15, 2013 digraphs.12 digraphs.11 3

Adjacency Matrix • • • • • •    0  1 0 0 0 1  •       •  0 0 1 0 1 0         •  0 0 0 1 0 0        •  0  1 0 0 0 0      •    0 0 0 0 0 1       •     0 1 0 0 0 0  Albert R Meyer March 15, 2013 digraphs.14 4

MIT OpenCourseWare http://ocw.mit.edu 6.042J / 18.062J Mathematics for Computer Science Spring 20 15 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.