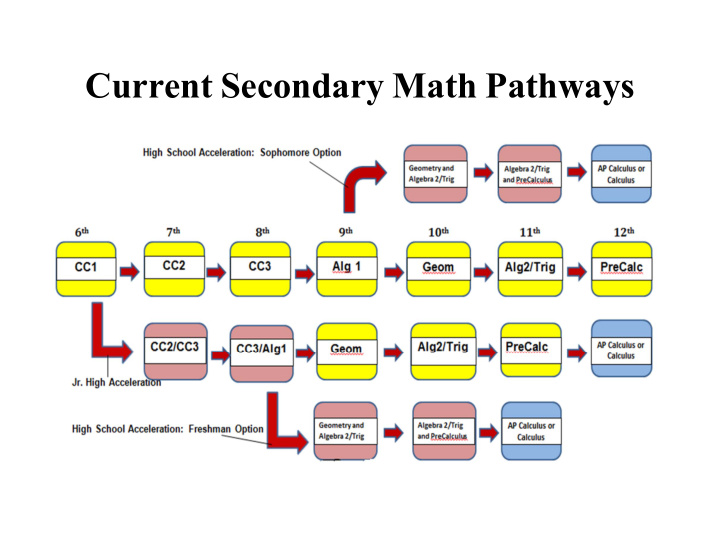



Current Secondary Math Pathways
UC Qualified with No Acceleration
Junior High Pathways Regular Pathway
Options for Junior High Accelerated Students in High School 9th 10th 11 th 12th 1. Move to non ‐ accelerated pathway 2. Move to high school accelerated pathway Criteria: B ‐ or higher for both semesters of 8th
Entering Accelerated Pathway in 10 th Grade Criteria: Grade of “A” for both semesters and 90% or above on all district benchmarks.
Proposed Modifications • Name Change: CC3 changed to Foundational Algebra and Geometry to reflect course content • Offer Summer Bridge Class to high performing 7 th grade students to allow students to enter accelerated pathway in 8 th grade – Criteria: Grade of “A” at both semesters and 90% or higher on district benchmarks
Proposed Modifications • Allow students on non ‐ accelerated pathway to take Algebra 2 or Algebra 2/Trig as an elective
Major Topics 6 th Grade: Foundations for the 7 th Grade Transition to Algebraic Representation • Properties of Rational • Integers and their Numbers operations • Expressions and Linear • Fluency in Division of Equations Fractions • Rate and Problem Solving • Ratios, proportional using Rate reasoning, problem solving • Proportional Reasoning • Expressions, Equations, and • Algebraic Modeling with Inequalities Equations • Geometry ‐ area, surface • Geometry: Angles, 3D area, volume Shapes • Statistics • Statistics and Probability
Major Topics 8 th Grade • Equations • Introduction to Systems • Introduction to Functions • Graphing • Rational/Irrational Numbers • Exponents • Pythagorean Theorem • Geometry: – Rotations, Reflections, and Translations – Triangle Proofs – Volume of 3D objects • Bivariate Data
Recommend
More recommend