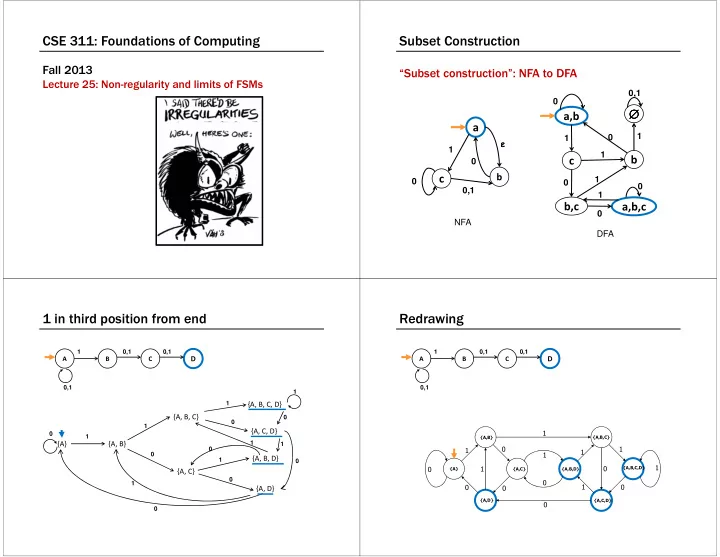
CSE 311: Foundations of Computing Subset Construction Fall 2013 - PowerPoint PPT Presentation

CSE 311: Foundations of Computing Subset Construction Fall 2013 “Subset construction”: NFA to DFA Lecture 25: Non-regularity and limits of FSMs 0,1 0 ∅ ∅ ∅ ∅ a,b a 1 0 1 ɛ ɛ ɛ ɛ 1 1 b c 0 b c 1 0 0 0 0,1 1 b,c a,b,c 0 NFA DFA 1 in third position from end Redrawing 1 0,1 0,1 1 0,1 0,1 D D A B C A B C 0,1 0,1 1 1 {A, B, C, D} {A, B, C} 0 0 1 {A, C, D} 1 0 1 {A,B} {A,B,C} {A} {A, B} 1 1 0 1 1 0 1 1 0 {A, B, D} 1 0 1 1 0 0 {A,B,C,D} {A} {A,C} {A,B,D} {A, C} 0 0 1 1 0 0 0 {A, D} {A,D} {A,C,D} 0 0

DFAs ≡ Regular expressions Languages and Machines! All We have shown how to build an optimal DFA for every regular expression – Build NFA – Convert NFA to DFA using subset construction Context-Free – Minimize resulting DFA Regular DFA Theorem: A language is recognized by a DFA if and 0* NFA Regex only if it has a regular expression Finite We show the other direction of the proof at the end {001, 10, 12} of these lecture slides Languages and Machines! DFAs Recognize Any Finite Language All Context-Free Warmup: Warmup: Warmup: Warmup: All finite Regular DFA languages 0* NFA are regular. Regex Finite {001, 10, 12}

Languages and Machines! An Interesting Infinite Regular Language All L = {x x ∊ x x ∊ { ∊ ∊ { 0, 1 } { { } } } * * * * : : : : x x x x has an equal number of substrings 01 and 10}. L is infinite. Context-Free Warmup 2: Warmup 2: Warmup 2: Warmup 2: Surprising Regular L is regular. DFA example here 0* NFA Regex Finite {001, 10, 12} Languages and Machines! Irregular Language! All B = {binary palindromes} can’t be recognized by any DFA Why is this language not regular? Context-Free Intuition (NOT A PROOF!): Main Event: Main Event: Main Event: Main Event: ??? Q: What would a DFA need to keep track of to decide the Q Q Q Prove there is Regular DFA language? a context-free 0* NFA A: It would need to keep track of the “first part” of the input A A A language Regex in order to check the second part against it that isn’t Finite …but there are an infinite # of possible first parts and we regular. only have finitely many states. {001, 10, 12} How do we prove it?

B = {binary palindromes} can’t be recognized by any DFA B = {binary palindromes} can’t be recognized by any DFA Consider the infinite set of strings Consider the infinite set of strings S={1, 01, 001, 0001, 00001, ...} = {0 n 1 : n ≥ 0} S={1, 01, 001, 0001, 00001, ...} = {0 n 1 : n ≥ 0} Suppose we are given an arbitrary DFA M M. M M • Goal: Show that some x x ∈ B B and some y y ∉ B B both must end x x B B y y B B That’s a nice set of first parts to have to remember but how up at the same state of M M M M can we argue that a DFA does the wrong thing for B? Since S S is infinite we know that two different strings in S S S S must S S x ∈ B and some y ∉ B both must end up • Show that some x x x land in the same state of M M M M, call them 0 0 0 0 i 1 1 1 and 0 1 0 0 j 0 j j j 1 1 1 1 for i≠j. at the same state of the DFA 0 i 1 ? 0 j 1 That state can’t be • That also must be true for 0 0 0 i 1z 0 1z and 0 1z 1z 0 0 j 1z 0 1z 1z 1z for any z z z z ∈ {0 0,1 0 0 1 1 1} * ! ! ! ! 0 i we get that 0 10 i and 0 10 i end up at the • a final state since then y is accepted: error on y In particular, with z z=0 z z 0 0 0 0 0 i 10 10 10 0 0 j 10 0 10 10 10 i ∈ B 10 i ∉ B same state of M M M. Since 0 M 0 i 10 0 0 10 10 B B and 0 B 0 0 0 j 10 10 10 B B (because i≠j) B • a non-final state since then x is rejected: error on x B. ∴ no DFA can recognize B M does not recognize B B B B B B. A={ 0 � 1 � ∶ � ≥ 0 } cannot be recognized by any DFA Showing a Language L is not regular 1. Find an infinite set S S S S={s s s s 0 0 ,s s 1 s s 1 ,...,s s s n s n ,...} of string prefixes that you 0 0 1 1 n n think will need to be remembered separately 2. “Let M M be an arbitrary DFA. Since S S is infinite and M M is finite M M S S M M state there must be two strings s s s s i i and s s j s s j in S S S S for some i i i i ≠j j j that j i i j j end up at the same state of M M.” M M Note: You don’t get to choose which two strings s s i i and s s j s s s s i i j j j 3. Find a string t t t (typically depending on s t s s s i i and/or s s s j s j ) such that i i j j s i s s s i t t t t is in L L, and or L L s s s s i i t t is not in L t t L L L , and i i i i s j s j t t is not in L L s s j j t t is in L L s s t t L L s s t t L L j j j j 4. “Since s s s i s i and s s s j s j both end up at the same state of M M M M, and we i i j j appended the same string t t t, both s t s s s i i t t and s t t s s s j j t t t end at the same t i i j j state of M. M. M. Since s M. s s i s i t t t ∈ L t L L L and s s j s s j t t t t ∉ L, L, L, L, M M does not recognize L M M L.” L L i i j j 5. “Since M M M M was arbitrary, no DFA recognizes L L L L.”

Another Irregular Language Example DFAs ≡ Regular expressions L = {x x x ∊ x ∊ ∊ ∊ { { { { 0, 1,2 } } } } * * * * : : x : : x x has an equal number of substrings 01 and 10}. x Intuition: Need to remember difference in # of 01 01 or 10 10 substrings 01 01 10 10 seen, but only hard to do if these are separated by 2 2 2 2’s. Theorem: A language is recognized by a DFA if and 1. Let S S S S={ ε , 012, 012012, 012012012, ...} = {(012) n : n ∊ ℕ } only if it has a regular expression 2. Let M M M M be an arbitrary DFA. Since S S S S is infinite and M M M M is finite state i and (012) j j for some i ≠ j that end there must be two strings (012) i i i j j Proof: Last class: RegExp → NFA → DFA up at the same state of M M. M M i to each of these strings. t = (102) i i i to each of these strings. to each of these strings. to each of these strings. 3. Consider appending string t t t i (102) i i ∈ j (102) i i ∉ Then (012) i i i i i ∈ L ∈ ∈ L but (012) j j j i i ∉ ∉ ∉ L L L L L since i ≠ j L Now: NFA → RegExp i (102) i i and (012) j j (102) i i end up at the same state of M 4. So (012) i i i i i j j i i M M M Enough since every DFA is also an NFA. i and (012) j j do. Since (012) i i (102) i i ∈ since (012) i i i j j i i i i ∈ L ∈ ∈ L and L L j (102) i i ∉ (012) j j j i i ∉ L ∉ ∉ L L, M L M M does not recognize L M L. L L 5. Since M M was arbitrary, no DFA recognizes L M M L L. L Generalized NFAs Starting from an NFA • Like NFAs but allow Add new start state and final state – Parallel edges ɛ ɛ ɛ ɛ – Regular Expressions as edge labels ɛ ɛ ɛ ɛ NFAs already have edges labeled ɛ ɛ ɛ or a ɛ ɛ ɛ ɛ ɛ • An edge labeled by A A can be followed by reading a A A string of input chars that is in the language Then eliminate original states one by one, represented by A A A A keeping the same language, until it looks • A string x is accepted iff there is a path from start like: to final state labeled by a regular expression A whose language contains x Final regular expression will be A A A A

Only two simplification rules Converting an NFA to a regular expression Consider the DFA for the mod 3 sum • Rule 1 Rule 1 Rule 1: For any two states q 1 and q 2 with parallel Rule 1 – Accept strings from {0,1,2}* where the digits edges (possibly q 1 =q 2 ), replace mod 3 sum of the digits is 0 A A ⋃ ⋃ ⋃ ⋃ B q 2 by q 2 q 1 q 1 0 B t 1 • Rule 2 Rule 2: Eliminate non-start/final state q 3 by Rule 2 Rule 2 1 replacing all 1 2 2 0 B 0 2 t 0 A C AB*C t 2 q 1 q 3 q 2 by q 2 q 1 1 for every pair of states q 1 , q 2 (even if q 1 =q 2 ) splicing out a node Finite automaton without t 1 Label edges with regular expressions s R 1 : 0 ∪ 10*2 ɛ ɛ ɛ ɛ R 2 : 2 ∪ 10*1 R 4 t 0 →t 1 →t 0 : 10*2 R 2 R 1 R 3 : 1 ∪ 20*2 t 0 t 2 0 t 0 →t 1 →t 2 : 10*1 R 4 : 0 ∪ 20*1 R 3 ɛ ɛ ɛ ɛ t 2 →t 1 →t 0 : 20*2 t 1 f t 2 →t 1 →t 2 : 20*1 1 s 1 s ɛ ɛ ɛ ɛ 2 2 R 5 : R 1 ∪ R 2 R 4 *R 3 ɛ ɛ ɛ ɛ 0 ɛ ɛ ɛ ɛ 0 2 R 5 t 0 t 2 t 0 f 1 ɛ ɛ ɛ ɛ f Final regular expression: (0 ∪ 10*2 ∪ (2 ∪ 10*1)(0 ∪ 20*1)*(1 ∪ 20*2))*