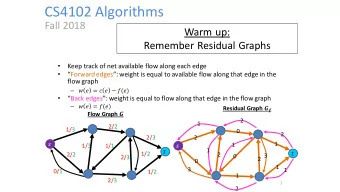
CS4102 Algorithms Fall 2020 Warm up Simplify: 1 + 2 + 3 + + ( 1) - PowerPoint PPT Presentation

CS4102 Algorithms Fall 2020 Warm up Simplify: 1 + 2 + 3 + ⋯ + (𝑜 − 1) + 𝑜 = 1

𝑜 𝑜 + 1 1 + 2 + 3 + ⋯ + (𝑜 − 1) + 𝑜 = 2 𝑜 𝑜 + 1 2

Matrix Multiplication 𝑜 1 2 3 2 4 6 𝑜 × 4 5 6 8 10 12 7 8 9 14 16 18 2 + 16 + 42 4 + 20 + 48 6 + 24 + 54 = ⋅ ⋅ ⋅ ⋅ ⋅ ⋅ 60 72 84 = 132 162 192 204 252 300 Run time? 𝑃(𝑜 3 ) 3

Matrix Multiplication D&C Multiply 𝑜 × 𝑜 matrices ( 𝐵 and 𝐶 ) Divide: 𝑏 1 𝑏 2 𝑏 3 𝑏 4 𝑐 1 𝑐 2 𝑐 3 𝑐 4 𝑏 5 𝑏 6 𝑏 7 𝑏 8 𝑐 5 𝑐 6 𝑐 7 𝑐 8 𝐵 = 𝐶 = 𝑏 9 𝑏 10 𝑏 11 𝑏 12 𝑐 9 𝑐 10 𝑐 11 𝑐 12 𝑏 13 𝑏 14 𝑏 15 𝑏 16 𝑐 13 𝑐 14 𝑐 15 𝑐 16 4

Matrix Multiplication D&C Multiply 𝑜 × 𝑜 matrices ( 𝐵 and 𝐶 ) 𝑏 1 𝑏 2 𝑏 3 𝑏 4 𝑐 1 𝑐 2 𝑐 3 𝑐 4 𝐵 1,1 𝐵 1,2 𝐶 1,1 𝐶 1,2 𝑏 5 𝑏 6 𝑏 7 𝑏 8 𝑐 5 𝑐 6 𝑐 7 𝑐 8 𝐵 = 𝐶 = 𝑏 9 𝑏 10 𝑏 11 𝑏 12 𝑐 9 𝑐 10 𝑐 11 𝑐 12 𝐵 2,1 𝐵 2,2 𝐶 2,1 𝐶 2,2 𝑏 13 𝑏 14 𝑏 15 𝑏 16 𝑐 13 𝑐 14 𝑐 15 𝑐 16 Combine: 𝐵𝐶 = 𝐵 1,1 𝐶 1,1 + 𝐵 1,2 𝐶 2,1 𝐵 1,1 𝐶 1,2 + 𝐵 1,2 𝐶 2,2 𝐵 2,1 𝐶 1,2 + 𝐵 2,2 𝐶 2,2 𝐵 2,1 𝐶 1,1 + 𝐵 2,2 𝐶 2,1 𝑈 𝑜 = 8𝑈 𝑜 2 + 4 𝑜 2 Cost of Run time? 2 additions 5

Matrix Multiplication D&C 𝑈 𝑜 = 8𝑈 𝑜 2 + 4 𝑜 2 2 𝑈 𝑜 = 8𝑈 𝑜 2 + Θ(𝑜 2 ) 𝑏 = 8, 𝑐 = 2, 𝑔 𝑜 = 𝑜 2 Case 1! 𝑜 log 𝑐 𝑏 = 𝑜 log 2 8 = 𝑜 3 𝑈 𝑜 = Θ(𝑜 3 ) We can do better… 6

Matrix Multiplication D&C Multiply 𝑜 × 𝑜 matrices ( 𝐵 and 𝐶 ) 𝑏 1 𝑏 2 𝑏 3 𝑏 4 𝑐 1 𝑐 2 𝑐 3 𝑐 4 𝐵 1,1 𝐵 1,2 𝐶 1,1 𝐶 1,2 𝑏 5 𝑏 6 𝑏 7 𝑏 8 𝑐 5 𝑐 6 𝑐 7 𝑐 8 𝐵 = 𝐶 = 𝑏 9 𝑏 10 𝑏 11 𝑏 12 𝑐 9 𝑐 10 𝑐 11 𝑐 12 𝐵 2,1 𝐵 2,2 𝐶 2,1 𝐶 2,2 𝑏 13 𝑏 14 𝑏 15 𝑏 16 𝑐 13 𝑐 14 𝑐 15 𝑐 16 𝐵𝐶 = 𝐵 1,1 𝐶 1,1 + 𝐵 1,2 𝐶 2,1 𝐵 1,1 𝐶 1,2 + 𝐵 1,2 𝐶 2,2 𝐵 2,1 𝐶 1,2 + 𝐵 2,2 𝐶 2,2 𝐵 2,1 𝐶 1,1 + 𝐵 2,2 𝐶 2,1 Idea: Use a Karatsuba-like technique on this 7

Strassen’s Algorithm Multiply 𝑜 × 𝑜 matrices ( 𝐵 and 𝐶 ) 𝑏 1 𝑏 2 𝑏 3 𝑏 4 𝑐 1 𝑐 2 𝑐 3 𝑐 4 𝐵 1,1 𝐵 1,2 𝐶 1,1 𝐶 1,2 𝑏 5 𝑏 6 𝑏 7 𝑏 8 𝑐 5 𝑐 6 𝑐 7 𝑐 8 𝐵 = 𝐶 = 𝑏 9 𝑏 10 𝑏 11 𝑏 12 𝑐 9 𝑐 10 𝑐 11 𝑐 12 𝐵 2,1 𝐵 2,2 𝐶 2,1 𝐶 2,2 𝑏 13 𝑏 14 𝑏 15 𝑏 16 𝑐 13 𝑐 14 𝑐 15 𝑐 16 Find 𝐵𝐶 : Calculate: 𝑅 1 + 𝑅 4 − 𝑅 5 + 𝑅 7 𝑅 3 + 𝑅 5 𝑅 1 = 𝐵 1,1 + 𝐵 2,2 (𝐶 1,1 + 𝐶 2,2 ) 𝑅 1 − 𝑅 2 + 𝑅 3 + 𝑅 6 𝑅 2 + 𝑅 4 𝑅 2 = 𝐵 2,1 + 𝐵 2,2 𝐶 1,1 𝑅 3 = 𝐵 1,1 (𝐶 1,2 − 𝐶 2,2 ) 𝐵 1,1 𝐶 1,1 + 𝐵 1,2 𝐶 2,1 𝐵 1,1 𝐶 1,2 + 𝐵 1,2 𝐶 2,2 𝑅 4 = 𝐵 2,2 (𝐶 2,1 − 𝐶 1,1 ) 𝐵 2,1 𝐶 1,2 + 𝐵 2,2 𝐶 2,2 𝐵 2,1 𝐶 1,1 + 𝐵 2,2 𝐶 2,1 𝑅 5 = 𝐵 1,1 + 𝐵 1,2 𝐶 2,2 𝑅 6 = 𝐵 2,1 − 𝐵 1,1 (𝐶 1,1 + 𝐶 1,2 ) Number Mults.: 7 Number Adds.: 18 𝑈 𝑜 = 7𝑈 𝑜 2 + 9 𝑅 7 = 𝐵 1,2 − 𝐵 2,2 (𝐶 2,1 + 𝐶 2,2 ) 2 𝑜 2 8

Strassen’s Algorithm 𝑈 𝑜 = 7𝑈 𝑜 2 + 9 2 𝑜 2 𝑏 = 7, 𝑐 = 2, 𝑔 𝑜 = 9 2 𝑜 2 Case 1! 𝑜 log 𝑐 𝑏 = 𝑜 log 2 7 ≈ 𝑜 2.807 𝑈 𝑜 = Θ 𝑜 log 2 7 ≈ Θ(𝑜 2.807 ) 9

Strassen’s Algorithm 𝑜 3 𝑜 log 2 7 10

Is this the fastest? Best possible is unknown May not even exist! 11

Recurrence Solving Techniques Tree ? Guess/Check “ Cookbook ” Substitution 12

Observation • Divide: 𝐸(𝑜) time, • Conquer: recurse on small problems, size 𝑡 • Combine: C(𝑜) time • Recurrence: 𝑈 𝑜 = 𝐸 𝑜 + 𝑈(𝑡) + 𝐷(𝑜) • Many D&C recurrences are of form: 𝑈 𝑜 = 𝑏𝑈 𝑜 𝑐 + 𝑔(𝑜) 13

Master Theorem 𝑈 𝑜 = 𝑏𝑈 𝑜 𝑐 + 𝑔(𝑜) • Case 1: if 𝑔 𝑜 = 𝑃(𝑜 log 𝑐 𝑏 −𝜁 ) for some constant 𝜁 > 0 , then 𝑈 𝑜 = Θ(𝑜 log 𝑐 𝑏 ) • Case 2: if 𝑔 𝑜 = Θ(𝑜 log 𝑐 𝑏 ) , then 𝑈 𝑜 = Θ(𝑜 log 𝑐 𝑏 log 𝑜) • Case 3: if 𝑔 𝑜 = Ω(𝑜 log 𝑐 𝑏+𝜁 ) for some constant 𝜁 > 0 , and if 𝑜 𝑏𝑔 ≤ 𝑑𝑔(𝑜) for some constant 𝑑 < 1 and all sufficiently large 𝑐 𝑜 , then 𝑈 𝑜 = Θ(𝑔 𝑜 ) 14

Substitution Method • Idea: take a “difficult” recurrence, re -express it such that one of our other methods applies. • Example: 𝑈 𝑜 = 2𝑈 𝑜 + log 2 𝑜 15

Tree method log 2 𝑜 1/2 = 1 2 log 2 𝑜 𝑈 𝑜 = 2𝑈( 𝑜) + log 2 𝑜 log 2 𝑜 log 2 𝑜 𝑜 1 1 log 2 𝑜 𝑜 𝑜 + 2 log 2 𝑜 2 log 2 𝑜 1 log 2 log 2 𝑜 1 1 1 4 log 2 𝑜 4 log 2 𝑜 4 log 2 𝑜 4 log 2 𝑜 log 2 𝑜 + + + 𝑜 𝑜 𝑜 𝑜 … … … … 2 … 1 1 1 1 1 1 log 2 𝑜 2 2 2 2 2 + + + + + 𝑈 𝑜 = 𝑃(log 2 𝑜 ⋅ log 2 log 2 𝑜) 16

Substitution Method 𝑈 𝑜 = 2𝑈 𝑜 + log 2 𝑜 I don’t like the ½ in 𝑈 𝑜 = 2𝑈 𝑜 1/2 + log 2 𝑜 the exponent Let 𝑜 = 2 𝑛 , i.e. 𝑛 = log 2 𝑜 Now the variable is in the exponent on both sides! 𝑛 𝑈 2 𝑛 = 2𝑈 2 + 𝑛 Rewrite in terms of exponent! 2 𝑛 Let 𝑇 𝑛 = 2𝑇 + 𝑛 S will operate exactly as T, just Case 2! 2 redefined in terms of the exponent Let 𝑇 𝑛 = Θ(𝑛 log 𝑛) Substitute Back 𝑇 𝑛 = 𝑈(2 𝑛 ) Let T 𝑜 = Θ(log 𝑜 log log 𝑜) 17

Tree method 𝑛 𝑈 2 𝑛 = 2𝑈 2 𝑈 𝑜 = 2𝑈( 𝑜) + log 2 𝑜 𝑜 = 2 𝑛 + 𝑛 2 log 2 𝑜 log 2 𝑜 𝑜 2 𝑛 1 1 log 2 𝑜 𝑜 𝑜 + 2 log 2 𝑜 2 𝑛/2 2 log 2 𝑜 2 𝑛/2 1 1 1 1 4 log 2 𝑜 4 log 2 𝑜 4 log 2 𝑜 log 2 log 2 𝑜 4 log 2 𝑜 log 2 𝑜 + + + 2 𝑛/4 2 𝑛/4 2 𝑛/4 2 𝑛/4 𝑜 𝑜 𝑜 𝑜 … … … … 2 … 1 1 1 1 1 1 log 2 𝑜 2 2 2 2 2 + + + + + 18

Tree method 𝑜 = 2 𝑛 𝑈 2 𝑛 = 2𝑈(2 𝑛/2 ) + 𝑛 𝑛 𝑛 2 𝑛 𝑛 𝑛 2 𝑛/2 2 𝑛/2 𝑛 + 2 2 log 2 𝑛 𝑛 𝑛 𝑛 𝑛 𝑛 + + 2 𝑛/4 4 2 𝑛/4 4 2 𝑛/4 4 2 𝑛/4 4 + … … … … 2 1 … 1 1 1 1 1 1 2 1 2 1 2 1 2 1 2 1 𝑛 + + + + + 19

Tree method 𝑇 𝑛 = 2𝑇 𝑛 𝑜 = 2 𝑛 + 𝑛 𝑈 2 𝑛 = 𝑇(𝑛) 2 𝑛 𝑛 𝑛 𝑛 𝑛 𝑛 𝑛/2 𝑛/2 + 2 2 log 2 𝑛 𝑛 𝑛 𝑛 𝑛 𝑛 + + 4 4 4 4 + 𝑛/4 𝑛/4 𝑛/4 𝑛/4 … … … … 1 … 1 1 1 1 1 1 𝑛 1 1 1 1 1 + + + + + 𝑈 𝑜 = 𝑃(𝑛 ⋅ log 2 𝑛) = 𝑃(log 2 𝑜 ⋅ log 2 log 2 𝑜) 20