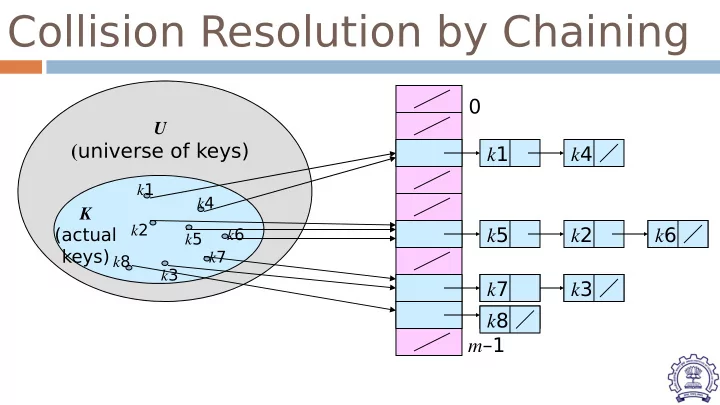
Collision Resolution by Chaining 0 U ( universe of keys) k 1 k 4 k - PowerPoint PPT Presentation

Collision Resolution by Chaining 0 U ( universe of keys) k 1 k 4 k 1 k 4 K k 2 k 5 k 2 k 6 (actual k 6 k 5 keys) k 7 k 8 k 3 k 7 k 3 k 8 m –1

Expected Cost of an Search Theorem: An unsuccessful search takes expected time Θ(1+α). Proof Idea: T o search unsuccessfully for any key k , need to search to the end of the list T [ h ( k )], and E[ T [ h ( k )]] = α. Theorem: A successful search takes expected time Θ(1+α). Proof Idea: T o search successfully, calculate probability that key i collides with j and j was inserted before i . Average over all n keys.

Open Addressing  If we have enough contiguous memory to store all the keys (m > n) ⇒ store the keys in the table itself  No need to use linked lists anymore  Basic idea: Insertion: if a slot is full, try another one, until you find an empty one  Search: follow the same sequence of probes  Deletion: more difficult, we will see later   Search time depends on the length of the probe sequence! 3

Linear Probing – Get And Put  Let m = 17 and h(k) = k % 17. 0 4 8 12 16 34 0 45 6 23 7 2 1 2 1 3 3 8 2 9 1 0 3 • Put in pairs whose keys are 6, 12, 34, 29, 28, 11, 23, 7, 0, 33, 30, 45

Useful way to think about probing  Let h(k) be the hash function used  When a collision occurs, try a different table cell.  Try in succession h 0( x ), h 1( x ), h 2( x ), ...  hi ( x ) = ( h ( x ) + f ( i )) mod m , with f (0) = 0  i = 0, 1, 2, …, m-1  Function f is the collision resolution strategy.  With linear probing, f is a linear function of i , typically, f ( i ) = i

Clustering Problem  As long as table is big enough, a free cell can always be found, but the time to do so can get quite large.  Worse, even if the table is relatively empty, blocks of occupied cells start forming.  This effect is known as primary clustering .  Any key that hashes into the cluster will require several attempts to resolve the collision, and then it will add to the cluster. CENG 213 Data Structures

Revisit the Example 7  Let m = 17 and h(k) = k % 17. 0 4 8 12 16 34 0 6 23 7 2 1 2 1 3 3 8 2 9 1 0 3 • Put in pairs whose keys are 6, 12, 34, 29, 28, 11, 23, 7, 0, 33, 30 • Consider what happens when we insert 45

Performance Of Linear Probing 0 4 8 12 16 34 0 45 6 23 7 28 12 29 11 30 33  Worst-case get/put time is O(n), where n is the number of pairs in the table.  This happens when all pairs are in the same cluster.

Expected Performance 0 4 8 12 16 34 0 45 6 23 7 28 12 29 11 30 33  alpha = loading density = number of pairs/slots = n/m.  alpha = 12/17 .  Sn = expected number of buckets examined in a successful search when n is large  Un = expected number of buckets examined in a unsuccessful search when n is large  Time to put governed by Un.

Expected Performance  Sn ~ ½(1 + 1/(1 – alpha))  Un ~ ½(1 + 1/(1 – alpha)2)  Note that 0 <= alpha <= 1 alpha S U n n 0.50 1.5 2.5 Alpha <= 0.75 is 0.75 2.5 8.5 recommended. 0.90 5.5 50.5

Hash T able Design  Performance requirements are given, determine maximum permissible loading density.  We want a successful search to make no more than 10 compares (expected).  Sn ~ ½(1 + 1/(1 – alpha))  alpha <= 18/19  We want an unsuccessful search to make no more than 13 compares (expected).  Un ~ ½(1 + 1/(1 – alpha)2)  alpha <= 4/5  So alpha <= min{18/19, 4/5} = 4/5.

Quadratic Probing  Quadratic Probing eliminates primary clustering problem of linear probing.  Collision function is quadratic.  The popular choice is f(i) = i2 .  If the hash function evaluates to h and a search in cell h is inconclusive, we try cells h + 12, h+22, … h + i2.  i.e. It examines cells 1,4,9 and so on away from the original probe.  Remember that subsequent probe points are a quadratic number of positions from the original probe point .

Homework  Let m = 17 and h(k) = k % 17.  Put in pairs whose keys are 6, 12, 34, 29, 28, 11, 23, 7, 0, 33, 30, 45  Homework:  Find average length of probe if linear probe is used  Perform quadratic probing with f(i) = i2  List the positions of all the keys  Find the average length of probe if quadratic probe is used

Hash T able Design  Dynamic resizing of table.  Whenever loading density exceeds threshold (4/5 in our example), rehash into a table of approximately twice the current size.

Nature Lover’s View of A Tree leaves branches root

Computer Scientist’s View root leaves branches nodes

Linear Lists And Trees  Linear lists are useful for serially ordered data.  (e0, e1, e2, …, en-1)  Days of week.  Months in a year.  Students in this class.  Trees are useful for hierarchically ordered data.  Employees of a corporation.  President, vice presidents, managers, and so on.  Java ’ s classes.  Object is at the top of the hierarchy.  Subclasses of Object are next, and so on.

Hierarchical Data And Trees  The element at the top of the hierarchy is the root.  Elements next in the hierarchy are the children of the root.  Elements next in the hierarchy are the and children of the root, and so on.  Elements that have no children are leaves.

Definition  A tree t is a finite nonempty set of elements.  One of these elements is called the root.  The remaining elements, if any, are partitioned into trees, which are called the subtrees of t.

Caution  Some texts start level numbers at 0 rather than at 1.  Root is at level 0.  Its children are at level 1.  The grand children of the root are at level 2.  And so on.  We shall number levels with the root at level 1.

height = depth = number of levels Object OutputStream Number Throwable FileOutputStream Integer Double Exception Level 3 RuntimeException Level 4

Node Degree = Number Of Children 3 Object OutputStream 2 Number 1 Throwable 1 0 0 1 0 FileOutputStream Integer Double Exception 0 RuntimeException

Tree Degree = Max Node Degree Object 3 OutputStream 2 1 1 Number Throwable 0 0 1 0 FileOutputStream Integer Double Exception RuntimeException 0 Degree of tree = 3.

Binary Tree  Finite (possibly empty) collection of elements.  A nonempty binary tree has a root element.  The remaining elements (if any) are partitioned into two binary trees.  These are called the left and right subtrees of the binary tree.

Differences Between A Tree & A Binary Tree  No node in a binary tree may have a degree more than 2, whereas there is no limit on the degree of a node in a tree.  A binary tree may be empty; a tree cannot be empty.

Differences Between A Tree & A Binary Tree  The subtrees of a binary tree are ordered; those of a tree are not ordered. a a b b • Are different when viewed as binary trees. • Are the same when viewed as trees.

Arithmetic Expressions  (a + b) * (c + d) + e – f/g*h + 3.25  Expressions comprise three kinds of entities.  Operators (+, -, /, *).  Operands (a, b, c, d, e, f, g, h, 3.25, (a + b), (c + d), etc.).  Delimiters ((, )).

Binary Tree Properties & Representation

Minimum Number Of Nodes  Minimum number of nodes in a binary tree whose height is h.  At least one node at each of first h levels. minimum number of nodes is h

Maximum Number Of Nodes  All possible nodes at first h levels are present. Maximum number of nodes = 1 + 2 + 4 + 8 + … + 2h-1 = 2h - 1

Number Of Nodes & Height  Let n be the number of nodes in a binary tree whose height is h.  h <= n <= 2h – 1  log2(n+1) <= h <= n

Full Binary Tree  A full binary tree of a given height h has 2h – 1 nodes. Height 4 full binary tree.

Numbering Nodes In A Full Binary Tree  Number the nodes 1 through 2h – 1.  Number by levels from top to bottom.  Within a level number from left to right. 1 2 3 4 6 5 7 8 9 10 11 12 13 14 15