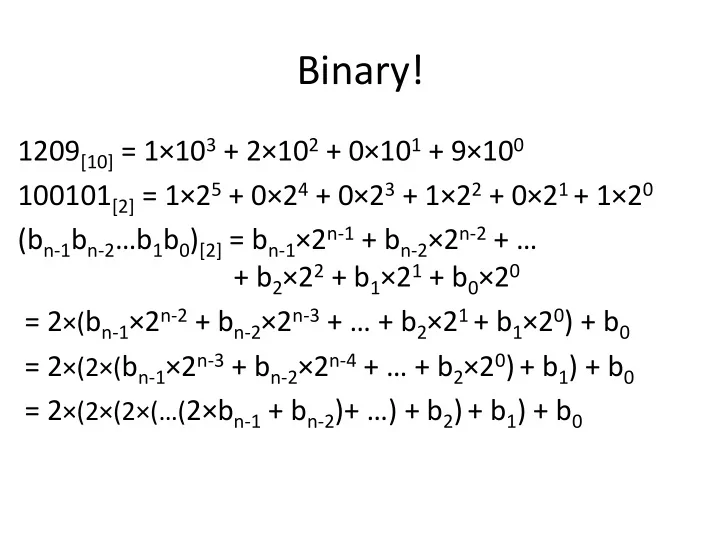
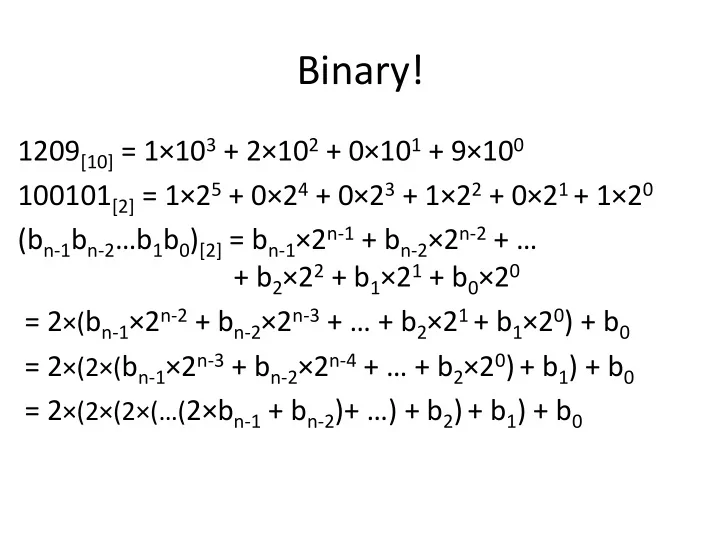
Binary! 1209 [10] = 110 3 + 210 2 + 010 1 + 910 0 100101 - PowerPoint PPT Presentation

Binary! ¡ 1209 [10] ¡= ¡1×10 3 ¡+ ¡2×10 2 ¡+ ¡0×10 1 ¡+ ¡9×10 0 ¡ 100101 [2] ¡= ¡1×2 5 ¡+ ¡0×2 4 ¡+ ¡0×2 3 ¡+ ¡1×2 2 ¡+ ¡0×2 1 ¡ + ¡1×2 0 ¡ (b n-­‑1 b n-­‑2 …b 1 b 0 ) [2] ¡= ¡b n-­‑1 ×2 n-­‑1 ¡+ ¡b n-­‑2 ×2 n-­‑2 ¡+ ¡… ¡ ¡ ¡ ¡ ¡ ¡ ¡+ ¡b 2 ×2 2 ¡+ ¡b 1 ×2 1 ¡+ ¡b 0 ×2 0 ¡ ¡= ¡2 ×( b n-­‑1 ×2 n-­‑2 ¡+ ¡b n-­‑2 ×2 n-­‑3 ¡+ ¡… ¡+ ¡b 2 ×2 1 ¡ + ¡b 1 ×2 0 ) ¡+ ¡b 0 ¡ ¡= ¡2 ×(2×( b n-­‑1 ×2 n-­‑3 ¡+ ¡b n-­‑2 ×2 n-­‑4 ¡+ ¡… ¡+ ¡b 2 ×2 0 ) ¡ + ¡b 1 ) ¡+ ¡b 0 ¡ ¡= ¡2 ×(2×(2×(…( 2×b n-­‑1 ¡+ ¡b n-­‑2 )+ ¡…) ¡+ ¡b 2 ) ¡ + ¡b 1 ) ¡+ ¡b 0 ¡ ¡

Hexadecimal! ¡ • 0 [16] ¡0000 [2] ¡0 [10] ¡ • 8 [16] ¡1000 [2] ¡8 [10] ¡ ¡ ¡ ¡ • 1 [16] ¡0001 [2] ¡1 [10] ¡ • 9 [16] ¡1001 [2] ¡9 [10] ¡ ¡ ¡ ¡ • 2 [16] ¡0010 [2] ¡2 [10] ¡ • A [16] ¡ ¡1010 [2] ¡10 [10] ¡ ¡ ¡ ¡ • 3 [16] ¡0011 [2] ¡3 [10] ¡ • B [16] ¡ ¡1011 [2] ¡11 [10] ¡ ¡ ¡ ¡ • 4 [16] ¡0100 [2] ¡4 [10] ¡ • C [16] ¡ ¡1100 [2] ¡12 [10] ¡ ¡ ¡ ¡ • 5 [16] ¡0101 [2] ¡5 [10] ¡ • D [16] ¡ ¡1101 [2] ¡13 [10] ¡ ¡ ¡ ¡ • 6 [16] ¡0110 [2] ¡6 [10] ¡ • E [16] ¡1110 [2] ¡14 [10] ¡ ¡ ¡ ¡ • 7 [16] ¡0111 [2] ¡7 [10] ¡ • F [16] ¡ ¡1111 [2] ¡15 [10] ¡ ¡ ¡ ¡ ¡

Hexadecimal! ¡ 0*16 + C = 12 12*16 + 0 = 192 192*16 + F = 3087 3087*16 + A = 49402 49402*16 + C = 790444 790444*16 + E = 12647119

Hexadecimal! ¡ 0*16 + C = 12 12*16 + 0 = 192 192*16 + F = 3087 3087*16 + A = 49402 49402*16 + C = 790444 790444*16 + E = 12647119 --> 0xC0FACE 12647118 (int) --> int2hex(12647118); "00C0FACE" (string)

Modular ¡arithmeNc ¡ 11 1 1 01101010 (106) 01101010 (106) + 10101010 (170) x 10101010 (170) 100010100 (276) 00000000 01101010 00000000 01101010 00000000 01101010 00000000 + 01101010 100011001100100 (18020)

Modular ¡arithmeNc ¡ 11 1 1 01101010 (106) 01101010 (106) + 10101010 (170) x 10101010 (170) 100010100 (276) 00000000 01101010 00010100 (20) 00000000 01101010 00000000 01101010 00000000 + 01101010 100011001100100 (18020) 01100100 (100)

0000 1111 0001 1110 0010 1101 0011 1100 0100 1011 0101 1010 0110 1001 0111 1000

0000 1111 0001 ¡ 15 ¡ 0 ¡ ¡ 1110 0010 1 ¡ ¡ 14 ¡ ¡ ¡ ¡2 ¡ ¡ 13 ¡ 1101 0011 3 ¡ ¡ Unsigned ¡ 4 ¡ 12 ¡ 1100 0100 ¡ ¡ 5 ¡ 11 ¡ ¡ 1011 0101 ¡ 6 ¡ 10 ¡ ¡ ¡ 7 ¡ 1010 0110 9 ¡ ¡ ¡ 8 ¡ ¡ 1001 0111 1000

0000 1111 0001 16 ¡ 15 ¡ 0 ¡ 17 ¡ 1110 0010 -­‑1 ¡ 1 ¡ 18… ¡ 14 ¡ ¡ ¡ ¡2 ¡ -­‑2 ¡ …-­‑14 ¡ 13 ¡ 1101 0011 3 ¡ -­‑3 ¡ -­‑13 ¡ Unsigned ¡ 4 ¡ 12 ¡ 1100 0100 -­‑12 ¡ -­‑4 ¡ 5 ¡ 11 ¡ -­‑11 ¡ 1011 0101 -­‑5 ¡ 6 ¡ 10 ¡ -­‑10 ¡ -­‑6 ¡ 7 ¡ 1010 0110 9 ¡ -­‑9 ¡ -­‑7 ¡ 8 ¡ -­‑8 ¡ 1001 0111 1000

0000 1111 0001 16 ¡ 15 ¡ 0 ¡ 17 ¡ 1110 0010 -­‑1 ¡ 1 ¡ 18… ¡ 14 ¡ ¡ ¡ ¡2 ¡ -­‑2 ¡ …-­‑14 ¡ 13 ¡ 1101 0011 3 ¡ -­‑3 ¡ -­‑13 ¡ 4 ¡ 12 ¡ 1100 0100 -­‑12 ¡ -­‑4 ¡ 5 ¡ 11 ¡ -­‑11 ¡ 1011 0101 -­‑5 ¡ 6 ¡ 10 ¡ -­‑10 ¡ -­‑6 ¡ 7 ¡ 1010 0110 9 ¡ -­‑9 ¡ -­‑7 ¡ 8 ¡ -­‑8 ¡ 1001 0111 1000

0000 1111 0001 16 ¡ 15 ¡ 0 ¡ 17 ¡ 1110 0010 -­‑1 ¡ 1 ¡ 18… ¡ 14 ¡ ¡ ¡ ¡2 ¡ -­‑2 ¡ …-­‑14 ¡ 13 ¡ 1101 0011 3 ¡ -­‑3 ¡ -­‑13 ¡ 4 ¡ 12 ¡ 1100 0100 -­‑12 ¡ -­‑4 ¡ 5 ¡ 11 ¡ -­‑11 ¡ 1011 0101 -­‑5 ¡ 6 ¡ 10 ¡ -­‑10 ¡ -­‑6 ¡ 7 ¡ 1010 0110 9 ¡ -­‑9 ¡ -­‑7 ¡ 8 ¡ -­‑8 ¡ 1001 0111 1000

0000 1111 0001 16 ¡ 15 ¡ 0 ¡ 17 ¡ 1110 0010 -­‑1 ¡ 1 ¡ 18… ¡ 14 ¡ ¡ ¡ ¡2 ¡ -­‑2 ¡ …-­‑14 ¡ 13 ¡ 1101 0011 3 ¡ -­‑3 ¡ -­‑13 ¡ 4 ¡ 12 ¡ 1100 0100 -­‑12 ¡ -­‑4 ¡ 5 ¡ 11 ¡ -­‑11 ¡ 1011 0101 -­‑5 ¡ 6 ¡ 10 ¡ -­‑10 ¡ -­‑6 ¡ 7 ¡ 1010 0110 9 ¡ -­‑9 ¡ -­‑7 ¡ 8 ¡ -­‑8 ¡ 1001 0111 1000

0000 1111 0001 16 ¡ 15 ¡ 0 ¡ 17 ¡ 1110 0010 -­‑1 ¡ 1 ¡ 18… ¡ 14 ¡ ¡ ¡ ¡2 ¡ -­‑2 ¡ …-­‑14 ¡ 13 ¡ 1101 0011 3 ¡ -­‑3 ¡ -­‑13 ¡ Two’s ¡ 4 ¡ 12 ¡ 1100 0100 -­‑12 ¡ Complement ¡ -­‑4 ¡ 5 ¡ 11 ¡ -­‑11 ¡ 1011 0101 -­‑5 ¡ 6 ¡ 10 ¡ -­‑10 ¡ -­‑6 ¡ 7 ¡ 1010 0110 9 ¡ -­‑9 ¡ -­‑7 ¡ 8 ¡ -­‑8 ¡ 1001 0111 1000

Addi>ve ¡inverse: ¡ -x 0000 1111 0001 1110 0010 1101 0011 1100 0100 1011 0101 1010 0110 1001 0111 -x + x = 0_ 1000

0000 Bitwise ¡nega>on: ¡ ~x 1111 0001 1110 0010 1101 0011 1100 0100 1011 0101 1010 0110 1001 0111 ~x + x = -1 1000 ~x | x = -1

Addi>ve ¡inverse: ¡ -x 0000 Bitwise ¡nega>on: ¡ ~x 1111 0001 1110 0010 1101 0011 1100 0100 1011 0101 1010 0110 1001 0111 ~x + x = -1 1000 ~x + 1 = -x